Onderstaand doolhof komt uit Geen doolhoven voor domoren, de Nederlandse vertaling van Mad mazes (1990), door Robbert Abbott. In dit boekje staan twintig verschillende doolhofpuzzels. Dit doolhof, 'Doolhof 8', noem ik het 'pijlendoolhof'. Bij figuur 1 hoort de (door mij enigszins aangepaste) opgave 1. 

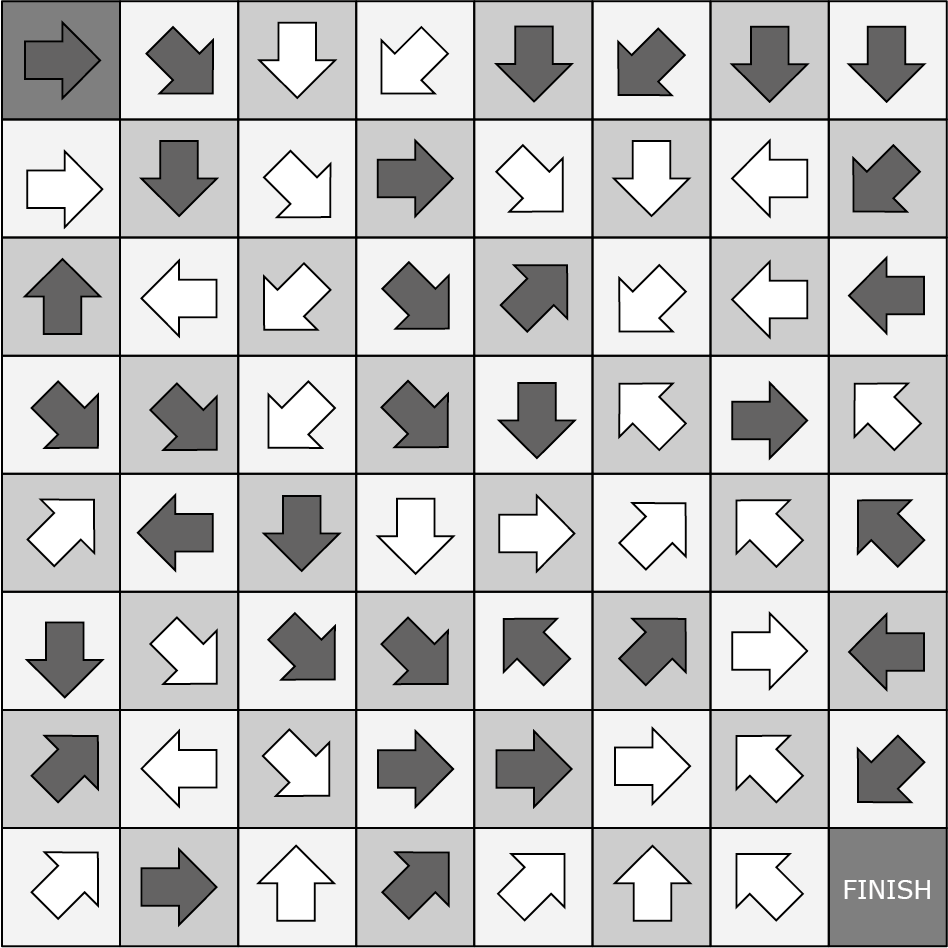
Opgave 1 Begin op de donkere pijl in de linkerbovenhoek. Deze pijl wijst naar twee lichte pijlen. Hiervan kies je er een; ga naar dat veld. De lichte pijl waar je nu op staat wijst op zijn beurt weer naar een of meer donkere pijlen. Kies een van deze donkere pijlen en ga naar dat veld. Op deze wijze ga je door, donkere en lichte pijlen afwisselend, totdat je op een pijl komt die je naar FINISH (rechts onder) wijst.

Via de knop [Bekijk oplossing] kom je bij de oplossing van dit pijlendoolhof. Geen gemakkelijke route (en erg lang, naar mijn idee). Maar waarom zouden we de pijlen en het ingewikkelde 'van licht naar donker en omgekeerd' kiezen van de pijlen niet vervangen door eenvoudige codes voor de acht richtingen noord, noordoost, oost et cetera? In figuur 2 zijn deze acht richtingen vervangen door de getallen 1 tot en met 8.

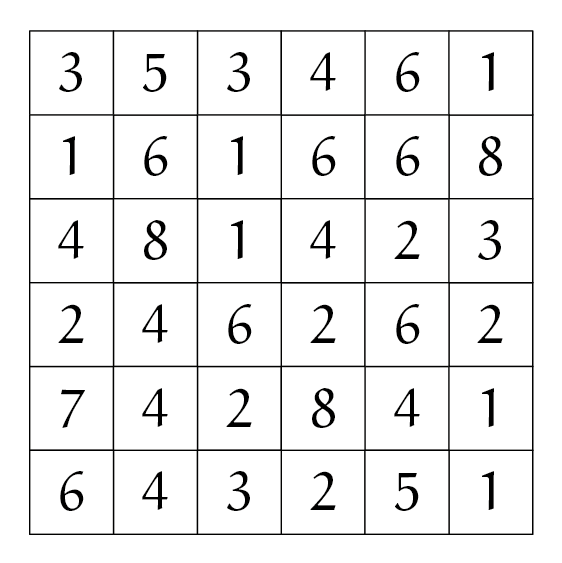
Nu kunnen we een leuk (en redelijk eenvoudig − het gaat tenslotte om het idee) doolhof introduceren: het 'codedoolhof'. We gaan in onderstaand codedoolhof steeds één veld horizontaal, verticaal of diagonaal. De opdracht is alleen misschien anders dan je wellicht gewend bent. In bovenstaand codedoolhof is er één route (van begin naar eind) met het grootste aantal stappen.

Opgave 2 Bepaal waar dit codedoolhof begint en waar eindigt.

Als deze puzzel je bevalt, heb ik nog een vervolg voor je. De bovenstaande vraag ging over de 'éénstapsvariant': er mocht maar één stap horizontaal, verticaal of diagonaal gedaan worden (zoals bijvoorbeeld de koning van het schaakspel loopt). Maar wat is de kortste route van het codedoolhof uit opgave 2 als we meerdere stappen in een richting toestaan (zoals bij het pijlendoolhof uit het voorbeeld, of zoals de dame van het schaakspel beweegt)? Ik noem dit de 'meerstapsvariant'.

Opgave 3 Zoek de kortste route in het codedoolhof bij de 'meerstapsvariant'.

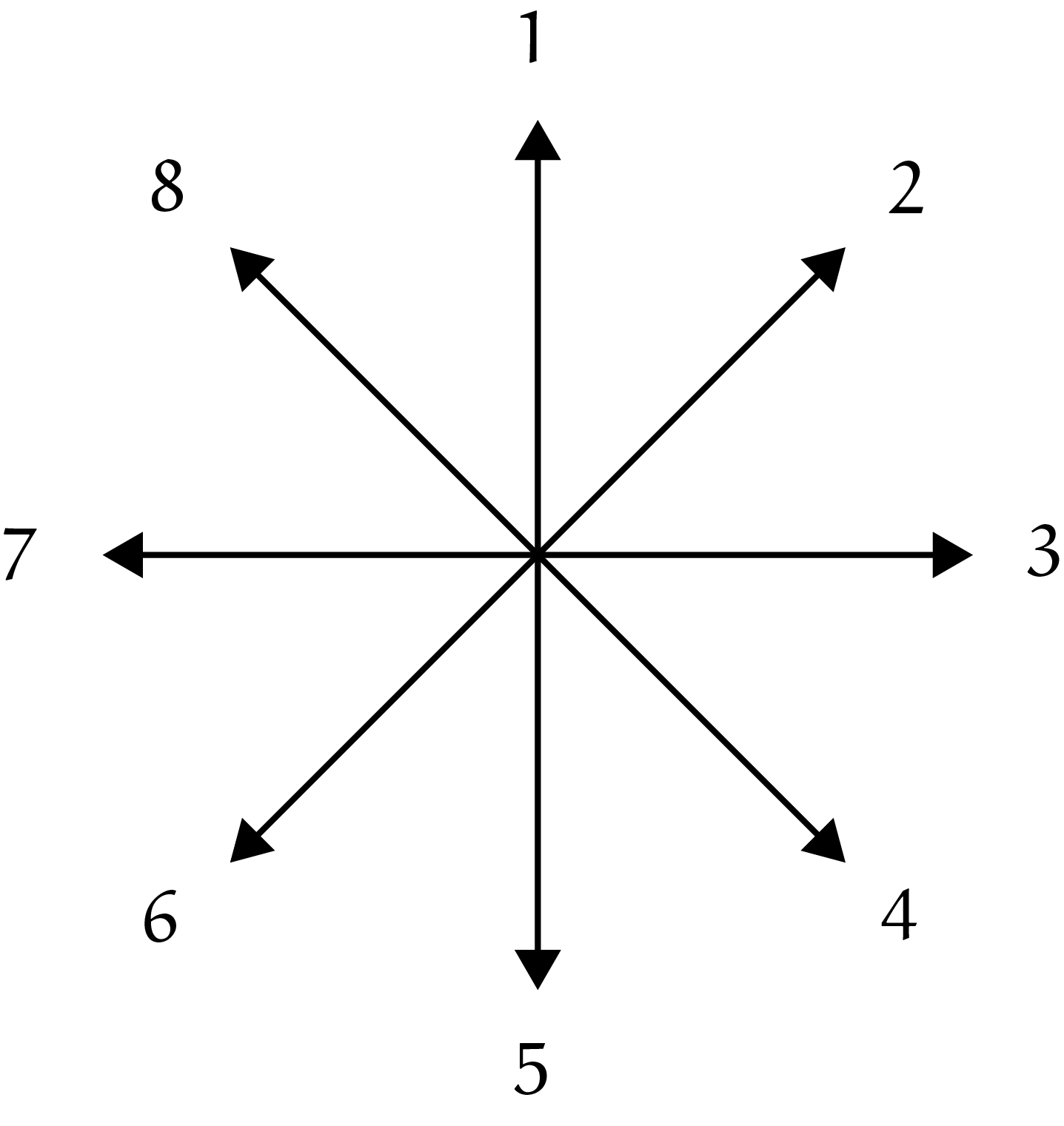
In plaats van het codedoolhof met acht richtingen uit de vorige puzzel, introduceer ik hier als variant een (veel gemakkelijker?) drierichtingendoolhof. Ook nu weer gaan we telkens één stap, horizontaal of verticaal, afhankelijk van een code voor een richting, maar nu niet diagonaal. We gaan uit van de codes 1, 2, 3 en 4 op de volgende manier, uitgaande van de richting waarin men al bewoog (zie figuur 4):

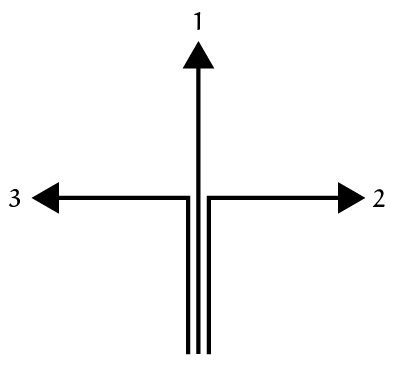
1. Ga rechtdoor
2. Ga rechtsaf
3. Ga linksaf
4. Vrije keuze voor rechtdoor, rechtsaf of linksaf

De start van dit doolhof in figuur 5 is linksonder; rechtsboven is de 'Finish'. Let op: het maakt in dit doolhof natuurlijk uit in welke richting je je beweegt om uit te maken naar welk volgend veld je mag. Ga je vanuit het startveld met code '4' een veld omhoog, dan moet je daarna rechtdoor (veld met code '1') en daarna rechtsaf (veld met een '2'), et cetera. (Omdat het startveld code '4' heeft, mag je zelf een richting kiezen: 'omhoog' of 'naar rechts'. Als het startveld een code 1, 2 of 3 had gehad, was een richtingsaanduiding nodig geweest.)

Opgave 4 Zoek de kortste route in dit 'drierichtingendoolhof'.

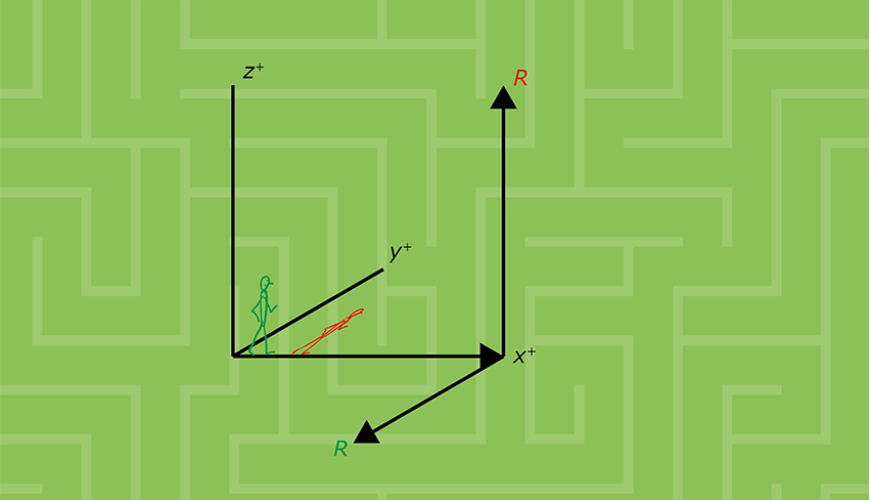
Als er een tweedimensionaal codedoolhof (zie Opgave 4) met codes voor linksaf, rechtsaf et cetera bestaat, kunnen we natuurlijk ook een '3D-codedoolhof' maken! Dat doen we met behulp van het assenstelsel in figuur 6, met positieve $x$-, $y$- en $z$-as. De positieve $y$-as verdwijnt hierbij 'loodrecht het papier in'.

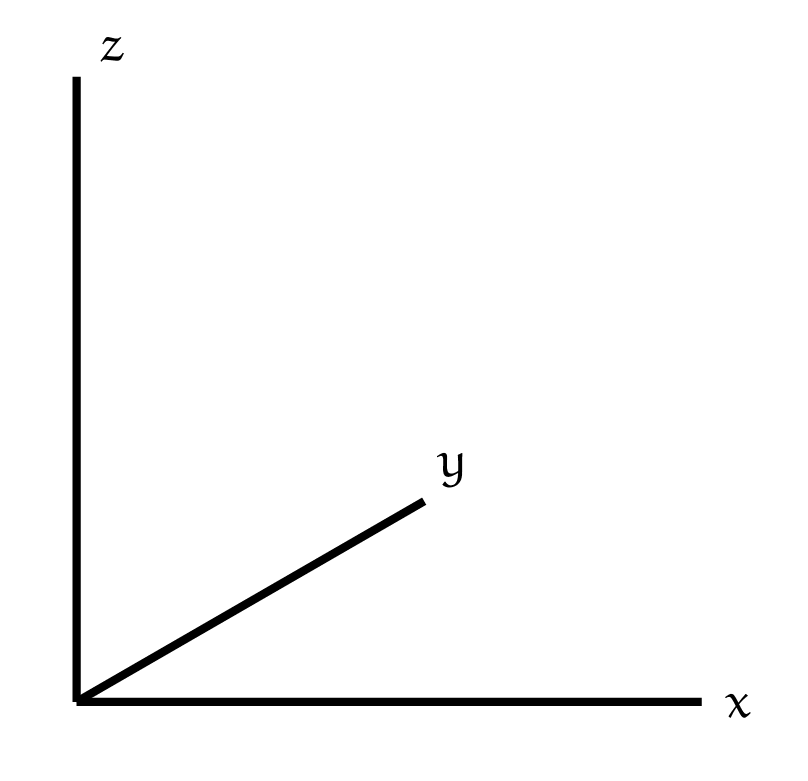
Er is echter een probleem: de definities van linksaf en rechtsaf zijn niet eenduidig! Sterker: er zijn nog twee andere 'richtingen' mogelijk: 'omhoog' en 'omlaag', en die zijn ook niet uniek vast te leggen. Ga maar na: als je in positieve $x$-richting ($x+$) beweegt, kun je 'rechtsaf' ($R$) in het $xy$-vlak beschouwen als het in negatieve $y$-richting gaan ('$y-$-richting'); zie figuur 7. Maar je kunt een $x+$-beweging ook opvatten in het $xz$-vlak, en dan is 'rechtsaf' naar 'boven' ('$z+$-richting') in de figuur (je hoofd zit 'achter' het papier)!

Dat is natuurlijk verwarrend – en dat geldt ook voor de beweegrichtingen $y$ en $z$. We gaan daarom uit van andere codes dan in de vorige puzzel. Deze codes kiezen we nu onafhankelijk van de richting waaruit we kwamen. We definiëren in een willekeurig veld:

Ga één hokje verder in:

1. $x+$-richting
2. $x-$-richting
3. $y+$-richting
4. $y-$-richting
5. $z+$-richting
6. $z-$-richting
7. een zelfgekozen $1$ t/m $6$

Code '7' betekent dus een vrije keuze van een van de zes richtingen. NB: 'terug' mag dan dus ook! De start van dit doolhof is weer linksonder; de 'finish' $F$ is 'rechtsachter, boven'. Verder moeten we steeds binnen de kubus blijven, maar dat spreekt eigenlijk voor zich, want buiten de kubus zijn er geen codes, dus richtingen bekend.

Opgave 5 Vind de kortste route in dit '3D-codedoolhof'.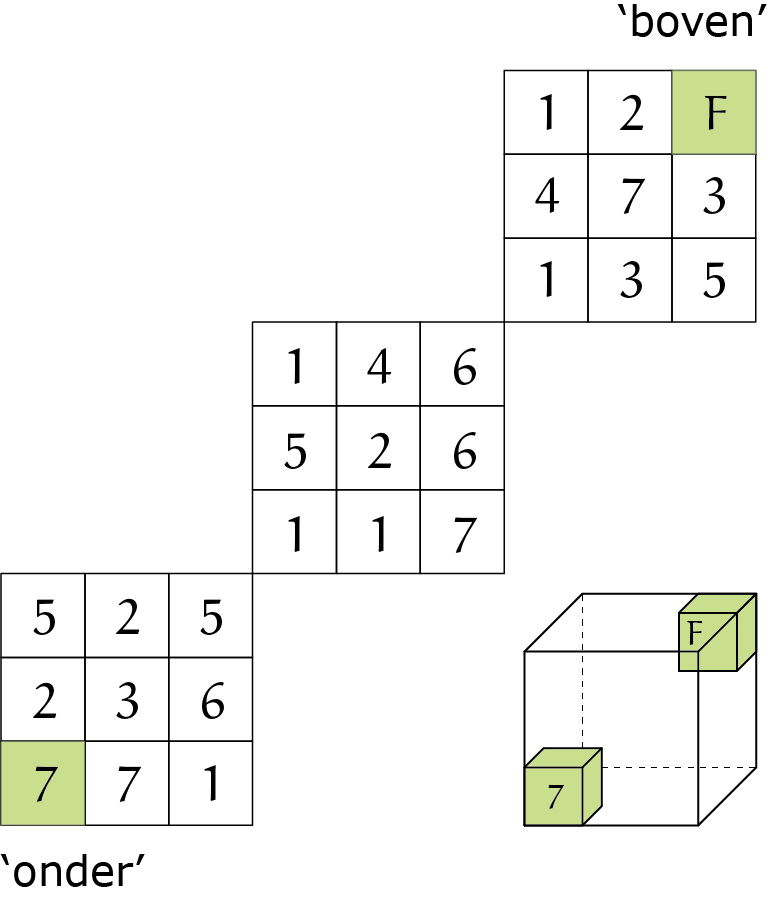

 

De opgaven 2 tot en met 5 zijn onlangs gepubliceerd als puzzels in Denkstof, New Scientist (2024). Wil je nog meer puzzelen? We mogen 3 exemplaren van Denkstof weggeven. Stuur een email met je naam en adresgegevens voor 15 januari 2025 naar [email protected] om kans te maken op een exemplaar!

 

Bekijk oplossing