Opgave 1

Voor het pijlendoolhof is, in schaaknotatie ($a1$ linksonder; $h8$ is rechtsboven), de enig  mogelijke route van 25 (!) zetten:

$a8-c8-c3-c2-d1-g4-d7-g7-b7-b6-a6-a7-h7\cdots$
$\cdots g6-d6-f4-h6-c6-b5-f1-f8-c5-a3-a1-h8-h1$.

Je kunt hierbij bijvoorbeeld gebruik maken van ‘backtracking’. Kies een route zolang dat kan. Loop je vast, ga dan in de laatste zet na of er een zet mogelijke is. Zo ja, kies dan die zet. Zo nee, ga nog een zet terug en kijk of daar een andere voortzetting mogelijk is, enzovoort. 

Opgave 2

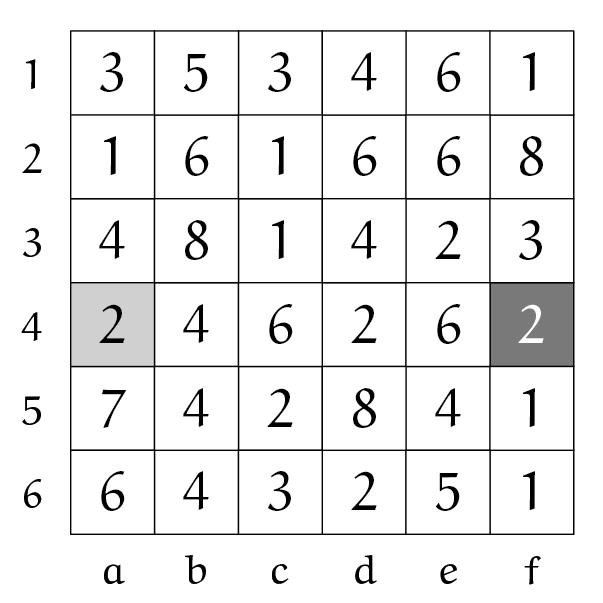
Op zes velden na (in schaaknotatie $a1, a2, b1, e1, f4$ en $f6$) zijn alle andere 30 velden in één richting met elkaar verbonden met als beginveld $a3$ (donkere veld met zwarte $2$) en eindveld $f3$ (donkere veld met witte $2$). Dat pad is: $a3-b4-a5-a6-b6$ et cetera. In strikte zin is de éénstapsvariant geen echt doolhof, want er is maar één weg van begin naar einde…

Opgave 3

Bij deze meerstapsvariant van opgave 2 ontstaat wel een echt achtrichtingendoolhof. De kortste route (in aantal stappen én lengte) is: $a3-d6-e5-d4-f2-f3$.

Opgave 4

In schaaknotatie van de 36 velden  is de kortste route:

$a1-b1-c1-d1-d2-d3-d4-d5-d6-c6-c5-d5\cdots$
$\cdots e5-e4-d4-c4-c3-d3-e3-f3-f4-f5-e5-e6-f6$.

NB: er is een (herhaalbare) verlenging van de route mogelijk via $c1-d1-d2-c2-d2$, maar dat resulteert uiteraard niet in de kortste route. 

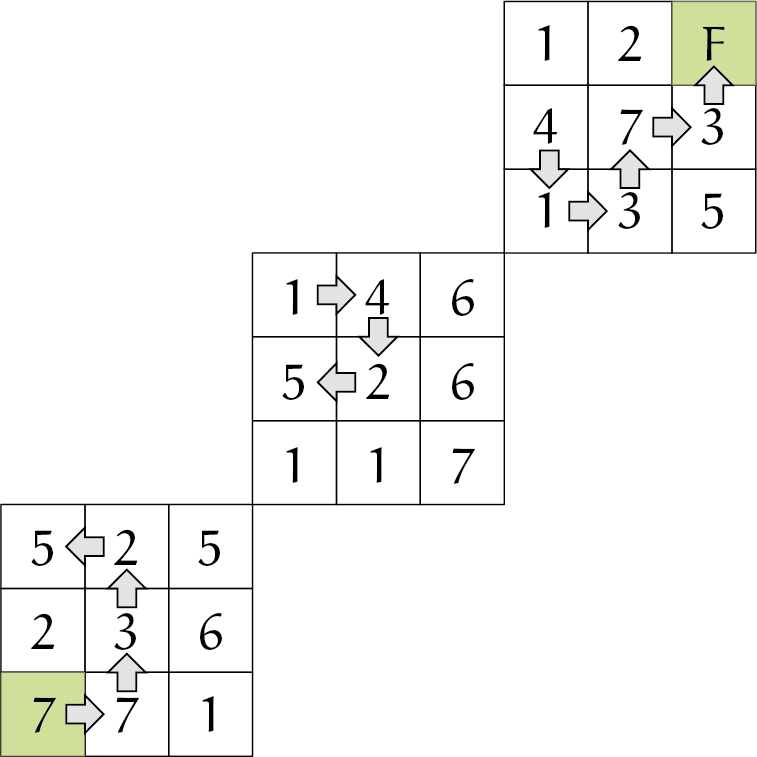
Opgave 5

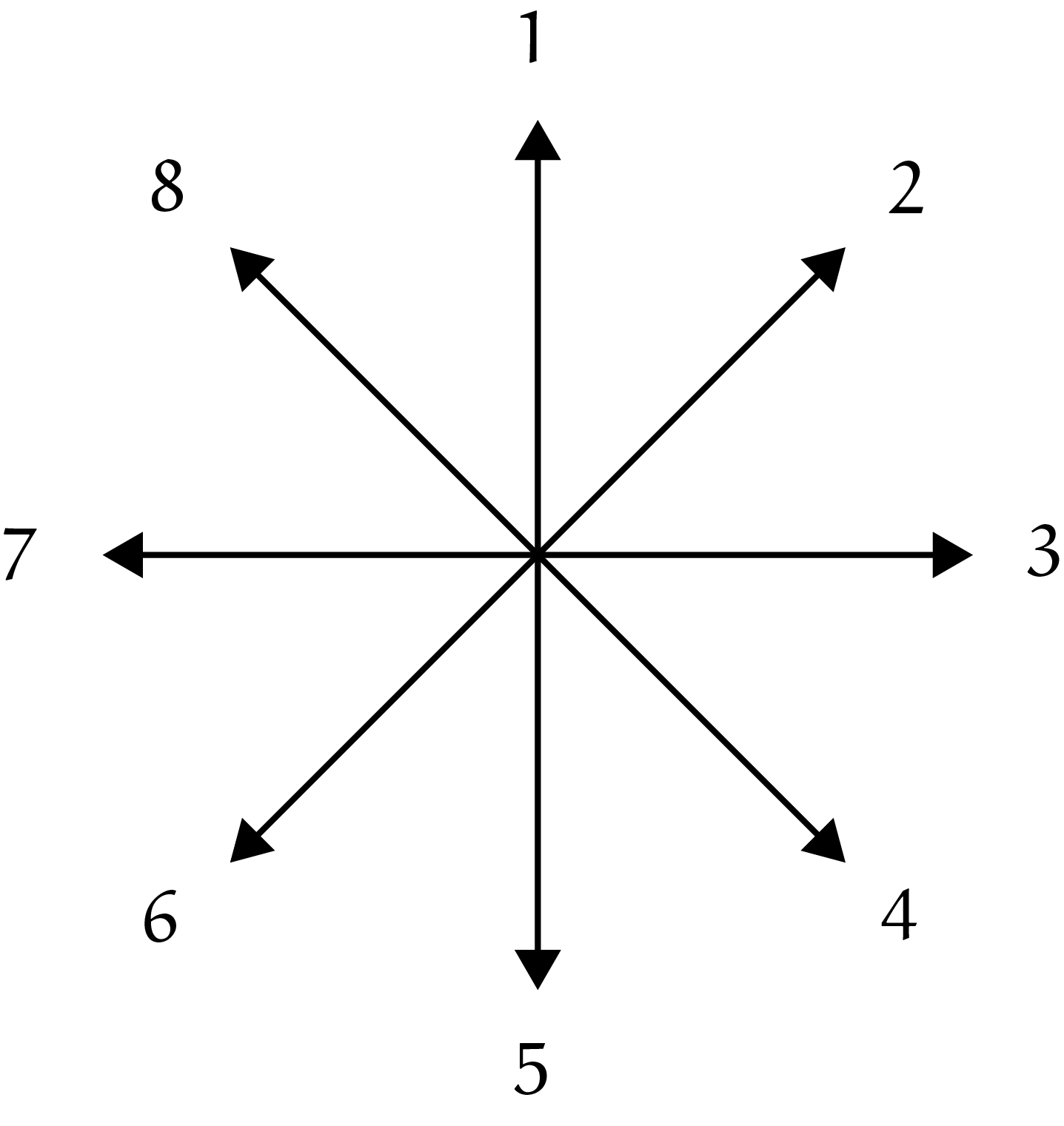
We noteren de 27 blokjes van het 3D-codedoolhof door de drie lagen $O$ (Onder), $M$ (Midden) en $B$ (Boven) vooraf te laten gaan door de waarde. Als er meerdere van die waarden in die laag aanwezig zijn, zetten we er coördinaten bij. Zo is het startblokje $O7_{11}$, omdat de buurman $O7_{21}$ heet.

Er zijn drie mogelijkheden vanuit het starthokje $O7_{11}$.

1. $O2_{12}$. Die ‘$2$’ betekent echter $1$ stap in negatieve $x$-richting, dus de kubus uit. Dat kan niet. Loopt dus dood.
2. $O7_{21}$.Op zich zijn vanuit daar vier voortzettingen mogelijk.
   1. Terug naar $O7_{11}$. Heeft geen zin, want dat zal nooit de kortste route zijn. 
   2. $O_3$. Na $O_3$ volgt (‘$3$’ is 1 stap in positieve $y$-richting): $M2_{23}$. Die ‘$2$’ leidt naar $M5_{13}$. Daarna 1 stap omhoog wordt dus blokje $M1_{13}$. De ‘$1$’ brengt ons naar $M_4$. Die wijst naar $M_2$. Vervolgens moeten we naar $M_5$. Dat betekent 1 stap omhoog (‘$5$’ is dus de trap in dit kubusgebouw), dus komen we aan in $B_4$. Die '$4$' leidt ons naar $B1_{11}$. Daarna volgen $B3_{21}$, $B7$ (vrije keuze); kies $B3_{32}$, die ons naar de finish ‘$F$’ leidt. We hebben dan 14 stappen gemaakt in dit kubusdoolhof.
   3. $O_1$. Loopt dood, want ‘$1$’ betekent 1 stap in positieve $x$-richting en gaat dus de kubus uit.
   4. $M1_{21}$. Leidt naar $M_7$. Dat betekent een vrije keuze van richting. Dat zijn (terug naar $M1_{21}$ heeft geen zin):
      1. $O_1$. Kan niet: verdwijnt daarna uit kubus (zie 2.3).
      2. $M_6$. De ‘$6$’ is code voor 1 stap naar beneden. Dat is $O_6$, maar dat is nog 1 stap naar beneden: kubus uit, dan kan niet. 
      3. $B_5$. Maar ‘$5$’ is 1 stap omhoog: kubus uit.    
3. $M1_{11}$. Een stap in $x+$-richting leidt tot $M1_{21}$, Zie daarna bij 2.4.

De gehele route (zie 2.2) is in onderstaande figuur uitgebeeld.