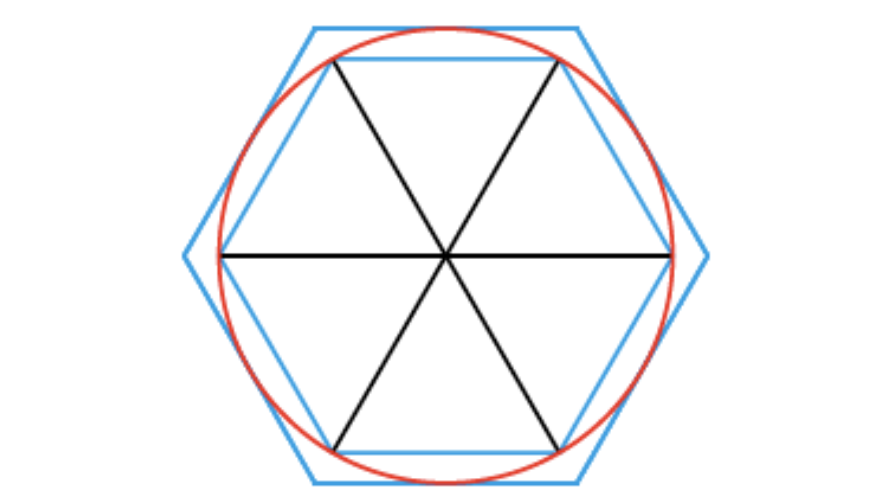
Archimedes (287-212 v. Chr.) slaagde er als eerste in een zeer nauwkeurige breukbenadering van π te vinden: $3 \frac{10}{71} < \pi < 3\frac{1}{7}$. Hij deed dat door, uitgaande van een aan een cirkel in- en omgeschreven regelmatige zeshoek (zie figuur 1), achtereenvolgens de lengte van de zijden van een in- en omgeschreven regelmatige 12-, 24-, 48- en 96-hoek te berekenen. Die berekeningen waren gebaseerd op elementaire stellingen uit de meetkunde en breukbenaderingen van wortels.

Archimedes verdubbelde het aantal zijden dus vier keer. Elke keer hanteerde hij dezelfde methode om de zijde van de volgende veelhoek te berekenen. In dit artikel zie je hoe zijn methode gebruikt kan worden om recursieve formules af te leiden waarmee je de lengte van de zijden van een in- en omgeschreven 2n-hoek kunt berekenen uit die van een in- en omgeschreven n-hoek.

Archimedes onderbouwde zijn methode met twee ‘veronderstellingen’ die hij vermeldt in zijn boek Over de bol en de cilinder:

Veronderstelling 1. Van alle lijnen met dezelfde eindpunten, is de rechte lijn het kortst. (Lijn staat hier voor elke mogelijke verbindingsweg tussen twee punten.)

Het gevolg van deze veronderstelling is dat de omtrek van een ingeschreven veelhoek van een cirkel kleiner is dan de omtrek van die cirkel.

Veronderstelling 2. Als twee lijnen met dezelfde eindpunten concaaf zijn in dezelfde richting en één daarvan ligt geheel tussen de andere en de rechte lijn met dezelfde eindpunten, dan is de ingesloten lijn de kortste van de twee.

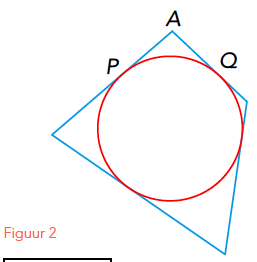
Hieruit volgt dat de omtrek van een omgeschreven veelhoek van een cirkel groter is dan de omtrek van die cirkel, zie figuur 2 (stelling 1 uit Over de bol en de cilinder). Immers, volgens veronderstelling 2 is PA + AQ > boog PQ, enzovoort...

OMGESCHREVEN 2N-HOEK

Van een cirkel met straal 1 is AB een middellijn. CE is een zijde van een omgeschreven regelmatige n-hoek, die de cirkel raakt in A. Archimedes construeert een zijde van de omgeschreven regelmatige 2n-hoek door de bissectrices van de hoeken COA en EOA te trekken (zie figuur 3).

 

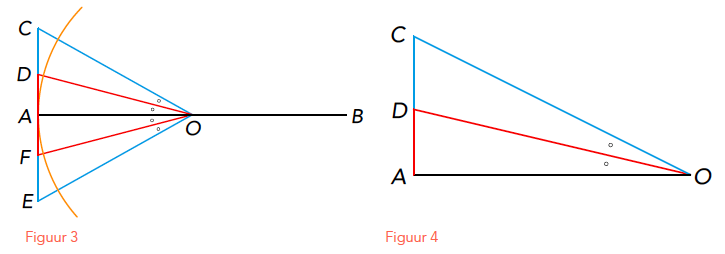
Noteren we met $Z_n$ de lengte van een zijde van de omgeschreven regelmatige n-hoek, dan geldt dus:

$AC = \frac{1}{2} CE = \frac{1}{2} Z_n$ en $AD = \frac{1}{2} FD = \frac{1}{2} Z_{2n}.$

Om $Z_{2n}$ uit te drukken in $Z_n$ gebruikt Archimedes de bissectricestelling, die als stelling 3 in boek VI van de Elementen van Euclides staat.

Bissectricestelling. In een driehoek verdeelt een bissectrice van een hoek de overstaande zijde in stukken die zich verhouden als de aanliggende zijden.

Het bewijs van deze stelling staat in het kader.

BEWIJS VAN DE BISSECTRICESTELLING

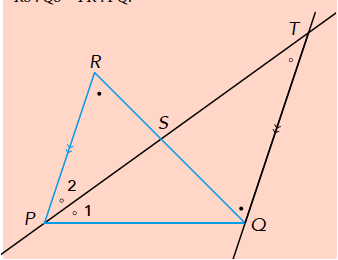
De lijn door Q evenwijdig met PR snijdt de bissectrice van ∠P in T. De driehoeken PRS en TQS zijn gelijkvormig (hh), dus RS : QS = PR : TQ. Er geldt: ∠T = ∠P1 = ∠P2, dus TQ = PQ en RS : QS = PR : PQ.

In driehoek OAC (zie figuur 4) geldt dus:

$$\frac{CD}{AD} =\frac{OC}{OA} .$$

Maar dan geldt natuurlijk ook

$$\frac{CD}{AD}+1=\frac{OC}{OA}+1,$$

ofwel

$$\frac{CD + AD}{AD}=\frac{OC +OA}{OA} .$$

Dus

$$\frac{AC}{AD}=\frac{OC +OA}{OA} ,$$

ofwel

$$\frac{\frac{1}{2} Z_n}{\frac{1}{2} Z_{2n}}= \frac{OC + 1}{1}.$$

Het omkeren van de breuken en vereenvoudigen geeft:

$$Z_{2n} = \frac{1}{OC + 1} Z_n .$$

Met de stelling van Pythagoras vind je OC:

$$OC^2 = OA^2 + AC^2 = 1 + (\frac{1}{2} Z_n)^2 = 1 + \frac{1}{4} Z_n^2.$$

Dus

$$Z_{2n} = \frac{Z_n}{1 + \sqrt{1 + \frac{1}{4} Z_n^2}},$$

of ook

$$Z_{2n} =\frac{2Z_n}{2 + \sqrt{Z_n^2 + 4}}.$$

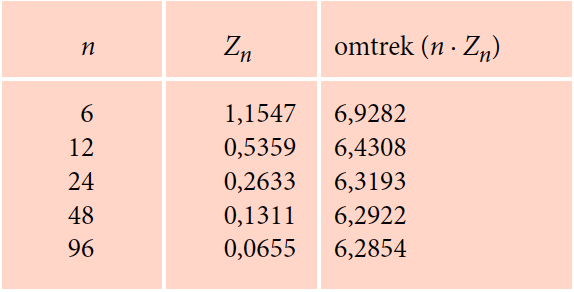
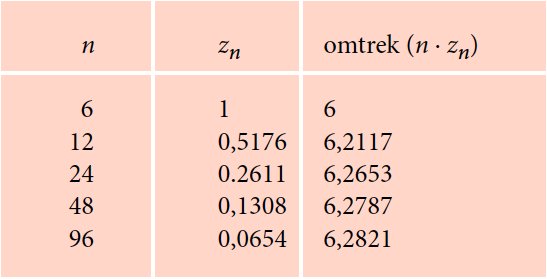
Begin je met een regelmatige omgeschreven zeshoek

(∠AOC = 30°), dan is $Z_6 = 2AC = 2/√3 ≈ 1,1547$. Met een rekenmachine vind je dan de waarden in de volgende tabel:

INGESCHREVEN 2N-HOEK

Een zijde van de ingeschreven regelmatige 2n-hoek uitdrukken in die van de ingeschreven regelmatige n-hoek is wat gecompliceerder. Daarbij heb je de stelling van Thales (ca. 624-545 v. Chr.) nodig:

Stelling van Thales. Ligt een punt C op de cirkel met middellijn AB, dan is ∠ACB een rechte hoek.

Figuur 5 laat het bewijs van deze stelling zien. Je ziet daar de helft van een cirkel met middellijn AB. Punt O is het midden van AB. Lijnstuk OC verdeelt driehoek ABC in twee gelijkbenige driehoeken. Daaruit volgt: ∠C = ∠A + ∠B = 90°.

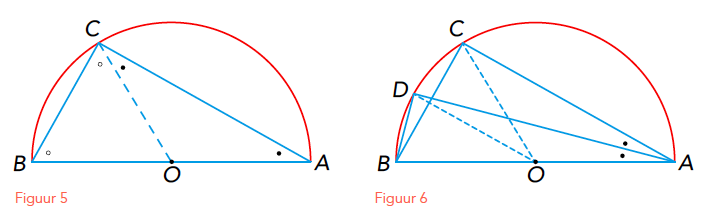
Dezelfde figuur kun je gebruiken om te laten zien dat ∠BOC = 2∠BAC. Noem je ∠OAC = α, dan is ook ∠OCA = α. Verder is ∠AOC = 180° – 2α, dus ∠BOC = 2α.

Nu verder met de berekening van een zijde van de regelmatige ingeschreven 2n-hoek. In de cirkel met straal 1 en middellijn AB is BC een zijde van de ingeschreven regelmatige n-hoek. Archimedes construeert een zijde van de ingeschreven regelmatige 2n-hoek door de bissectrice AD van ∠CAB te trekken (zie figuur 6). Uit het voorgaande is duidelijk dat ∠BOD = 2∠BAD en ∠BOC = 2∠BAC en omdat ∠BAC = 2∠BAD, is dus ook ∠BOC = 2∠BOD.

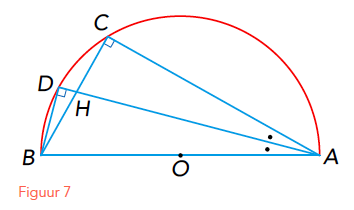
Is $z_n$ de lengte van een zijde van de ingeschreven regelmatige n-hoek, dan geldt dus $BC = z_n$ en $BD = z_{2n}$. Bissectrice AD snijdt lijnstuk BC in H (zie figuur 7). Omdat de hoeken C en D recht zijn (Thales) en de twee hoeken bij A even groot, zijn de driehoeken ADB en ACH gelijkvormig (hh). Er geldt:

$$\frac{AD}{BD}= \frac{AC}{CH} .\ \ \ \ \ \ (1)$$

Volgens de bissectricestelling in driehoek ABC geldt:

$$\frac{AB}{AC}= \frac{BH}{CH}$$

en dan natuurlijk ook

$$\frac{AB}{AC} +1= \frac{BH}{CH} +1$$

waaruit volgt dat

$$\frac{AB+ AC}{AC}= \frac{BH +CH}{CH}= \frac{BC}{CH} .$$

Hieruit volgt dat

$$\frac{AC}{CH}= \frac{AB+ AC}{BC} .$$

Combineer je dit resultaat met (1), dan vind je:

$$\frac{AD}{BD}= \frac{AB+ AC}{BC} .$$

Anders geschreven:

$$\frac{AD}{z_{2n}} = \frac{2+ AC}{z_n} \ \ \ \ \  (2)$$

Om de verhouding met de middellijn AB te vinden, gebruik je de stelling van Pythagoras:

$$\frac{AB^2}{z_{2n}^2} = \frac{AD^2 + z_{2n}^2}{z_{2n}^2} = \frac{AD^2}{z_{2n}^2} +1.\ \ \ \ \ \  (3)$$

Substitutie van (2) in deze vergelijking geeft:

$$\frac{AB^2}{z_{2n}^2} = \frac{(2+ AC)^2}{z_n^2 +1}.$$

Omdat AB = 2 en in driehoek ABC geldt dat $AC = \sqrt{4−z_n^2}$ , vind je

$$\frac{4}{z_{2n}^2} = \frac{(2+ \sqrt{4−z_n^2} )^2 + z_n^2}{z_n^2} = \frac{4+4\sqrt{4−z_n^2} +4−z_n^2 +z_n^2}{z_n^2} = \frac{8+4\sqrt{4−z_n^2}}{z_n^2} ,$$

ofwel

$$z_{2n}^2 = \frac{z_n^2}{2 + \sqrt{4 −z_n^2}}.$$

Begin je met een regelmatige ingeschreven zeshoek, dan is z6 = 1. Met de rekenmachine vind je dan de volgende tabel:

BREUKBENADERINGEN

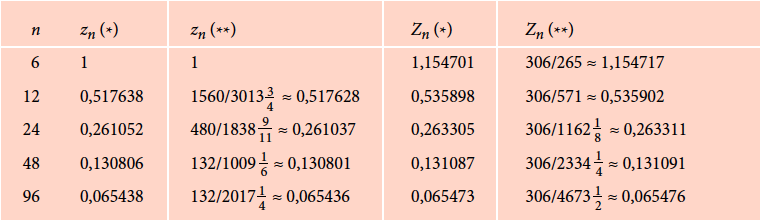
Zoals eerder gezegd, benaderde Archimedes de wortels die hij vond met breuken. In de tabel onderaan de pagina zie je zijn breukbenaderingen (**) naast de waarden uit de tabellen in dit artikel (*). Het geeft eens te meer aan over welke vaardigheden Archimedes beschikte.

Volgens Archimedes geldt voor de verhouding omtrek : middellijn (wat wij nu π noemen):

$$96 \cdot \frac{132}{2017 \frac{1}{4}}: 2 < π <96\cdot \frac{306}{4673\frac{1}{2}}: 2.$$

Dit komt neer op

$$\frac{6336}{2017 \frac{1}{4}}< \pi < \frac{14688}{4673\frac{1}{2}}$$

of ook

$$3+\frac{284\frac{1}{4}}{2017 \frac{1}{4}}< π < 3+\frac{667 \frac{1}{2}}{4673 \frac{1}{2}}.$$

Zoals je kunt controleren, is de eerste breuk groter dan $\frac{10}{71}$ en de tweede kleiner dan $\frac{1}{7}$ .

LITERATUUR

Voor dit artikel is gebruikgemaakt van de vertaling van en het commentaar op de tekst van Archimedes van T.L. Heath in The works of Archimedes (Dover Publications, 2002).