Een liniaal gebruik je doorgaans om lengtes te meten. Heb je twee linialen, dan kun je die gebruiken om getallen op te tellen zónder te rekenen: leg het nulpunt van de ene liniaal bij een getal $r_1$ op de andere liniaal, neem vervolgens een getal $r_2$ op de eerstgenoemde liniaal, en lees ten slotte daartegenover op de andere liniaal de som $r_1 + r_2$ af. Dit lijkt niet de moeite waard om bij stil te staan, maar het is wel een goed opstapje naar de rekenliniaal.

Vermenigvuldigen

Over rekenlinialen heeft al vaker iets in dit blad gestaan – voor het laatst in april van dit jaar (‘Hoe werkt de rekenliniaal’ van Jeanine Daems in Pythagoras 55-5). Een rekenliniaal bestaat uit twee langs elkaar schuivende logaritmische schalen. Dit betekent dat het getal $r > 0$ staat vermeld bij het punt op de schaal dat op afstand ln r (ln staat voor de natuurlijke logaritme) van het referentiepunt van de schaal ligt, en niet zoals bij de gewone liniaal op afstand $r$ van het nulpunt. Bij het referentiepunt staat $r = 1$, omdat ln 1 = 0.
Voeren we dezelfde stappen uit als hierboven en leggen we zodoende een deel van de ene liniaal ter lengte ln $r_1$ en een deel ter lengte ln $r_2$ van de andere aan elkaar, dan tellen hun lengtes gewoon op. De getallen zeggen echter iets anders. Op de logaritmische schaal vinden we bij de lengte ln $r_1$ + ln $r_2$ het getal $r_1r_2$, het product van $r_1$ en $r_2$. Dit volgt uit de rekenregel
$$\ln r_1 + \ln r_2 = \ln r_1r_2.$$
Houd er rekening mee dat voor $0 < r < 1$ geldt dat ln $r$ en ‘lengte’ en ‘afstand’ een minteken hebben. Met een rekenliniaal kunnen we dus vermenigvuldigen, zonder zelf te hoeven rekenen. Op een logaritmische schaal komt het vermenigvuldigen van getallen overeen met het optellen van lengtes, en is in de bovenstaande rekenregel ‘ln’ niet alleen als ‘(natuurlijke) logaritme’ maar ook als ‘lengte’ te lezen!

Complex vermenigvuldigen

Complexe getallen vormen een uitbreiding van gewone, reële getallen. Ze hebben naast een reëel deel ook een imaginair deel: $$z = a + bi.$$ 
Het ‘getal’ $i$ is de imaginaire eenheid, die gekwadrateerd $-1$ oplevert. De reële getallen $a$ en $b$ heten de reële en de imaginaire component van het complexe getal $z$. Een reëel getal kunnen we zien als een complex getal met $b = 0$, terwijl we bij $b \neq 0$ te maken hebben met een ‘echt’ niet-reëel complex getal, en bij $a = 0$ en $b \neq 0$ met een (zuiver) imaginair getal.

Complexe getallen maken het mogelijk om $n$-de-graads vergelijkingen op te lossen. Zo heeft $z^2 = –1$ geen reële oplossing, maar wel twee complexe: $z = ±i.$

Optellen van complexe getallen gebeurt componentsgewijs:
$$z_1 + z_2 = (a + bi) + (c + di) = (a + c) + (b + d)i.$$
Veel interessanter is het vermenigvuldigen, omdat daarbij de bijzondere eigenschap $i^2 = –1$ zich doet gelden:
\begin{align*}z_1z_2 &= (a + bi)(c + di) \\ &= ac + adi + bci + bdi^2 \\ &= (ac – bd) + (ad + bc)i.\end{align*}
Overeenkomstig de rekenliniaal voor de reële vermenigvuldiging, bestaat er ook een hulpmiddel voor de complexe vermenigvuldiging, in de vorm van een cilinder. Voordat we dat instrument gaan beschouwen en bouwen, bestuderen we eerst de complexe getallen en hun vermenigvuldiging wat dieper.

Modulus en argument

Complexe getallen komen voor in paren. Voor het complexe getal $z = a + bi$ definiëren we de complex geconjugeerde, genoteerd als $\bar{z}$ , als $a – bi$. De complex geconjugeerde heeft de mooie eigenschap dat zowel de som $z + \bar{z}$ als het product $z \cdot \bar{z}$ reëel is. Er geldt zelfs dat $z \cdot \bar{z}  = a^2 + b^2$ positief is. De absolute waarde of modulus van het getal $z$, de afstand tot de oorsprong, kan dus geschreven worden als $|z| = \sqrt{(z \cdot \bar{z} )}.$ 
Dit stelt ons in staat de complexe getallen op grootte te groeperen. Alle getallen met een bepaalde $|z| = r > 0$ hebben de gedaante
$$z = r(x + iy)$$

met $x^2 + y^2 = 1$. Het punt $(x, y)$ ligt op de eenheidscirkel en kunnen we schrijven als $x = \cos θ$ en $y = \sin θ$. Het getal

$$z = r(\cos θ + i \sin θ)$$

is dus geheel bepaald door zijn modulus en de hoek $θ$. Er geldt:\begin{align*} a = r \cos θ & \ \ \ \ \ \ \ \mbox{ en} & b = r \sin θ.\end{align*}

De hoek $θ$ heet wel het argument. Omdat de sinus en de cosinus periodiek zijn, zijn er meerdere hoeken die hetzelfde getal $a + bi$ representeren.
De vermenigvuldiging heeft met deze representatie een prachtige eigenschap (we gebruiken de somformules voor sinus en cosinus):
\begin{align*} z_1z_2 &= r_1r_2(\cos θ_1 + i \sin θ_1)(\cos θ_2 + i \sin θ_2) \\
&= r_1r_2[(\cos θ_1 \cos θ_2 – \sin θ_1 \sin θ_2) + (\sin θ_1 \cos θ_2 + \cos θ_1 \sin θ_2)i] \\
&= r_1r_2[\cos (θ_1 + θ_2) + \sin(θ_1 + θ_2)i]. \end{align*}
Je ziet: de modulus van het product is gelijk aan het product van de moduli. En: het argument van het product is de som van de argumenten. Dit inzicht blijkt een verrassende mogelijkheid te bieden.

Vermenigvuldigen met een rekencilinder

Meestal wordt een complex getal voorgesteld als een punt in het platte vlak. De reële en imaginaire componenten zijn de coördinaten van het punt afgezet tegen een rechthoekig assenstelsel, en de modulus en het argument zijn de poolcoördinaten ten opzichte van de oorsprong. In het vlak komt de vermenigvuldiging tot uitdrukking in een draaistrekking.
Het beeld van het complexe vlak is zo stevig gevestigd, dat we haast zouden vergeten dat er nog een andere verschijningsvorm is. Een cilindermantel is eigenlijk een veel natuurlijker oppervlak om de modulus en het argument op uit te zetten (zie figuur bovenaan). Kiezen we bovendien voor de modulus een logaritmische schaal, dan komt de complexe vermenigvuldiging overeen met een verschuiving volgens de rekenliniaal samen met een draaiing om de cilinderas. Zoals een rekenliniaal bestaat uit twee linialen, zo heeft een rekencilinder een binnencilinder die precies past in een doorzichtige cilindermantel.
Hoewel zijn werking is gebaseerd op het vermenigvuldigen van de moduli en het optellen van de argumenten, willen we dit vertalen naar de meer gebruikelijke berekening

$$(a + bi)(c + di) = (ac – bd) + (ad + bc)i.$$
De gebruiksaanwijzing is dan als volgt. Neem op de binnencilinder het getal $a + bi$ in ogenschouw. Schuif en draai daarna de cilinders zo ten opzichte van elkaar dat dit punt wordt overdekt door het referentiepunt $z = 1$ van de doorzichtige buitencilinder. Het getal $c + di$ op de buitencilinder overdekt de gezochte uitkomst, die op de binnencilinder kan worden afgelezen. In figuur 2 hebben we $1 + i$ en $1 – 2i$ weergegeven. Als je deze vectoren vanuit 1 tekent, dan is de som van deze vectoren $3 – i$ (niet getekend).

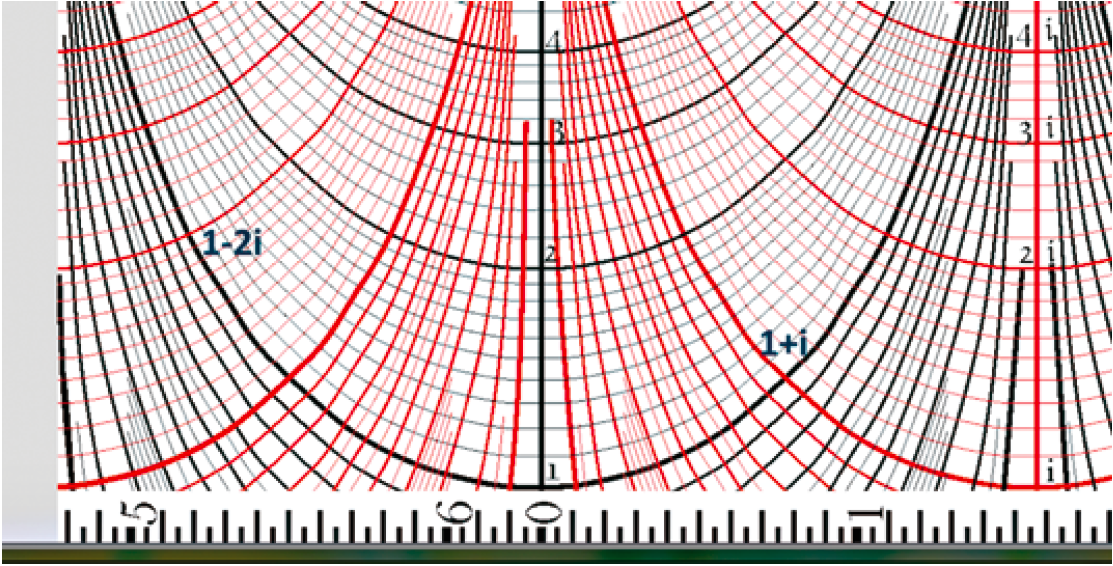
Figuur 2

Waarom werkt de cilinder?

Alle getallen $a + bi$ hebben een $r$ en een $θ$ die samenhangen volgens$$ r = \frac{a}{\cosθ}.$$ Deze betrekking definieert op de cilinder een kromme met $a$ vast en $b$ variabel. Vanwege de logaritmische schaal tekenen we deze kromme als de grafiek van de afstand ln $r$ als functie van $θ$:

$$f(\theta)=\ln \left(\frac{a}{\cos\theta} \right)=\ln\left|a\right| - \ln\left|\cos\theta\right|,$$

met dien verstande dat de definitie van $f$ beperkt is tot de $θ$ waarvoor $\cos θ$ hetzelfde teken heeft als de gegeven $a$.

Evenzo is de kromme met $b$ vast en $a$ variabel:

$$ g(\theta)=\ln \left(\frac{b}{\sin \theta}\right) = \ln\left|b\right| - \ln\left|\sin\theta\right|,$$

daar waar $\sin θ$ hetzelfde teken heeft als $b$. De lijnen $θ = 0, θ = π/2, θ = π$ en $θ = 3π/2$ stellen om beurten de reële en de imaginaire getallen voor.

Eigen onderzoek

Onderzoek nu zelf deze functies en teken hun grafieken voor verschillende waarden van $a$ en $b$, zowel op een vel papier als op een doorzichtig vel. Maak gebruik van verschillende kleuren om het aflezen te vergemakkelijken. Of gebruik figuur 3, te downloaden via http://cs.stmarys.ca/~dawson/sliderule.gif – plak een print van deze fraaie plaat op een kartonnen koker. Rol het doorzichtige vel eromheen en verbind de randen met plakband. Stem de afmetingen van de vellen wel af op de omtrek en de lengte van de koker. Veel plezier met deze alternatieve kijk op de complexe getallen!

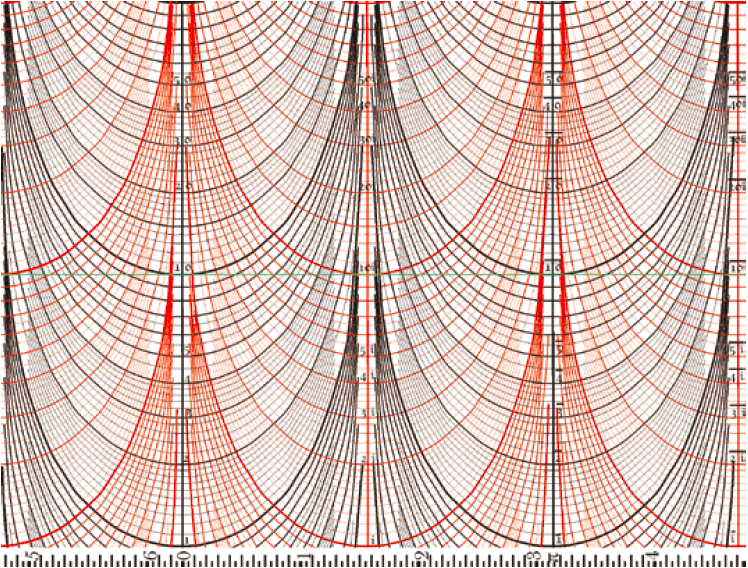
Figuur 3