Het probleem

Uit een lange rij enveloppen, genummerd $1$ tot en met $1\,000\,000$ moeten we die envelop vinden waarin een goudgekleurd stuk papier zit (ook al is de envelop zelf niet van goud, hij dus is wel de gouden envelop).

Nadere informatie: in alle enveloppen met een lager nummer dan de gouden envelop zit een stuk groen papier, die met een hoger nummer bevatten een vel rood papier.

Eerst Een maKkelijke versie

Dit is een bekend zoekprobleem en een veelgebruikte strategie is binair zoeken: ga naar het midden en open envelop $500\,001$ (of $500\,000$). Bij goud ben je klaar, bij rood weet je dat de gouden envelop links van het midden ligt, en bij groen dus rechts van het midden. Je houdt dus de helft van het oorspronkelijke aantal over om te onderzoeken.

Als je dit blijft herhalen ben je in twintig stappen zeker klaar: als je begint met $1\,000\,000$ heb je na twintig keer de helft nemen nog maar één envelop over, en als je altijd maar rood en groen hebt gezien moet dat wel de gouden envelop zijn.

MaAr ...

De puzzel in de krant heeft een extra eis: je mag niet twee keer achter elkaar een envelop met een rood papiertje openen. En: je mag maar $28$ enveloppen openen.

Een valse start

Wat gebeurt er als je weer gaat halveren? Dan gaat het je niet op tijd lukken: als $500\,000$ (of $500\,001$) rood is  moet je, om zeker geen rood papiertje in de volgende envelop te vinden, nummer $1$ nemen ($1$ zou goud kunnen zijn en zelfs $2$ openen leidt dan tot verlies). Dan zijn er na twee stappen $499\,998$ of $499\,999$ enveloppen over; op een haar na de helft dus.

Een grove schatting leert dat in het ergste geval - telkens in het midden een rood papiertje vinden - het aantal overgebleven getallen per twee stappen halveert. Dus na $28$ beurten hebben we dan nog ongeveer $100\,000/2^{14}$ enveloppen over en dat is ongeveer $60$.

Het ideE van Just Bent

We passen de strategie aan. We willen die ene envelop uit de volgende gedwongen zet compenseren: we zorgen dat we, als we een rood papiertje vinden, meer dan de helft terzijde kunnen leggen.

Aan de andere kant, als we te veel richting $1$ gaat en we vinden een groen papiertje dan leggen we minder dan de helft weg en houden we (te veel) meer dan de helft over. We moeten de nieuwe positie met zorg kiezen: niet te veel en niet te weinig richting envelop $1$.

We kiezen een vast getal $p$ in $(0,1)$ en gebruiken dat om telkens een nieuwe envelop te kiezen. Stel we hebben nog $M$ enveloppen over (aan het begin hebben we dus $M=1\,000\,000$); laat ze op volgorde liggen en nummer ze opnieuw met $1$ tot en met $M$ (dat maakt de berekening wat overzichtelijker).

Ga naar positie $(1-p)M$, die kan tussen twee enveloppen liggen, en neem de envelop met nummer $\lceil{(1-p)M}\rceil$  (dit is een veelgebruikte notatie voor "$(1-p)M$ naar boven afgerond").

Zit er een rood vel papier in leg dan enveloppen $\lceil{(1-p)M}\rceil$ tot en met $M$ terzijde en, in de volgende beurt, envelop nummer $1$ (als daar geen gouden papiertje in zit).

Zit er een groen vel papier in nummer $\lceil{(1-p)M}\rceil$ leg dan enveloppen $1$ tot en met $\lceil{(1-p)M}\rceil$ terzijde en ga door met het nieuwe aantal enveloppen.

We vergelijken twee mogelijkheden. De eerste met een rood papiertje en een tweede gedwongen zet. De tweede waarbij twee keer groen wordt gevonden.

Voor we dat doen moeten we eerst wat opmerkingen maken over naar boven en naar beneden afronden. Met $\lfloor{(1-p)M}\rfloor$ geven we "$(1-p)M$ naar beneden afgerond" aan.

Het getal $p$ dat we nemen is irrationaal, dus we hebben altijd de volgende ongelijkheden.  $$
\lfloor{pM}\rfloor<pM<\lceil{pM}\rceil
$$
En daarmee ook
$$
M-\lfloor{pM}\rfloor>(1-p)M>M-\lceil{pM}\rceil
$$ waaruit weer volgt
$$ M-\lfloor{pM}\rfloor = \lceil{(1-p)M}\rceil \text{ en } M-\lceil{pM}\rceil=\lfloor{(1-p)M}\rfloor $$ en andersom ook $$ M-\lceil{(1-p)M}\rceil=\lfloor{pM}\rfloor  \text{ en } M-\lfloor{(1-p)M}\rfloor=\lceil{pM}\rceil $$

Deze dingen hebben we nodig bij het bepalen van de aantallen enveloppen die na beide mogelijkheden overblijven.

Rood-groen

In de eerste stap leggen we enveloppen $\lceil{(1-p)M}\rceil$ tot en met $M$ weg en houden we dus $\lfloor{(1-p)M}\rfloor$ enveloppen over. Na de gedwongen zet van envelop $1$ hebben we dus nog $\lfloor{(1-p)M}\rfloor-1$ enveloppen over.

In het plaatje staat niet-afgerond weergeven wat terzijde is gelegd en wat nog over is.

Groen-groen

Nu leggen we dus eerst $\lceil{(1-p)M}\rceil$ enveloppen terzijde en houden we $M-\lceil{(1-p)M}\rceil=\lfloor{pM}\rfloor$ enveloppen over. Noem dat aantal even $N$, dan hebben we na de tweede stap dus nog $\lfloor{pN}\rfloor$ enveloppen. Dat kunnen we, heel indrukwekkend, opschrijven als $\bigl\lfloor{p\lfloor{pM}\rfloor}\bigr\rfloor$.

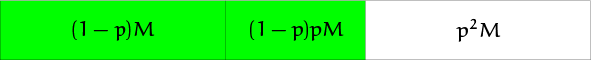
In het plaatje staat niet-afgerond weergeven wat terzijde is gelegd en wat nog over is.

Vergelijken en p bepalen

Als $M$ heel groot is, en zeker als $M=1\,000\,000$, zullen de afgeronde waarden relatief weining van de echte waarden verschillen. Wat we willen is dat het niet veel uitmaakt of we rood-groen of groen-groen tegenkomen. We willen dus dat $(1-p)M$ ongeveer gelijk is aan $p^2M$. Laten we maar zorgen dat $p$ zó is dat $1-p=p^2$; dan kijken we later wel wat de invloed van afronden is.

Welnu $p^2+p-1=0$ lossen we snel op door kwadraat afsplitsen: $p^2+p-1$ is gelijk aan $(p+\frac{1}{2})^2-\frac{5}{4}$ (controleer maar) en dus vinden we

$$
p=-\frac{1}{2}-\frac{1}{2}\sqrt{5}\text{ of }p=-\frac{1}{2}+\frac{1}{2}\sqrt{5}
$$

alleen de laatste is positief, dus die moeten we hebben.

Terzijde: in de column wordt dit in verband gebracht met de gulden snede. Hoezo? Welnu, de gulden snede, $\phi$, is gelijk aan $\frac{1}{2}+\frac{1}{2}\sqrt{5}$ en je reken zo na dat $p\phi=1$, dus $p=1/\phi$.

Vanaf nu is onze $p$ dus gelijk aan $-\frac{1}{2}+\frac{1}{2}\sqrt{5}$. We blijven gewoon $p$ schrijven en we gaan ook gebruiken dat $p^2=1-p$. Voor straks geven we ook nog wat decimalen van $p$ en $1-p$: $$
p=-\frac{1}{2}+\frac{1}{2}\sqrt{5}\approx 0{,}61803398874989484820.
$$

en

$$
1-p=\frac{3}{2}-\frac{1}{2}\sqrt{5}\approx0{,}38196601125010515180.
$$ 

Nauwkeurige Analyse

We gaan nu heel naukeurig kijken hoeveel verschil er is tussen rood-groen en groen-groen; dat moet om het aantal benodigde zetten te kunnen bepalen.

Het begin

Laten we kijken wat beide wegen aan het begin opleveren (en bekijken alleen gevallen waarin we geen goud vinden).

We nemen envelop nummer $381\,967$. Bij rood-groen houden we dus $381\,966-1=381\,965$ enveloppen over.

Bij groen-groen hebben we na de eerste zet nog $1\,000\,000-381\,967=618\,033$ over en bij de tweede zet nog $381\,965$.

Dat begint dus goed.

En verder  

Neem weer een willekeurige $M$. Is er een relatie tussen $\lfloor{(1-p)M}\rfloor-1$ en $\left\lfloor{p\lfloor{pM}\rfloor}\right\rfloor$? Ja die is er want we hebben $1-p=p^2$; we gaan dus $\lfloor{p^2M}\rfloor-1$ en $\left\lfloor{p\lfloor{pM}\rfloor}\right\rfloor$ vergelijken.

Om te beginnen
$$
0<pM-\lfloor{pM}\rfloor<1
$$
en dus 
$$
0<p^2M-p\lfloor{pM}\rfloor<p<1
$$
Dat impliceert dat ten hoogste één natuurlijk getal tussen $p\lfloor{pM}\rfloor$ en $p^2M$ kan zitten en dat 
$$
p\lfloor{pM}\rfloor>\lfloor{p^2M}\rfloor-1 
$$
En hieruit volgt dan
$$
\bigl\lfloor{p\lfloor{pM}\rfloor}\ge \lfloor{(1-p)M}\rfloor-1
$$
We zien dus dat groen-groen potentieel ongunstiger is dan rood-groen.

Het verloOp van de aAntallen envelopPen

Als we de extreme situatie bekijken waarin we alleen maar groene papiertjes vinden krijgen we een rij getallen $M_0$, $M_1$, $M_2, \dots$, waarin $M_0=1\,000\,000$ en telkens $M_{k+1}=\lfloor{p*M_k}\rfloor$. Voor die rij geldt dat $M_{27}=1$ en op dat moment hebben we dan meteen de gouden envelop te pakken.

Dat wil zeggen, een wiskundige is klaar: we hebben $27$ enveloppen geopend en de ene die nog over is, de $28$ste, moet dan wel de gouden envelop zijn.

De regels zeggen echter dat we het gouden papiertje echt moeten waarnemen. We moeten die $28$ste envelop dus nog oppakken en openen, maar dan hebben we aan de eis voldaan dat we het gouden papiertje uiterlijk uit de $28$ste envelop moeten halen.

Bekijk nu een andere rij mogelijkheden: $N_0$, $N_1$, $N_2, \dots$. Tot het eerste moment, zeg moment $k$, dat je een rood papiertje vindt geldt dat $M_i=N_i$. Dan geldt 

$$
N_k=\lfloor{(1-p)N_{k-1}\rfloor}
   =\lfloor{(1-p)M_{k-1}\rfloor}\le\lfloor{pM_{k-1}\rfloor}=M_k.
$$

Omdat het verschil tussen $1-p$ en $p$ vrij groot is zal bij kleine $k$ al gauw $N_k<M_k$ gelden. Dat hebben we bij Het begin gezien: als $k=1$ dan $M_1=618\,033$ en $N_1=381\,966$.

Maar na de volgende stap hebben we $N_{k+1}=N_k-1$ en bij $k=1$ zagen we dat weer $N_{k+1}=M_{k+1}$; maar we weten dat in ieder geval zeker $N_{k+1}\le M_{k+1}$ geldt. Bij elke volgend rood papiertje herhaalt dit verschijnsel zich en we zien dus dat altijd $N_k\le M_k$.

Met andere woorden: waar de gouden envelop ook ligt: als je deze strategie volgt heb je na uiterlijk $27$ stappen de gouden envelop zeker gelokaliseerd en in de volgende stap geopend; of eerder natuurlijk als je mazzel hebt.

Opmerking

Er zijn vrij veel getallen $M$ waarvoor $\left\lfloor{p\lfloor{pM}\rfloor}\right\rfloor> \lfloor{(1-p)M}\rfloor-1$ geldt (laat de computer maar zoeken). Dat betekent dat de kans groot is dat je rij getallen op den duur echt kleiner zal zijn dan de groene rij. Dus ook zonder mazzel hoef je vaak minder dan $28$ enveloppen te openen.

Nog een opmerking

Je moet echt naar boven afronden. Als je consequent naar beneden zou afronden dan zou de groene rij voldoen aan $M_{k+1}=\lceil{p*M_k}\rceil$. Maar als je dat doorrekent zie je dat je dan pas bij stap 29 de gouden envelop te pakken hebt.