Opgave 1 (Nederlandse Wiskunde Olympiade, finale 2016)

a. Op een lange stoep staat een rij van 999 getallen geschreven met stoepkrijt. De getallen hoeven niet op volgorde van klein naar groot te staan en ze hoeven niet allemaal verschillend te zijn. Merlijn omcirkelt 500 van de getallen met rood krijt. De rood omcirkelde getallen blijken van links naar rechts precies de getallen 1, 2, 3, ..., 499, 500 te zijn. Vervolgens omcirkelt Jeroen 500 van de getallen met blauw krijt. De blauw omcirkelde getallen blijken van links naar rechts precies de getallen 500, 499, 498, ... , 2, 1 te zijn. Bewijs dat het middelste getal in de rij van 999 getallen zowel rood als blauw omcirkeld is.

b. Merlijn en Jeroen steken de straat over en daar staat ook een rij van 999 getallen op de stoep geschreven. Weer omcirkelt Merlijn 500 van de getallen met rood krijt. Opnieuw blijken de rood omcirkelde getallen van links naar rechts precies de getallen 1, 2, 3, ..., 499, 500 te zijn. Nu omcirkelt Jeroen ook 500 van de getallen, niet per se dezelfde als Merlijn, met groen krijt. De groen omcirkelde getallen blijken van links naar rechts ook de getallen 1, 2, 3, ..., 499, 500 te zijn.

Bewijs: er is een getal dat zowel rood als groen omcirkeld is en dat niet het middelste getal in de rij van 999 getallen is.

 Vraag a

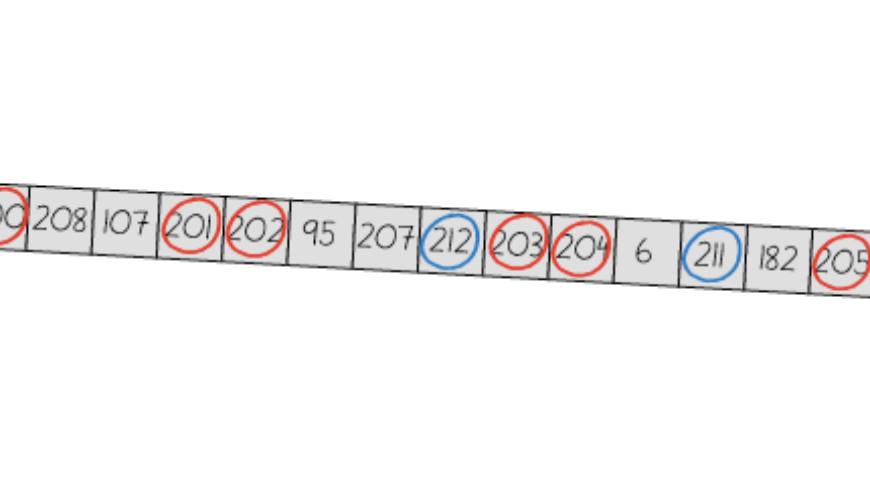
Een lange stoep met 999 getallen... Hoe zou je aan een opgave met zo’n context kunnen beginnen? De lengte van de stoep maakt het lastig om een voorbeeld te bekijken. Maar gelukkig kunnen we, zoals zo vaak bij olympiade-opgaven, de opgave eerst ‘iets kleiner maken’. Het valt op dat het getal 999 ongeveer tweemaal zo groot is als het getal 500: er geldt 999 = 500 · 2 – 1.

Laten we nu het getal 500 eens vervangen door een kleiner getal, zoals 3. Dan krijgen we de volgende kleinere situatie. Op de stoep staan 3 · 2 – 1 = 5 getallen. Merlijn omcirkelt 3 van deze getallen met rood krijt, en deze blijken van links naar rechts precies 1, 2, 3 te zijn. Jeroen omcirkelt 3 van deze getallen met blauw krijt, en deze blijken van links naar rechts precies 3, 2, 1 te zijn.

Van deze kleinere versie van de opgave kunnen we wel enkele voorbeeldjes bekijken. Je ziet er een aantal op de volgende pagina. In al deze voorbeelden is het middelste getal inderdaad dubbel omcirkeld. Er geldt zelfs steeds dat er geen enkel ander getal dubbel omcirkeld is. Zouden we dit kunnen bewijzen? Als dat lukt, en het ook voor de oorspronkelijke opgave met 999 getallen lukt, hebben we daar misschien iets aan bij het oplossen van de opgave. Daarvoor moeten we twee dingen laten zien: ten eerste dat er altijd minstens één getal dubbel omcirkeld is en ten tweede dat er hooguit één getal dubbel omcirkeld is.

Laten we met het eerste beginnen. We zien in alle voorbeelden dat er precies zes cirkels getekend zijn. Dat moet ook wel, want Merlijn en Jeroen tekenen elk precies drie cirkels. Er zijn echter maar vijf getallen. Er moet dus inderdaad wel een getal zijn dat dubbel omcirkeld is! We controleren meteen of zo’n redenering ook in de opgave zelf, met 999 getallen, werkt. En dat blijkt het geval te zijn. Merlijn en Jeroen omcirkelen samen precies 500 · 2 = 1000 getallen. Er zijn echter maar 999 getallen om te omcirkelen, dus moet er een getal dubbel omcirkeld zijn.

Kunnen we ook laten zien dat er maar hooguit één van de 999 getallen dubbel omcirkeld is? Laten we eens kijken wat er gebeurt als dit juist niet waar is. Dan zijn er dus minstens twee getallen dubbel omcirkeld. Laten we deze getallen even a en b noemen, waarbij a links van b staat. Dat zou er als volgt uit zien:

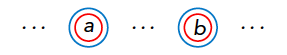
We zien dat a en b beide voorkomen in Merlijns rijtje 1, 2, ..., 500, want a en b zijn beide rood omcirkeld. Maar dan moet a kleiner zijn dan b, want de getallen in Merlijns rijtje staan in oplopende volgorde. Ook geldt dat a en b beide in Jeroens rijtje voorkomen. Maar Jeroens rijtje staat juist in aflopende volgorde, dus moet nu ook gelden dat a groter is dan b. Dat kan natuurlijk niet! De aanname dat er minstens twee getallen dubbel omcirkeld zijn, kan dus niet juist zijn. We kunnen dus concluderen dat er inderdaad maar hooguit één getal omcirkeld is. Omdat we al wisten dat er minstens één getal dubbel omcirkeld is, hebben we hiermee laten zien dat er precies één van de 999 getallen dubbel omcirkeld is. We willen nu graag bewijzen dat dit dubbel omcirkelde getal wel het middelste getal moet zijn.

Er zijn nog meer leuke dingen te zien in onze voorbeeldjes. Er geldt bijvoorbeeld steeds dat er géén getallen zijn die helemaal niet omcirkeld zijn. Kunnen we dit ook voor de opgave met 999 getallen bewijzen? Stel eens dat er wél een getal is dat niet omcirkeld is. Dan tekenen Merlijn en Jeroen samen nog steeds 1000 cirkels, maar ze gebruiken hiervoor hooguit 998 van de getallen. Omdat een getal niet vaker dan twee keer omcirkeld kan worden, moeten er dan dus wel minstens twee getallen zijn die dubbel omcirkeld zijn. Maar we hebben net al gezien dat dat niet kan! We kunnen dus concluderen dat er geen getallen zijn die niet omcirkeld zijn.

We zijn al een heel eind op weg. Voor het laatste stapje kunnen we opnieuw naar onze voorbeeldjes kijken. Laten we de getallen links van het dubbel omcirkelde getal bekijken. De getallen kleiner dan het dubbel omcirkelde getal komen hier allemaal precies één keer voor, en zijn rood omcirkeld. De getallen groter dan het dubbel omcirkelde getal komen hier ook allemaal precies één keer voor, en zijn juist blauw omcirkeld. Laten we proberen dit in het algemeen te bewijzen.

We noemen het enige dubbel omcirkelde getal even c, en we bekijken de getallen links van het dubbel omcirkelde getal. Deze getallen zijn dan allemaal precies één keer omcirkeld. We kunnen deze getallen dus opdelen in rood omcirkelde getallen en blauw omcirkelde getallen. De rood omcirkelde getallen zijn onderdeel van Merlijns rij $$1, 2, ..., c – 1, c, c + 1, ..., 499, 500.$$

Omdat de dubbel omcirkelde c in de rode rij van Merlijn staat, moeten de rood omcirkelde getallen links van hiervan precies 1, 2, ..., c – 1 zijn. Dit zijn samen dus c – 1 rode getallen. De blauw omcirkelde getallen zijn juist onderdeel van Jeroens rij $$500, 499, ..., c + 1, c, c – 1, ..., 2, 1.$$ De dubbel omcirkelde c staat ook in Jeroens blauwe rij, dus de blauwe getallen links van het dubbel omcirkelde getal zijn precies 500, 499, ..., c + 1. Dit zijn samen precies 500 – c getallen. Er staan links van het dubbel omcirkelde getal dus in totaal precies (c – 1) + (500 – c) = 499 getallen. Het dubbel omcirkelde getal is dus het 500ste getal dat op de stoep staat, en staat dus precies in het midden! Hiermee is vraag a opgelost.

Vraag b

Net als bij vraag a kunnen we bewijzen dat er minstens één getal dubbel omcirkeld is. Echter, ons argument dat er ook hooguit één getal dubbel omcirkeld is, werkt nu niet meer, omdat de rijen die Merlijn en Jeroen omcirkelen allebei in oplopende volgorde staan. Wie weet hebben ze wel precies dezelfde 500 getallen omcirkeld.

Gelukkig kunnen we dit omzeilen. Als er minstens twee getallen dubbel omcirkeld zijn, dan is één van deze twee zeker niet het middelste getal. Dus in dat geval is de opgave al opgelost! Laten we dus het geval bekijken waarin er precies één getal dubbel omcirkeld is. Dan kunnen we weer net als bij vraag a bewijzen dat er geen getal is dat helemaal niet omcirkeld is.

Noem het enige dubbel omcirkelde getal opnieuw c. We bekijken opnieuw de getallen die links van het dubbel omcirkelde getal staan en delen deze nu juist op in rood omcirkelde getallen en in groen omcirkelde getallen. Er volgt net als in vraag a dat de rood omcirkelde getallen precies 1, 2, ..., c – 1 zijn. Maar omdat Jeroen nu ook de rij 1, 2, ..., 500 heeft omcirkeld, geldt nu ook dat de groen omcirkelde getallen precies 1, 2, ..., c – 1 zijn. Omdat er geen getallen zijn die helemaal niet omcirkeld zijn, staan er links van het dubbel omcirkelde getal dus precies 2(c – 1) getallen.

Met deze informatie kunnen we het bewijs afmaken. Links van het middelste getal van de rij staan precies 499 getallen, en links van het dubbel omcirkelde getal staan dus 2(c – 1) getallen. Maar 499 is oneven en 2(c – 1) is even, dus deze twee getallen kunnen niet gelijk aan elkaar zijn. We concluderen dat het dubbel omcirkelde getal niet het middelste getal van de rij kan zijn, zoals we wilden.

Terugblik

Op het eerste gezicht leek deze opgave misschien nogal intimiderend, omdat er zo veel getallen op de stoep staan. Maar door een ‘kleinere versie’ van de opgave te bekijken, konden we toch een gevoel krijgen voor wat er aan de hand is. De observaties over de voorbeelden voor een stoep met 5 getallen, bleken ook van toepassing te zijn op de ‘grote’ stoep met 999 getallen, en hebben ons geholpen de opgave op te lossen. Deze strategie komt vaker van pas. Bij opgave 2 van de finale was het bijvoorbeeld ook handig om eerst wat kleine versies te bekijken. Wil je weten hoe dat werkt? Ga dan naar http://www.wiskundeolympiade.nl/video.html .