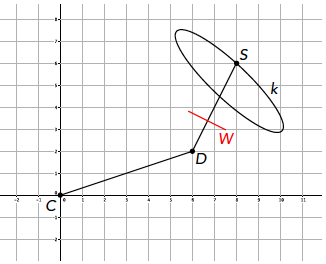
De bekendste planimeter is de zogeheten poolplanimeter. Een foto van dit instrument zie je in figuur 1. Een schematische poolplanimeter is in figuur 2 getekend.

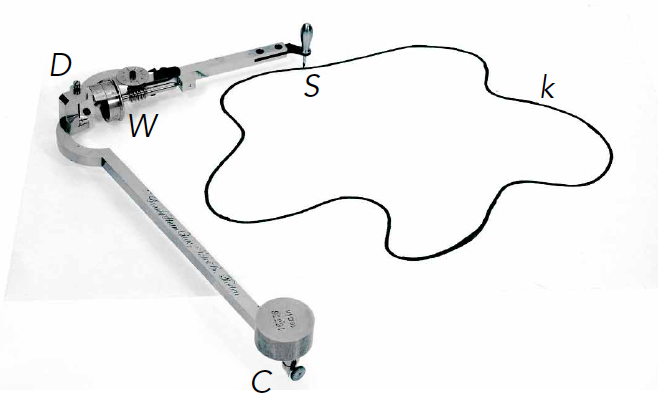
De pool C van de planimeter wordt vastgezet, met een pin of gewicht, op een willekeurige plek op het papier waarop de kromme staat. In figuur 2 ligt C in de oorsprong van het getekende coördinatenstelsel. Om C kan een stang met vaste lengte CD draaien. Op de foto in figuur 1 is punt D het einde van het kleine boogje. Vervolgens kan er weer een stang met constante lengte DS om D draaien. Onder aan S zit een puntje, dat rust op het papier of de kaart. Dwars op de stang DS zit een wieltje W, dat kan draaien (en slippen) als het over het papier loopt. De planimeter geeft het aantal omwentelingen van W weer, maar hoe dat technisch precies zit, is voor dit verhaal niet relevant. 

Gebruik en werking

Het is de bedoeling om met S een willekeurige gesloten kromme, in de tekening k, in een enkele gehele omloop te volgen.Tijdens het volgen van de kromme k beweegt het wieltje W over het vlak. In de tekening zit het wieltje ergens (de plaats is niet van belang) dwars op de stang DS. Tijdens de rondgang met het punt S over de kromme k zal het wieltje draaien; soms langzaam, soms snel, soms heen, soms terug, maar uiteindelijk, na een volledige kromme k, zal het wieltje W een aantal omwentelingen hebben afgelegd.

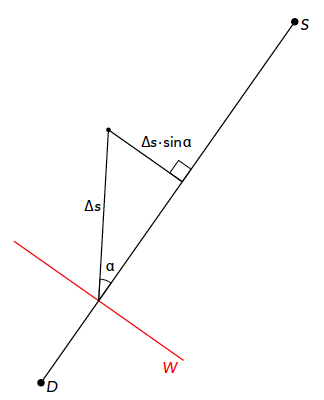
Een belangrijk punt is nog het volgende. Als tijdens het volgen van een stukje van de kromme k punt D even niet van zijn plaats komt, volgt het wieltje W een stukje Δs van een cirkel met straal DW. Het metertje geeft dan een extra aantal omwentelingen aan van Δs/O, met O de omtrek van het wieltje. Het wieltje draait dan en schuift niet. Maar het kan ook zijn dat de stang DS een stukje geheel volgens zijn eigen richting beweegt. Dan draait W in het geheel niet, maar verschuift alleen maar. De stand van het metertje op W verandert daarbij niet. Tussen deze twee uitersten zal het bij de rondloop natuurlijk meestal zo zijn dat W deels schuift en deels draait. Als het middelpunt van W over een klein stukje Δs beweegt in een richting die een hoek α maakt met DS, dan geeft het metertje bij W een draaiing aan van (Δs/O) · sin(α) (zie figuur 3). We zullen hiervan bij onze verdere berekeningen steeds gebruik maken. Overigens vergt het natuurlijk nog wel wat natuurkundig denkwerk om echt aan te tonen dat deze uitdrukking met de sinus juist is. Wiskundig gezien lijkt het gemakkelijk. Het natuurkundige aspect met de wrijvingskrachten slaan we hier over.

IJken van de planimeter

Laten we nu de stand w van het wieltje W opschrijven als we S op een punt van k neergezet hebben. Vervolgens volvoeren we een volledige weg langs k. Laten we aannemen dat w toeneemt, als we rondgaan tegen de klok in. Aan het eind meten we weer de stand van w. Het verschil Δw is nu recht evenredig met de oppervlakte omsloten door k. Het precieze bewijs zien we straks. Maar nu eerst: met welke factor f moeten we Δw vermenigvuldigen om de oppervlakte A in bijvoorbeeld cm$^2$ te krijgen? Kortom, hoe ijken we de planimeter?

Dat is niet moeilijk. Teken op een vel papier een vierkant van precies 10 cm bij 10 cm. De oppervlakte is dan 100 $cm^2$. Ga met S de vier zijden van het vierkant af en lees Δw' af. Dan moeten we nemen: f = 100/Δw'. De oppervlakte A omsloten door k is dan gelijk aan f · Δw. Na ijking kun je natuurlijk op het wiel in plaats van het aantal omwentelingen ook het aantal cm2 zetten, zodat je na een volledige rondgang over de kromme k meteen de oppervlakte kunt aflezen.

Een bijzondere kromme

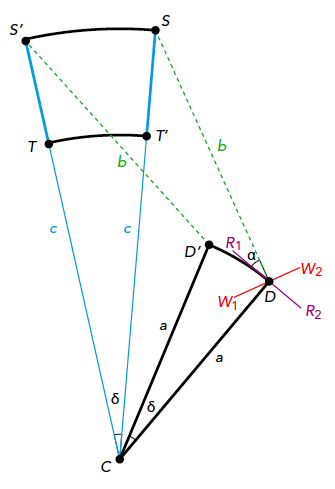
We gaan eerst de oppervlakte bepalen van een bijzondere kromme: SS'TT'. Deze zal ons in het vervolg goed van pas komen. Kijk daarvoor naar figuur 4. Het centrum C van de planimeter, het draaipunt D en het volgpunt S zijn dezelfde als in de beschrijving van de planimeter. We beschrijven met S eerst een cirkelboog SS' met een vaste straal c. Dat houdt in dat de hoek bij D (∠SDC) tijdens het volgen van boog SS' constant blijft. De loodlijn op het wiel $W_1W_2$ maakt met de beweging van D langs de cirkelboog DD' dan steeds dezelfde hoek α. Het wiel draait, gaande van D naar D', dus over een afstand $w_1$:

$$w_1 = boog(DD' ) · sin(α_1)$$

Stel, voor het gemak, dat O = 1. We hebben α een index 1 gegeven, omdat we dadelijk bij het passeren van boog(TT' ) een andere α krijgen. De lijnstukken CS en CD draaien beide over een hoek δ. Dan geldt: boog(DD' ) = aδ, waarbij a = CD. (Als hoekeenheid nemen we de radiaal; 2π rad = 360°.) Dus: $$w_1 = aδ · sin(α_1).$$ Nu kijken we naar de oppervlakte $A_1$ van ‘driehoek’ CSS' en de oppervlakte $A_1$* van ‘driehoek’ CDD'. De hoogteverhouding is c/a en bij gelijke tophoeken δ geldt voor de verhouding van de oppervlaktes: $$\frac{A_1}{A_1*} = \frac{c^2}{a^2}.$$ Daarmee krijgen we: $$A_1 = \frac{c_1^2}{a^2} ·A_1* = \frac{c_1^2}{a^2} · \frac{1}{2} DD'·a$$ $$ = \frac{c_1^2}{a^2} · \frac{1}{2} a^2 · δ = \frac{1}{2} c_1^2 δ.$$ We hebben c ook voorzien van een index 1, omdat we bij de passage van T naar T' een c2 gaan gebruiken. We hebben de gewone formule voor de oppervlakte van een driehoek gebruikt: ‘oppervlakte = half × basis × hoogte’. (Dat klopt ook met een cirkelboog, omdat je in gedachten de driehoek in heel veel kleine driehoekjes kunt verdelen met zeer kleine basis en steeds hoogte a.) Vervolgens zoeken we het verband tussen $A_1$ en $w_1$ door $c_1^2$ te berekenen met behulp van de cosinusregel in ΔCDS: $$c_1^2 = a^2 + b^2 – 2ab · cos(\frac{1}{2} π + α_1)$$ $$= a^2 + b^2 + 2ab · sin(α_1).$$ Als we dit invullen in de formule voor $A_1$ en gebruikmaken van de formule voor $w_1$, krijgen we $$A_1 = \frac{1}{2} δ(a^2 + b^2 + 2ab · sin(α_1))$$ $$= b · w_1 + \frac{1}{2} δ(a^2 + b^2).$$ Voor we verder gaan naar de passage over boog(TT' ), kijken we naar de passages S'T en T'S.

Tijdens de eerste passage gaat ΔCD'S' over in een driehoek met basis $CT = c_2$. Tijdens die passage draait het wiel over w*. We gaan die waarde niet berekenen, omdat bij de passage van T' naar S de basis van de driehoek weer toeneemt naar de oorspronkelijke c en de gehele driehoek weer naar de oorspronkelijke driehoek. Daarbij draait het wiel natuurlijk weer over w*, maar dan in tegengestelde richting. Beide draaiingen samen geven dus een draaiing 0.

Bij de passage van T naar T' is er dus een vaste andere driehoek met basis $c_2$ die roteert over δ. De waarden van a en b blijven natuurlijk gelijk. Met dezelfde berekening als die voor $A_1$ krijgen we nu de volgende uitdrukking voor de oppervlakte $A_2$ van ‘driehoek’ CTT': $$A_2 = \frac{1}{2} δ(a^2 + b^2 + 2ab · sin(α_2))$$ $$= b · w_2 + \frac{1}{2} δ(a^2 + b^2).$$ We moeten wel beseffen dat we hier alle waarden positief genomen hebben. Maar doordat het wiel bij de laatste passage de andere kant opdraait, wordt $w_2$ in mindering gebracht op $w_1$. De afgelezen waarde w na een volledige passage over SS'TT' is dus $w = w_1 – w_2$. Het verschil A van $A_1$ en $A_2$, de omsloten oppervlakte van de curve k = SS'TT', levert dan $$A = A_1 – A_2 = b(w_2 – w_1) = b · w.$$

We zien nu dat de omsloten oppervlakte gelijk is aan het product van de constante b, die bekend is, en de afgelezen waarde van het wiel w. Door een juiste ijking kunnen we de getalletjes op het wiel precies gelijk maken aan de omsloten oppervlakte.

Oppervlakte van een willekeurige kromme

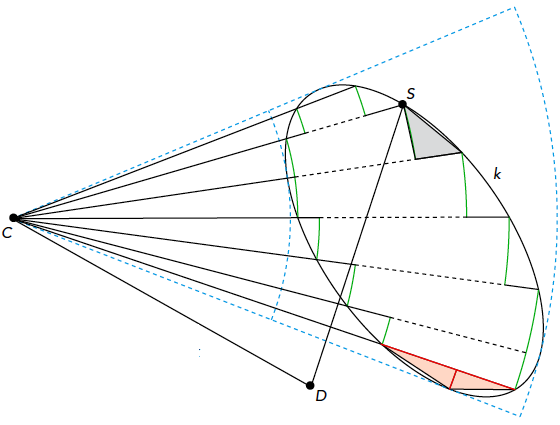
In figuur 5 is een convexe, maar verder volkomen willekeurige, kromme k getekend. Aan het eind van dit stuk zullen we ook concave krommen beschouwen. In de figuur zijn vanuit de pool C zes ‘verschilsectoren’ (verschil van twee cirkelsectoren met gelijke hoeken bij C en verschillende stralen) getekend. Verder gebruiken we het woord ‘sector’. Van deze sectoren weten we hoe we de oppervlakte moeten bepalen met de planimeter, zoals zojuist besproken. De zes sectoren vullen de door de kromme omsloten oppervlakte voor een groot deel. Door steeds meer van deze sectoren te nemen, nadert de totale oppervlakte van al deze sectoren bij elkaar steeds dichter tot de echte oppervlakte, omsloten door k.

We gaan nu als volgt te werk. We beginnen met S in een hoekpunt van een sector en stellen de stand van het geijkte wiel op 0. Dan doorlopen we tegen de klok in de vier zijden van die sector. Dan geeft het wiel de oppervlakte daarvan aan. Vervolgens gaan we met S via een willekeurige weg naar een hoekpunt van een volgende sector. Vanuit dat punt doorlopen we de vier zijden die sector weer tegen de klok in. Dan gaan we via exact dezelfde willekeurige weg weer terug naar het eerste punt waar S begon. Die willekeurige weg hebben we twee keer in tegenovergestelde richtingen doorlopen. Die hebben dus twee keer dezelfde draaiing gegeven, maar tegengesteld. Die hebben elkaar dus opgeheven. Maar de rondgang om de tweede sector heeft de oppervlakte daarvan bij die van de eerste sector in de uitslag van het meetwiel opgeteld. Het wiel geeft nu dus de som van twee oppervlaktes aan.

Vervolgens gaan we via een willekeurige weg naar een hoekpunt van een derde sector, lopen rond en keren via dezelfde weg terug naar het startpunt van S. De stand van het wiel geeft dan de som van drie oppervlaktes aan. Net zo doen we met alle volgende sectoren. Uiteindelijk zijn we weer in het startpunt van S en hebben we de totale oppervlakte van het gebied binnen de gehoekte lijn op het meetwiel staan. Op het meetwiel staat dan het aantal omwentelingen, maar met onze ijking weten we dan meteen de echte oppervlakte.

Dit is natuurlijk een nogal gekunstelde manier en maakt zeker nog niet duidelijk dat je met alleen het rondlopen van de echte kromme k hetzelfde bereikt. Maar kijk eens naar een gestippeld stukje tussen twee aangrenzende sectoren. Dat is twee keer in tegenovergestelde richting doorlopen. De bijdrage van deze stukjes is dus 0. Die stukjes hadden we net zo goed niet kunnen doorlopen. Hetzelfde geldt voor de andere gestippelde stukjes die dubbel doorlopen worden. Bovendien geldt dat de willekeurige wegen (om telkens weer naar een andere verschilsector te gaan) ook geen bijdrage hebben geleverd en dus ook overgeslagen hadden kunnen worden. De conclusie is dan dat we door, vanuit het beginpunt van S, alleen de zwarte gehoekte lijn te doorlopen, alle sectoroppervlaktes samen op het meetwiel aflezen na terugkomst in het beginpunt van S.

Naar een gehoekte lijn met steeds meer hoekjes

Met een beperkt aantal sectoren zijn we er natuurlijk nog niet. Zoals we al opmerkten, kunnen we het aantal sectoren steeds groter maken, met steeds kleinere hoekjes bij C. Dan krijgt de gehoekte lijn steeds meer hoekjes en nadert de waarde op het wiel steeds meer naar de echte oppervlakte. We moeten daarvoor nog wel het volgende opmerken. Wat we aan oppervlakte nog te weinig hebben, bestaat uit een groot aantal ‘driehoekjes’ buiten de gehoekte lijn en binnen de kromme k. De meeste zijn rechthoekig. Als dat niet zo is, zoals in het gekleurde driehoekje onder in k, kan het in twee rechthoekige driehoekjes gesplitst worden door tijdens de passage bij dat punt even heen en weer te gaan naar de kromme k (bijdrage toch 0). Bekijk zo’n driehoekje in figuur 6.

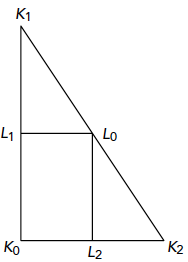
De kromme tussen $K_1$ en $K_2$ is recht gemaakt, omdat dat mag bij steeds grotere aantallen sectoren. Bij elke verdubbeling van het aantal verschilsectoren wordt het aantal driehoekjes twee keer zo groot: van één naar twee in figuur 6. Maar elk driehoekje wordt in oppervlakte vier keer zo klein, omdat de rechthoek $K_0L_2L_0L_1$, met een oppervlakte van de helft van $ΔK_0K_2K_1$, binnen de gehoekte lijn komt te liggen en dus door het meetwiel meegemeten wordt. Dus de ruimte tussen de gehoekte lijn en de kromme k wordt bij een verdubbeling van het aantal verschilsectoren twee keer zo klein. Dat verschil gaat dus na steeds meer verdubbelingen in de limiet naar nul toe en dan hebben we met de gehoekte lijn (waarvan elk punt dus vrijwel op de kromme k ligt) dus de oppervlakte binnen k op ons meetwiel staan.

Van de gehoekte lijn naar de kromme k

Maar toch wringt hier nog iets. Bij het nemen van de limiet blijft de gehoekte lijn altijd een gehoekte lijn en schuif je bij elk minuscule driehoekje over de twee rechthoekszijden in plaats van over de kromme k. Verandert er nog iets als je werkelijk over de kromme k schuift? Vast niet, maar we moeten dat nog wel even precies duidelijk maken. Neem eens zo’n uiterst klein driehoekje:$ ΔK_0K_2K_1$ in figuur 7. Hierin zijn $K_1K_0$ en $K_0K_2$ de twee rechthoekszijden, waarbij de pijlen de richting van schuiven aangeven. De pijl $K_1K_2$ ligt langs de kromme. We kunnen die recht nemen, omdat het driehoekje extreem klein is.

Een belangrijk punt om op te merken is dat bij de drie pijlen de richting van het wiel W steeds dezelfde is, juist omdat we met een extreem klein driehoekje te maken hebben. We hebben de richting van W willekeurig gekozen. Bij passage van $K_1$ naar $K_0$ is de hoek die de loodlijn op W maakt met $K_1K_0$ gelijk aan α. Voor de verandering $w_{10}$ op het meetwiel langs $K_1K_0$ krijgen we dan (zie figuur 3): $$w_{10} = K_1K_0 · sin(α) = K_0L_1 = L_0L_2.$$ Op dezelfde manier krijgen we voor de verandering $w_{02}$ (de hoek is nu $\frac{1}{2} π – α$): $$w_{02} = K_0K_2 · sin(\frac{1}{2} π – α) = L_0K_2.$$ En voor de passage langs de kromme van $K_1$ naar $K_2$ moeten we hoek β nemen. Voor $w_{12}$ krijgen we dan: $$w_{12} = K_1K_2 · sin(β) = L_2K_2.$$ Over $K_1K_0$ loopt het wieltje de ene kant op (die kant nemen we negatief) en van $K_0$ naar $K_2$ en direct van $K_1$ naar $K_2$ loopt het de andere kant op (positief). In de tekening is nu te zien dat de draaiing van het wieltje via de rechthoekszijden gelijk is aan $L_0K_2 – L_0L_2 = L_2K_2$. En dit is precies gelijk aan de draaiing van het meetwiel bij beweging langs kromme k van $K_1$ naar $K_2$. Daarmee is bewezen dat via een rondgang langs k zelf uiteindelijk de oppervlakte binnen k op het meetwiel staat.

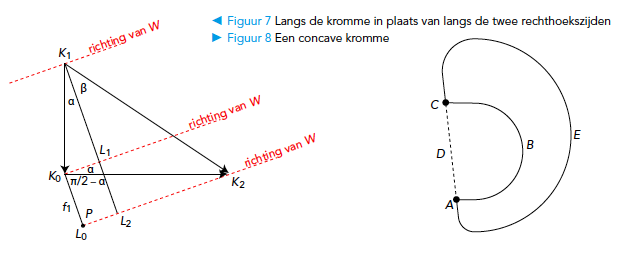
Concave krommen

We kunnen de oppervlakte, ingesloten door een concave kromme, uitrekenen door de figuur in een convexe oppervlakte in te sluiten. Bekijk bijvoorbeeld de concave kromme AECBA in figuur 8. Door A met C te verbinden krijgen we twee convexe krommen ABCDA en AECDA.

Dan geldt voor het volgen (met de punt van de planimeter) van de concave kromme: $$AECBA = AEC + CBA = $$ $$AEC + CA + AC + CBA = AECDA + ADCBA.$$ De toevoeging van CA + AC mag, want die geeft in totaal 0. Hierin is verder AECDA de oppervlakte van de grote convexe kromme en ADCBA minus de oppervlakte van de kleine convexe kromme (negatief, omdat de rondgang met de kok mee is). Samen leveren ze dus de oppervlakte van de concave kromme.

Er zijn natuurlijk nog vele andere complexe situaties denkbaar. Maar die hebben één ding gemeen: ze zijn alle op te delen volgens het bovenstaande voorbeeld.