Als je er goed over nadenkt is 'het aantal elementen' van een verzameling $V$ per definitie dat natuurlijke getal $n$ waarvoor er een één-op-één koppeling tussen $V$ en de verzameling $\{1, 2, \dots, n\}$ bestaat. Ieder element van $V$ wordt aan één getal uit $\{1, 2, \dots, n\}$ gekoppeld en omgekeerd. Tellen is dan gedefinieerd als 'het vinden van de juiste $n$ en een bijbehorende één-op-één koppeling'. En dit werkt voor iedere verzameling $V$ met een eindig aantal elementen.

Oneindig grote verzamelingen

In dit artikel gaan we het niet hebben over verzamelingen zoals $A$ en $B$, maar over oneindig grote verzamelingen. We beginnen met de vraag: hoe verhouden de aantallen elementen van $\mathbb{N}$ en $\mathbb{Z}$ zich tot elkaar? Een eerste antwoord dat ik vaak krijg als ik deze vraag stel, is dat "er natuurlijk ongeveer twee keer zoveel elementen in $\mathbb{Z}$ zitten", omdat er voor ieder positief element $n \in \mathbb{N}$ twee elementen $n$ en $-n$ in $\mathbb{Z}$ zijn. Zolang je eindige verzamelingen bekijkt gaat deze redenering op: het aantal elementen in $\{-20, -19, \dots, 0, \dots, 19, 20\}$ is bijvoorbeeld $\frac{41}{21}$ keer het aantal elementen in $\{0, \dots, 19, 20\}$ en in het algemeen heeft de verzameling $\{-N, -N+1, \dots, 0, \dots, N-1, N\}$ een factor $\frac{2N+1}{N+1}$ , dus ongeveer twee, maal zoveel elementen als $\{0, \dots, N-1, N\}$. Logisch om dan de limiet voor $N \to \infty$ te nemen, nietwaar?

Maar dat is precies waar het lastig wordt om over de grootte van een verzameling of het aantal elementen na te denken. De hierboven beschreven definitie werkt niet, want al tellend zul je voor een verzameling met oneindig veel elementen nooit een laatste element bereiken, en dus ook geen getal $n$ vinden dat 'het aantal elementen' weergeeft. Oneindig is een moeilijk definieerbaar begrip. Wiskundigen, filosofen en theologen hebben zich er eeuwenlang het hoofd over gebroken en er zelfs polemische discussies over gevoerd. Is er een grootste getal? Bestaat er iets groters dan oneindig? Hoeveel is oneindig plus een? Hoeveel is oneindig plus oneindig? De laatste vraag heeft alles te maken met het vergelijken van de aantallen elementen in $\mathbb{N}$ en $\mathbb{Z}$.

Aftelbaar oneindig

Euclides en tijdgenoten hadden duidelijk al over het begrip oneindig nagedacht, want Euclides bewees rond 300 v.Chr. in zijn Elementen dat er oneindig veel priemgetallen zijn: "meer dan welk eindig aantal dan ook." Galileo Galilei schreef in 1638 dat oneindig groot en oneindig klein ons eindige verstand te boven gaan. David Hilbert zei in 1926: "Het oneindige heeft, meer dan elke andere vraag ooit heeft gedaan, het gemoed van de mensen diep beroerd en een enorm stimulerende en vruchtbare invloed op de menselijke geest gehad; het oneindige heeft echter ook, meer dan ieder ander begrip, behoefte aan opheldering." Georg Cantor kwam eind 19e eeuw als eerste met een consistente theorie over oneindigheid en was ook de eerste die zich realiseerde dat er verschillende soorten oneindig bestaan. Hierover kun je in Pythagoras 57-4 lezen: in een brief aan Dedekind vroeg Cantor vrij vertaald of "de twee oneindige verzamelingen $\mathbb{N}$ en $(0, 1)$ 'evenveel elementen' hebben." Het bijzondere was dat Cantor niet tevreden was met "ze hebben allebei oneindig veel elementen, dus ja". Hij wilde weten of er een één-op-één koppeling tussen de elementen van beide verzamelingen was. Cantors uiteindelijke antwoord op de vraag was "nee".

Volgens de inmiddels algemeen aanvaarde theorie van Cantor zijn de verzamelingen $\mathbb{N}$ en $\mathbb{Z}$ wèl even oneindig; ze zijn beide aftelbaar. Dat wil zeggen dat je alle elementen kunt tellen. Ofwel, je kunt ze rangschikken en ze dan een voor een aflopen. Cantor bedacht een label voor 'het aantal elementen' van dergelijke verzamelingen: $\aleph_0$ , gebruikmakend van de eerste letter $\aleph$ (aleph) van het Hebreeuwse alfabet.

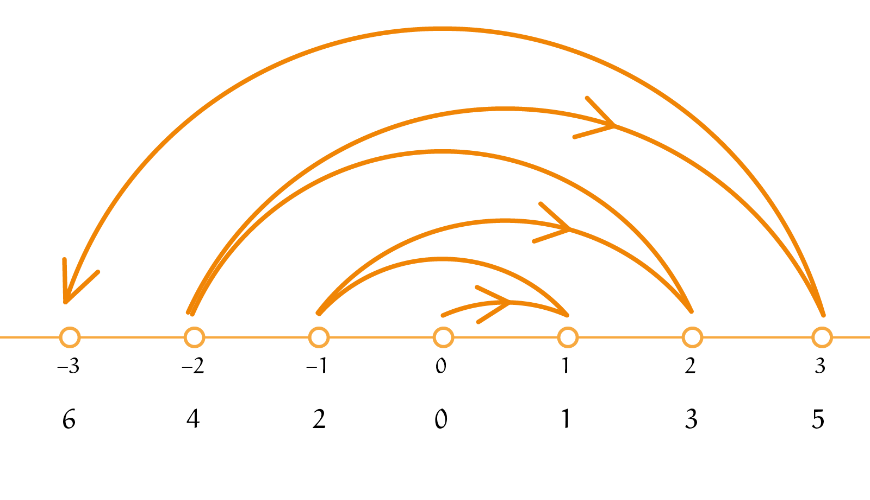
Dat we $\mathbb{N}$ aftelbaar noemen, is niet verrassend, want $\mathbb{N}$ bevat precies alle getallen $n$ die we gebruiken om te tellen. Iedere andere verzameling $V$ noemen we aftelbaar als er een zogenaamde bijectie $f$ tussen $V$ en $\mathbb{N}$ bestaat: $f$ is inverteerbaar, voor iedere $n \in \mathbb{N}$ is er een unieke $v \in V$ zodat $f(v) = n$, en omgekeerd is er voor iedere $v \in V$ een unieke $n \in \mathbb{N}$ zodat $f^{-1}(n) = v$. Een bijectie is precies de één-op-één koppeling van Cantor. De verzameling $\mathbb{Z}$ kunnen we bijvoorbeeld aftellen volgens het patroon in figuur 1.

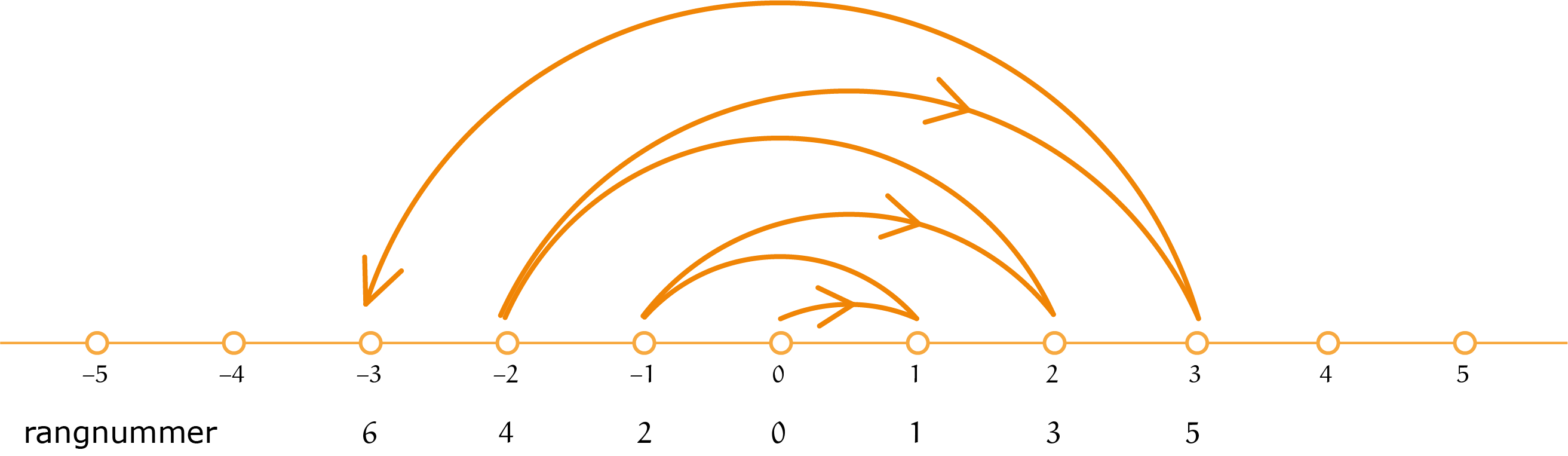
Dit kan beschreven worden met de bijectie

$$f:\mathbb{Z}\to\mathbb{N}:f(z)=\begin{cases}
 2z-1& {\rm\ voor\ } z > 0\\
 -2z & {\rm\ voor\ } z \le 0 
\end{cases}$$

$$f^{-1}:\mathbb{N}\to\mathbb{Z}:f^{-1}(n)=\begin{cases}
 \tfrac{1}{2}(2+1)& {\rm\ voor\ oneven\ } n\\
 -\tfrac{n}{2} & {\rm\ voor\ even\ } n 
\end{cases}$$

Of korter:

$$f^{-1}:\mathbb{N} \to \mathbb{Z}: f^{-1}(n)=(-1)^{n+1}\left(\frac{n}{2}+\frac{1-(-1)^n}{4}\right).$$

De crux blijkt hem dus in het rangschikken te zitten. Hiervoor moesten we de oorspronkelijke, geordende structuur van $\mathbb{N}$ en $\mathbb{Z}$ overboord gooien. Die structuur maakt dat $\mathbb{Z}$ twee keer zoveel elementen lijkt te hebben als $\mathbb{N}$. Maar als je alle gehele getallen bij elkaar op een hoop veegt en hetzelfde doet met de natuurlijke getallen, dan is het minder duidelijk hoe de aantallen elementen zich verhouden, en sta je open voor een andere conclusie dan degene die in eerste instantie voor de hand lijkt te liggen.

De verzameling $\mathbb{Q}$

Verrassend genoeg kun je ook alle elementen van $\mathbb{Q}$ tellen, en heeft die verzameling dus evenveel elementen als $\mathbb{N}$ en $\mathbb{Z}$. Met andere woorden, er zijn evenveel rationale getallen als gehele getallen. Ook hier klopt intuïtief op het eerste gezicht niets van, want alleen tussen $0$ en $1$ zijn er al oneindig veel getallen van de vorm $\frac{1}{n}$ met $n \in \mathbb{Z}^+$.

Je kunt een bijectie tussen de verzamelingen $\mathbb{N}$ en $\{0\} \cup \{\frac{1}{n} | n \in \mathbb{Z}^+\}$ opschrijven en dus zijn die verzamelingen even groot. Dat betekent dat ook $\mathbb{Q}$ aftelbaar is. Een bekende manier om alle elementen van $\mathbb{Q}$ te rangschikken is de volgende. Stel ieder element $\frac{p}{q}\in \mathbb{Q}$ voor door een roosterpunt $(p, q)$, waarbij $p \in \mathbb{Z}$ en $q \in \mathbb{Z}^+$. Vervolgens maak je een pad van een soort tentjes die steeds groter worden en geef je ieder volgend roosterpunt op het pad het volgende rangnummer. Dit pad komt langs alle roosterpunten, en dus krijgt ieder element $\frac{p}{q} \in \mathbb{Q}$ uiteindelijk een rangnummer. Zie het algoritme in figuur 2. De rode nummers zijn de rangnummers bij roosterpunten $(p,q)$.

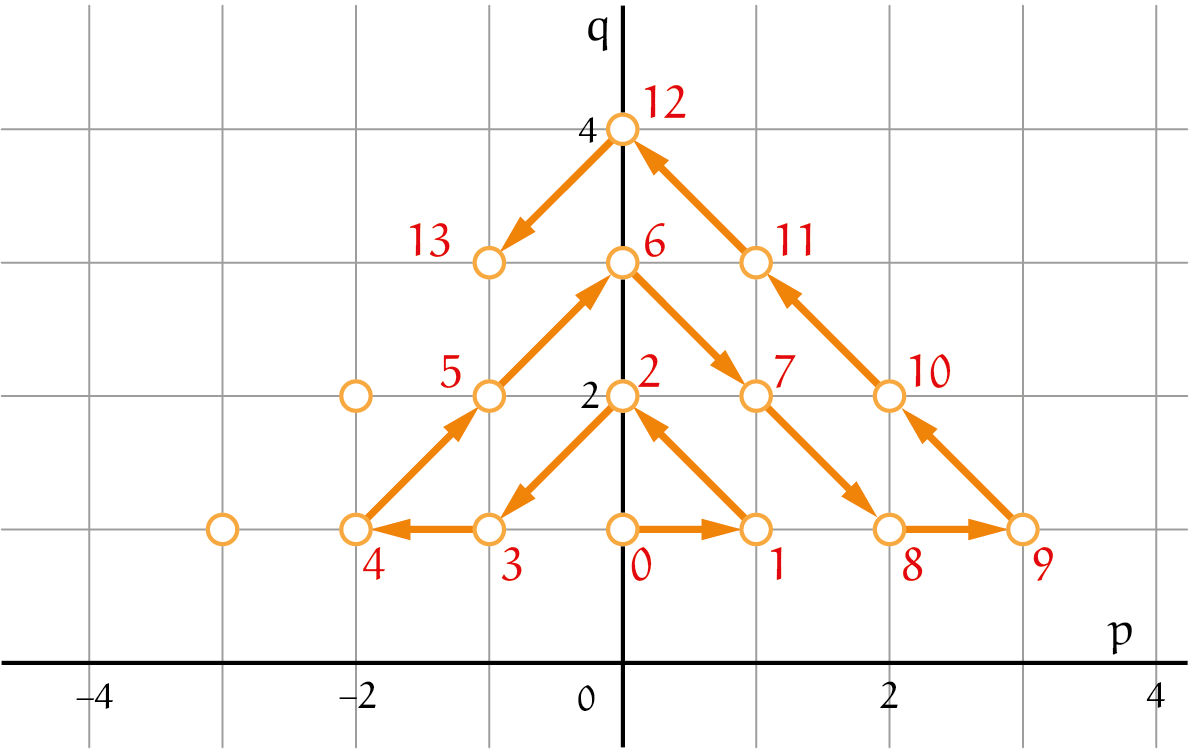
Opgave Maak een lijst met de eerste 40 breuken die je met dit algoritme krijgt. Zitten er getallen bij die meerdere keren voorkomen?

 

Hoewel deze methode vaak als bewijs voor de aftelbaarheid van $\mathbb{Q}$ wordt gebruikt, is er een aspect dat minder fraai is: zoals je gemerkt zult hebben zijn er heel veel dubbeltellingen. Ieder getal in $\mathbb{Q}$ komt enorm vaak (oneindig vaak!) voor in de rij. Het getal $\frac{1}{2}$ komen we bijvoorbeeld tegen als $\frac{1}{2}$ bij roosterpunt $(1, 2)$, maar ook als $\frac{2}{4}$ bij roosterpunt $(2, 4)$ en $\frac{3}{6}$ bij roosterpunt $(3, 6)$.Enzovoorts. Hierop zullen we in een volgend nummer van Pythagoras terugkomen.