De priemgetallen zijn de bouwstenen van de natuurlijke getallen, zeggen we wel eens. De priemgetallen zijn de natuurlijke getallen verschillend van $1$ die enkel zichzelf en $1$ als deler hebben, en je kan er inderdaad elk ander natuurlijk getal mee 'bouwen' via de vermenigvuldiging. Meer nog, elk natuurlijk getal (behalve $0$ en $1$) is op precies één manier te schrijven als een product van priemgetallen, de zogenaamde priemfactorenontbinding. Zo hebben we bijvoorbeeld dat $473 = 11 \cdot 43$ en $2025 = 3^4 \cdot 5^2$. Op precies één manier als we afspreken dat je gelijke priemfactoren moet schrijven als macht en dat de priemfactoren van klein naar groot moeten staan.

Opgave 1 Bovenstaande verklaart waarom we het getal $1$ niet opnemen in de verzameling van de priemgetallen. Hoe?

Priemgetallen blijken sinds de komst van de computer onverwachte praktische toepassingen te hebben, o.a. op het gebied van beveiliging van bankgegevens. Het zijn niet zozeer de priemgetallen op zich die daarbij een grote rol spelen, maar meer het onhandelbare aan die priemgetallen. Van bouwstenen mag je verwachten dat ze goed hanteerbaar zijn, de priemgetallen zijn dat niet. En het belangrijkste probleem dat ze hebben, is dat er geen echt goede manier is om na te gaan of een getal een priemgetal is, of, een gerelateerd probleem, om de priemfactoren van een getal te bepalen. Recent nog, op 12 oktober 2024, kwam in het nieuws dat er een nieuw grootste priemgetal is gevonden, namelijk:

$$2^{136\,279\,841}-1,$$

een getal met $41\,024\,320$ cijfers. Voor de berekeningen hierbij werden duizenden computers verdeeld over 17 landen gebruikt. Eenvoudig is het niet.

De stelling van Wilson Nochtans is er een prachtige stelling beschikbaar waarvan je zou kunnen denken: meer heb je toch niet nodig om na te gaan of zo'n getal priem is of niet? Het gaat om de stelling van Wilson. Deze stelling was al bekend rond het jaar 1000, we vinden ze terug in geschriften van de Arabische wiskundige Alhazen (965-1040), maar ze staat op naam van de Brit John Wilson (1741-1793). Het eerste bewijs ervan werd gegeven door Joseph-Louis Lagrange (1736-1813), in 1771.

De stelling van Wilson
Een natuurlijk getal $p > 1$ is een priemgetal als en alleen als het product $2 \cdot 3 \cdot 4 \cdot \dots \cdot (p-2) \cdot (p - 1) + 1$ deelbaar is door $p$.

Toegepast voor $p = 6$: $6$ is geen priemgetal want $2 \cdot 3 \cdot 4 \cdot 5 + 1 = 121$ is niet deelbaar door $6$.

Voor $p = 7$: $7$ is een priemgetal want $2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 + 1 = 721$ is (duidelijk) deelbaar door 7.

Een kant-en-klaar criterium om te checken of een getal priem is!

We kunnen deze stelling ook anders formuleren, door gebruik te maken van modulorekenen en de faculteitnotatie:

$p > 1$ is priem $\Leftrightarrow (p - 1)! \equiv -1\ (mod\ p)$

waarbij we voor een geheel getal $n$ noteren $n! = n \cdot (n - 1) \cdot \dots \cdot 2 \cdot 1$ (lees 'n faculteit') en waarbij $a \equiv b\ (mod\ p)$ aangeeft dat $a - b$ deelbaar is door $p$, oftewel $a$ en $b$ hebben dezelfde rest bij deling door $p$. (Lees hiervoor het artikel Modulo Benjamin in Pythagoras 64-5.)

We bewijzen nu de stelling. En dat doen we in stappen.

Deel 1 van het bewijs

Eerst tonen we het volgende aan:

Als $p > 1$ geen priemgetal is, dan geldt dat $(p - 1)! \equiv -1\ (mod\ p)$.

Dat is het gemakkelijke deel. Want als $p$ geen priemgetal is, en dus een product van priemgetallen (met meer dan één factor), dan zitten alle factoren van $p$ in het product $(p - 1)!$. We bekijken dit aan de hand van een voorbeeld. Neem $p = 90 = 2 \cdot 3^2 \cdot 5$. We zien 3 factoren, namelijk $\color{red}{2}$, $\color{red}{9}$ en $\color{red}{5}$ en die zijn natuurlijk allemaal kleiner dan $90$. Maar we hebben nu:

$$(90 - 1)!=$$

$$\color{red}{2} \cdot 3 \cdot 4 \cdot \color{red}{5} \cdot \dots \cdot 8 \cdot \color{red}{9} \cdot 10 \cdot \dots \cdot 88 \cdot 89$$

Elk van die factoren van $90$ zit in $89!$, dus $89!$ is deelbaar door $90$. Dit is altijd waar als $p$ geen priemgetal is (behalve voor $p = 4$, bij dit ene kwadraat gaat bovenstaande redenering niet op). We hebben in het algemeen:

Als $p > 4$ geen priemgetal is,
dan is $(p - 1)!$ deelbaar door $p$,
oftewel $(p - 1)! \equiv 0\ (mod\ p)$
(en dus niet congruent met $-1$).

Voorbereidend werk voor deel 2 van het bewijs

Om nu te bewijzen dat $(p - 1)!$ wel congruent is met $-1\ (mod\ p)$ voor een priemgetal $p$, zullen we een voorstelling gebruiken voor het product van 2 getallen $(mod\ p)$. Deze voorstelling vinden we bij het weven van satijn (zie tekstkader verderop).

We gaan als volgt te werk voor bijvoorbeeld $p = 5$. We kunnen de veelvouden van een vast getal $a$ (de stapgrootte genoemd) voorstellen in een rechthoek met basis $5$ en hoogte $5 \cdot a$ (zie links in figuur 1, hier voor $a = 2$):

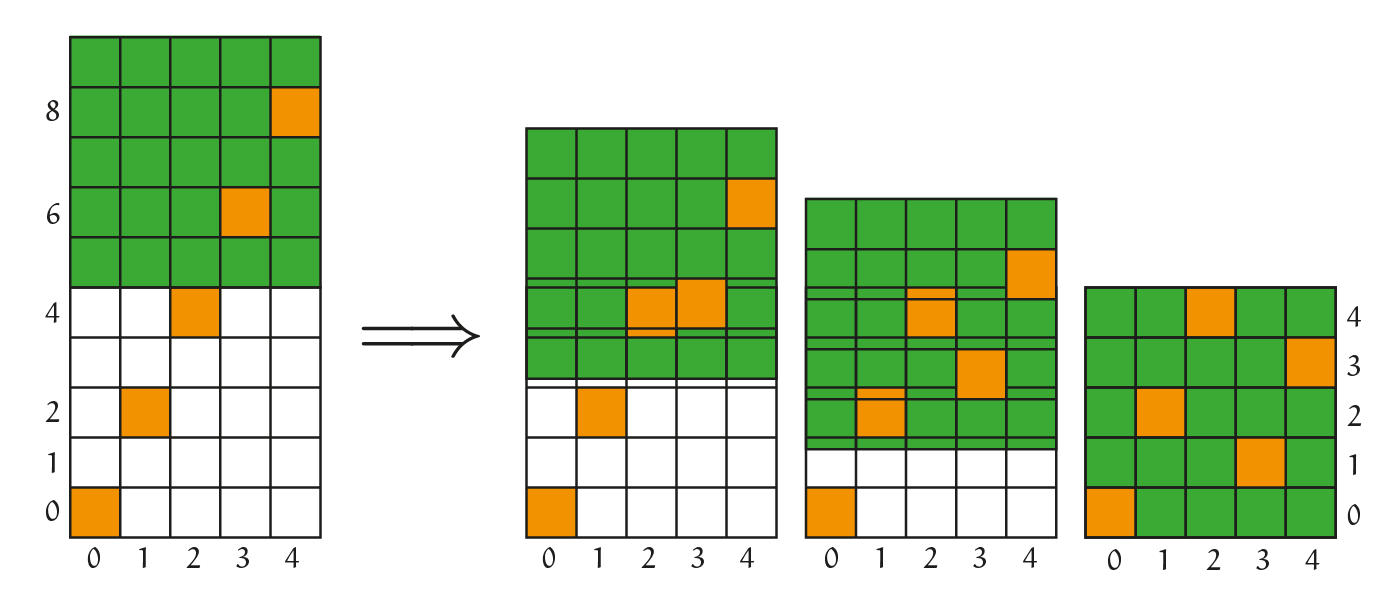
We nummeren de rijen en de kolommen zoals in de figuur. We starten met het inkleuren van het vierkantje linksonder, en gaan dan telkens $1$ stap naar rechts en $2 (= a)$ naar boven. De hoogte van het ingekleurde vierkant in kolom $i$ is dan precies gelijk aan $i \cdot a$. Daarna verdelen we in vierkanten van $5$ op $5$ en schuiven deze over elkaar zoals op de figuur. Het resultaat is het $5$ op $5$ vierkant met stapgrootte $2$ uit het tekstkader. De hoogte van het ingekleurde vierkant in de $i$-de kolom in de meest rechtse figuur is dus gelijk aan $i \cdot a\ (mod\ 5)$.

Opgave 2 Neem $p = 5$ en $a = 3$, vertrek van een rechthoek met basis $5$ en hoogte $15$, en herhaal het vorige procedé. Schuif de drie boven elkaar liggende vierkanten van $5$ op $5$ over elkaar heen. Wat is het resultaat?

We kunnen nu zo'n vierkant maken voor elke waarde van $p$ en voor $a = 1, 2, \dots, p - 1$. En met zo'n vierkant kunnen we aan modulorekenen doen. Neem bijvoorbeeld het vierkant met zijde $p = 11$ en met stapgrootte $a = 3$:

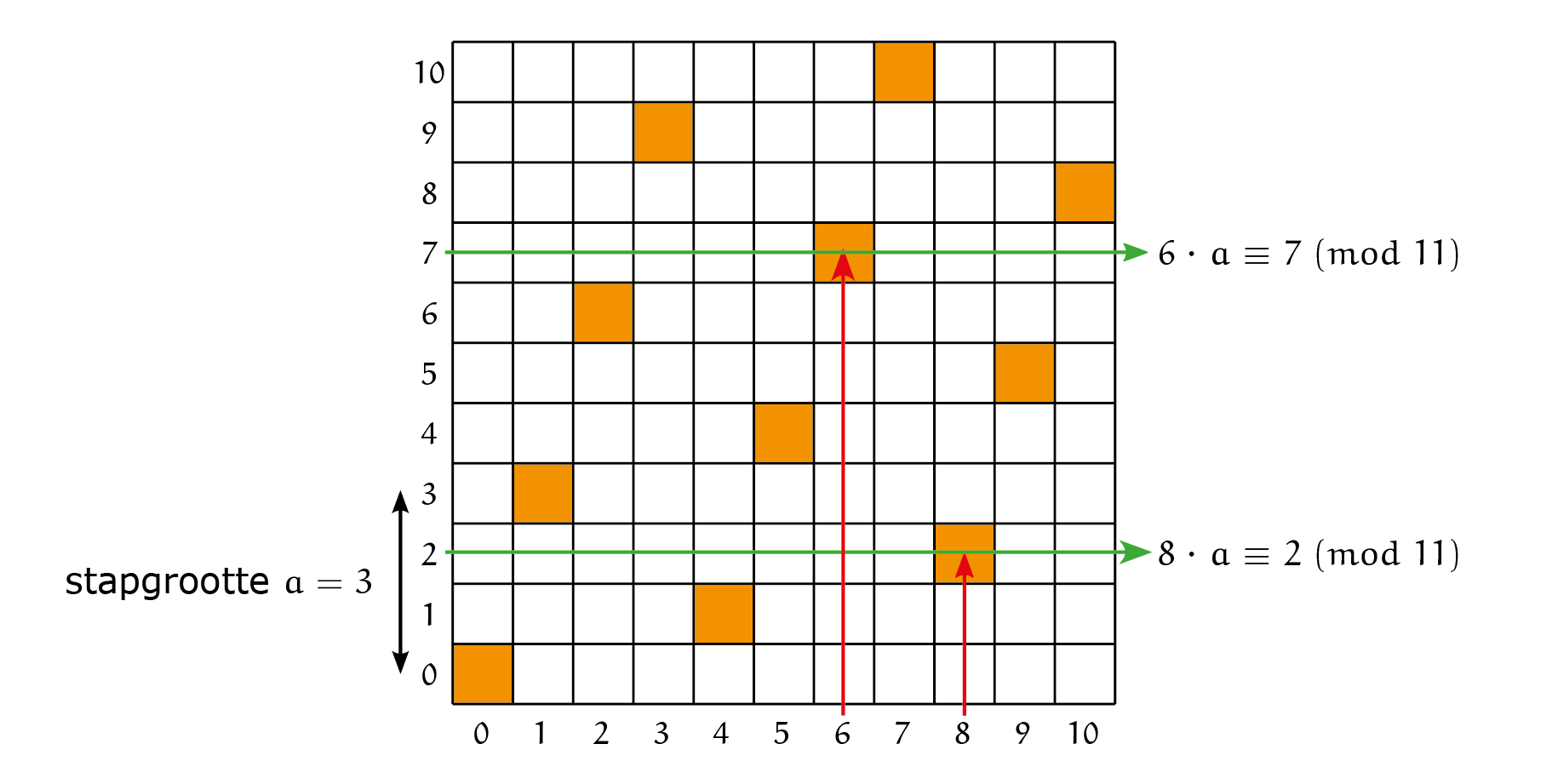
In figuur 2 zie je hoe je de waarde van elk van de producten $i \cdot a$ kan aflezen.

Deel 2 van het bewijs

Nu zijn we klaar om het volgende aan te tonen: Als $p > 1$ een priemgetal is, dan geldt dat $(p - 1)! \equiv -1\ (mod\ p)$. Als voorbeeld nemen we $p = 7$. En we tekenen de bijhorende vierkanten voor $a=1, 2, 3, 4, 5, 6$.

We stellen het volgende vast.

• Omdat de zijde van het vierkant een priemgetal is, zie je in bovenstaande vierkanten in elke rij en elke kolom precies 1 ingekleurd vierkantje (zie opgave in tekstkader).
• Dat heeft als gevolg dat er bij elke stapgrootte precies 1 ingekleurd vierkantje op de rij met nummer $1$ staat (die hebben we rood gekleurd). Bijvoorbeeld bij $a = 2$ staat dat in kolom $4$ (herinner je: kolommen worden genummerd vanaf $0$). We weten uit het vorige dat dit betekent dat $4 \cdot 2 \equiv 1\ (mod\ 7)$. Omdat $4 \cdot 2 = 2 \cdot 4$ staat het rode vierkantje bij $a = 4$ dan natuurlijk in kolom $2$.
• Zo kunnen we de stapgroottes $2$ per $2$ combineren: bij elke stapgrootte $a$ hoort er een stapgrootte $b$ zodat $a \cdot b \equiv 1\ (mod\ 7)$. 
• De bij elkaar horende $a$ en $b$ zijn verschillend behalve voor $a = 1$ en voor $a = p - 1$.

In figuur 3 hebben we de bij elkaar horende $a$ en $b$ aangeduid.

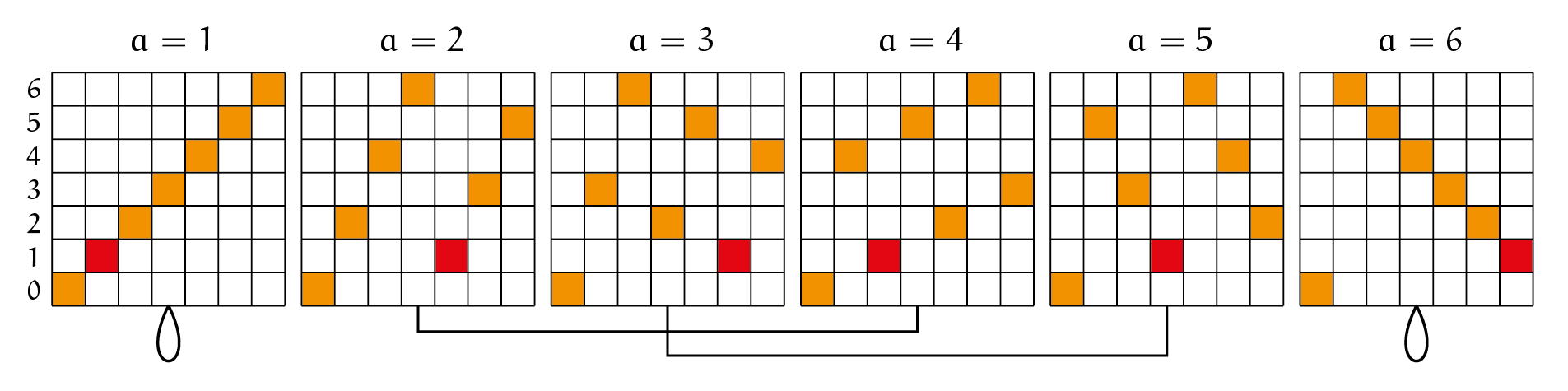
Dit blijkt altijd zo te zijn, voor elk priemgetal $p$. En daarmee kunnen we het bewijs afwerken.

Eerst doen we dat voor $p = 7$: $6! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 = 1 \cdot (2 \cdot 4) \cdot (3 \cdot 5) \cdot 6$.

Wat tussen de haakjes staat is gelijk aan $1$ modulo $7$. Dus $6! \equiv 1 \cdot 1 \cdot 1 \cdot 6 = 6\ (mod\ 7)$. En $6 \equiv -1\ (mod\ 7)$.

Voor een willekeurige $p$ priem werkt het ook. In de uitdrukking voor $(p - 1)!$ zet je de factoren met product $1\ (mod\ p)$ $2$ bij $2$ bij elkaar. Dan hou je over dat $(p - 1)! \equiv 1 \cdot (p - 1) \equiv -1\ (mod\ p)$.

Besluit

De stelling van Wilson geeft een eenvoudige manier om na te gaan of een getal een priemgetal is, zou je kunnen denken. In theorie is dat inderdaad zo. Maar de stelling is praktisch gezien niet interessant, omdat faculteiten snel groot worden. Om na te gaan of bijvoorbeeld het getal $1009$ een priemgetal is, moet je kijken naar $1008!$, en dat is een getal van $2592$ cijfers! En $1009$ heeft maar $4$ cijfers. Voor het grootste tot nu toe bekende priemgetal uit de eerste paragraaf heeft de faculteit in kwestie meer dan $10^{41\,024\,327}$ cijfers, een onhandelbaar groot getal! Gelukkig zijn er inmiddels betere priemtesten...

		Het weven van satijn Op het einde van de negentiende eeuw ontstond er in Frankrijk een heel nieuwe tak van de meetkunde, de Géometrie plane des tissus of de vlakke meetkunde van de stoffen. Door te verwijzen naar de manieren waarop stoffen geweven worden, slaagde de wiskundige Édouard Lucas (1842-1891) samen met enkele anderen erin om eigenschappen uit de getaltheorie, waar de stelling van Wilson ook toe behoort, aanschouwelijk te maken. Bij het weven van draden tot textiel, worden verticale en horizontale draden met elkaar vervlochten, zoals aan de linkerkant van figuur 4. In het midden zie je hoe het eruitziet als de draden tegen elkaar worden aangeschoven. 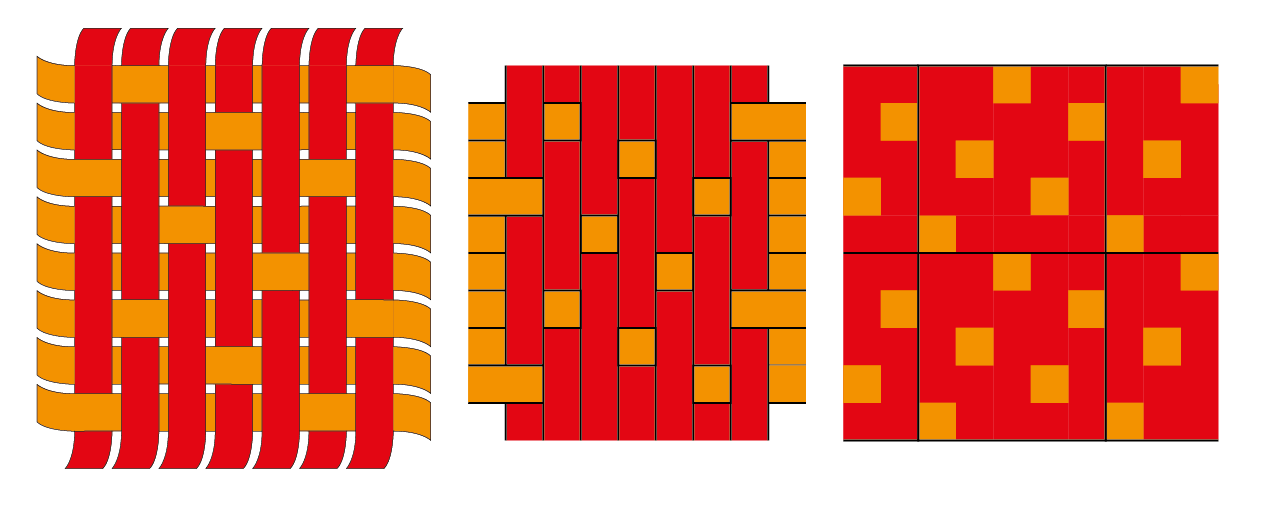Het gaat hier om een zogenaamde satijnbinding. Bij satijn kruisen wat men noemt de kettingdraden (rood) en de inslagdraden (oranje) elkaar op een speciale manier. Als de oranje inslagdraad op een bepaalde plaats boven ligt, dan ligt bij minstens 4 van de volgende kruisingen de rode kettingdraad boven. In de figuur zijn het er precies vier. Op de rechtse figuur zie je een groter stuk van het resultaat. Merk op dat een bepaald patroon zich herhaalt in de beide richtingen, namelijk het gedeelte binnen het vierkant met zwarte rand, dat we in het vervolg zo zullen voorstellen: zoals in figuur 5. Dit patroon wordt als volgt gevormd: we kleuren de linkeronderhoek van het vierkant in, gaan dan één stap naar rechts en (in dit geval) twee naar boven, kleuren weer in, enzoverder. Indien we zo uit het vierkant stappen aan de bovenkant, dan tellen we verder vanaf de onderrand. We hebben in dit geval gewerkt met stapgrootte $2$, maar dat kan evengoed $1$ of $3$ of $4$ zijn. Dan krijgen we respectievelijk de resultaten in zoals in figuur 6. Voor een vierkant van $6$ op $6$ zijn de verschillende mogelijkheden: te zien in figuur 7.   Opgave Neem een blad ruitjespapier en experimenteer met vierkanten van andere groottes. Neem een vierkant met als zijde een getal $m > 1$ dat geen priemgetal is, bijvoorbeeld $m = 12$. Kleur in voor stapgrootte $1, 2, 3, \dots, m-1$. Merk op dat je, zoals bij zijde $6$, stapgroottes hebt waarbij er meer dan één ingekleurd vierkant op dezelfde hoogte ligt. Je kan zelf nagaan dat het om de stapgroottes gaat die een deler $(> 1)$ gemeenschappelijk hebben met het getal $m$. Neem nu een vierkant met als zijde een priemgetal $p$, en kleur in voor de verschillende stapgroottes. Merk op dat er op elke rij en elke kolom precies 1 ingekleurd vierkant ligt.