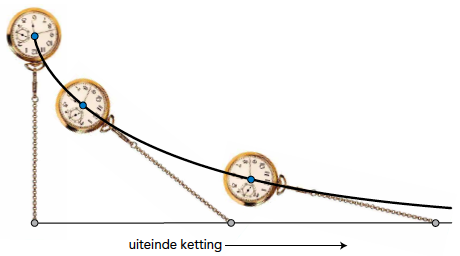
Figuur 1 Welke kromme wordt hier beschreven?

Rond 1670, in een bijeenkomst van de Koninklijke Franse Academie voor Wetenschappen, legde Claude Perrault (het minder bekende broertje van Charles Perrault, schrijver van sprookjes zoals De Schone Slaapster, Assepoester, Klein Duimpje) het volgende probleem voor aan de wetenschappelijke gemeenschap. Hij legde zijn zakuurwerk op tafel (zie figuur 1), met het uiteinde van de ketting op de rand van die tafel, hij trok het uiteinde opzij over de rand van de tafel, en stelde de vraag: wat is de vorm van de kromme die beschreven wordt door dit uurwerk? Het bleek een lastig probleem te zijn, waar onder anderen Isaac Newton en Christiaan Huygens zich op toelegden. Christiaan Huygens vond uiteindelijk in 1693 een vergelijking voor de kromme in kwestie, die hij ‘tractrix’ doopte, van het Latijnse ‘trahere’, wat ‘trekken’ betekent. De kromme bestaat uit twee delen, en ziet er in zijn geheel uit als in figuur 2.

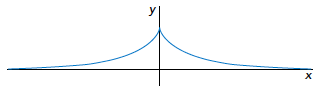
Figuur 2 De tractrix

De vergelijking van de rechter helft van de tractrix wordt gegeven door

$$x =ln(1+ \sqrt{1− y^2} )−ln y − \sqrt{1− y^2} ,$$

waarbij we veronderstellen dat de afstand tussen het uiteinde van de ketting en het midden van de wijzerplaat gelijk is aan $1$. Hoe je hieraan komt, dat kan je nagaan in het kader verderop.

De kromme wordt bij ons ook wel ‘sleepkromme’ genoemd. Lang geleden stond deze kromme eens in dit tijdschrift: zie het artikel ‘De sleepkromme’ van Henk Mulder in Pythagoras 21-5 (te vinden op http://www.pyth.eu). Henk Mulder had een speciaal apparaatje gebouwd om hem te tekenen (zie figuur 3).

Figuur 3 De ‘sleepkromme’ uit Pythagoras 21-5
(maart 1982)

In Duitsland spreekt men ook wel over de Hundkurve (hondkromme), omdat het de weg is die een weerspannige hond aflegt als die door zijn baasje aan zijn leiband wordt voortgetrokken.

Variaties op een thema

Als we nu bijvoorbeeld het uiteinde van de ketting bewegen over een cirkel in plaats van over een rechte, dan krijgen we natuurlijk een andere kromme, die toch wel familie is van de tractrix (zie figuur 4). De resulterende blauwe kromme nadert in de limiet naar een cirkel. Het vinden van een formule voor deze kromme is een stuk lastiger!

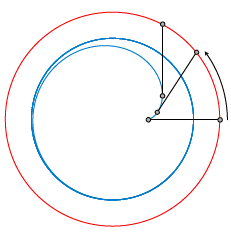
Figuur 4 Een kromme die familie is van de tractrix

De mogelijkheden zijn eindeloos: beweeg het uiteinde van de ketting over een gegeven kromme, en je krijgt een sleepkromme die bij die kromme hoort. Typisch bij dergelijke krommen is dat de ‘ketting’ steeds raakt aan de sleepkromme en dat de afstand gemeten over de raaklijn van het raakpunt tot het punt op de kromme waarover we het uiteinde van de ketting bewegen, constant blijft: het is precies de lengte van de ketting.

Je beseft het misschien niet, maar als je met de fiets rijdt, dan produceer je voortdurend sleepkrommen. Inderdaad, omdat een fiets op twee plaatsen de grond raakt, en de afstand tussen die twee punten constant is, kan je het zo bekijken: als het punt waar je voorwiel de grond raakt een bepaalde kromme beschrijft, dan beschrijft het punt waar je achterwiel de grond raakt ook een kromme, en dat is dus een sleepkromme (zie figuur 5)!

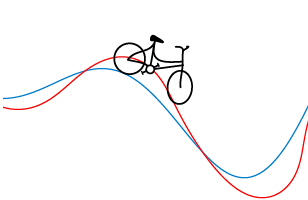
Figuur 5 Al fietsend produceer je vele sleepkrommen

Oppervlakte bij sleepkrommen

In het boek Aha! Insight van puzzelmeester Martin Gardner staat het volgende probleem. Een firma moet vasttapijt leggen in een ringvormige gang van een nieuw vliegveld, en de enige afmeting die ze hebben gekregen is de lengte van een koorde die raakt aan de binnenste cirkel (zie figuur 6, links). Maar de meetkundige van het huis laat al snel weten dat die ene afmeting voldoende is: hij heeft namelijk een formule waar hij dat getal instopt en waar de oppervlakte van het ringvormige gebied uitkomt. Wat is de gezochte oppervlakte?

Om dit probleem op te lossen, kan je als volgt redeneren: blijkbaar hangt de oplossing niet af van de grootte van de twee cirkels die de ring bepalen, maar enkel van de lengte van die koorde. Als we dan de straal van de binnenste cirkel gelijkstellen aan nul en we passen de straal van de buitenste cirkel zo aan dat de koorde in kwestie even lang blijft (zie figuur 6, rechts), dan zal die koorde een diameter zijn van de grote cirkel. De gezochte oppervlakte is dus gelijk aan die van een cirkel met een diameter van $100$ meter.

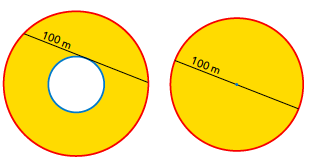
Figuur 6 Hoe groot is het ringvormige gebied?

Mamikon Mnatsakanian

Maar klopt de bovenstaande redenering wel? Om dit te bewijzen, gebruiken we de stelling van Mamikon, die grafisch geïllustreerd in dit geval het volgende zegt: de gelijkgekleurde gebieden in figuur 7 hebben dezelfde oppervlakte.

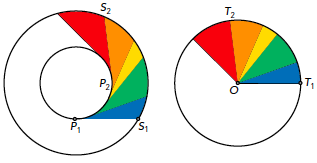
Figuur 7 De stelling van Mamikon: gelijkgekleurde
gebieden zijn even groot

Het verband tussen de linker en de rechter figuur is het volgende. We tekenen een raaklijn in een punt $P$ van de kleine cirkel. Deze raaklijn snijdt de grote cirkel in het punt $S$. We verplaatsen nu dit lijnstuk $PS$ evenwijdig met zichzelf naar de rechter figuur op zo’n manier dat het punt $P$ terechtkomt in $O$. Punt $S$ komt dan terecht in $T$. We laten nu het punt $S$ (links) bewegen over de grote cirkel. Omdat de afstand tussen $P$ en $S$ constant is, liggen de beeldpunten $T$ (rechts) op een cirkel met als straal de afstand van $P$ tot $S$. (In het kader verderop zie je hoe je een soortgelijke techniek kan gebruiken om te bewijzen dat de som van de hoeken van een driehoek gelijk is aan $\pi$.)

We zullen proberen te laten zien waarom die oppervlaktes gelijk moeten zijn. Merk hiervoor op dat de kleine cirkel een sleepkromme is van de grote cirkel: als we met de fiets starten rakend aan de kleine cirkel, en met ons voorwiel over de grote cirkel rijden, dan is het spoor van het achterwiel de kleine cirkel. We willen de oppervlakte berekenen van het gebied tussen beide cirkelvormige sporen.

Nu kan je een cirkel bekijken als een veelhoek met oneindig veel zijden (zie figuur 8). We kijken even wat er precies gebeurt als we in plaats van de kleine cirkel een veelhoek nemen. Je plaatst je fiets op een zijde van de veelhoek, met het achterwiel van de fiets in een hoekpunt ervan. Je rijdt dan over die zijde tot het achterwiel in het volgende hoekpunt staat. Dan draai je je fiets een slag tot je fiets in de richting van de volgende zijde staat, waarbij je ervoor zorgt dat je achterwiel op dat hoekpunt blijft staan: het contactpunt van je voorwiel met de grond beschrijft daarbij een cirkelboog. Dan rij je door tot aan het volgende hoekpunt, enzovoort. Opnieuw zijn er twee sporen (dat zie je best in de rechter figuur: de veelhoek binnenin en de gebroken kromme aan de buitenkant) en die begrenzen een gebied. Het is duidelijk dat de oppervlakte van dat gebied precies de grootte heeft van een volledige cirkel: je kan de cirkel terugvinden door de gekleurde stukjes te verschuiven! Merk ook op dat als je maar een deel van de baan doorloopt, je dan ook de bijhorende oppervlakte kan berekenen. Daarbij is de hoek waarover de raaklijn aan de sleepkromme gedraaid is, bepalend.

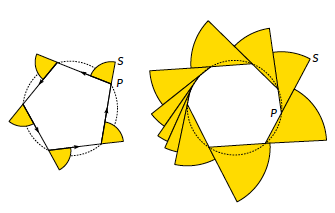
Figuur 8 Om de stelling van Mamikon aan te tonen,
benaderen we de cirkel door een veelhoek

Als we het aantal zijden van de veelhoek vergroten, dan blijft die oppervlakte gelijk. Dus ook in de limiet, dan wordt de veelhoek de kleine cirkel. De oppervlakte tussen de grote en de kleine cirkel is dus precies gelijk aan de oppervlakte van een cirkel met als straal de vaste afstand $d = PS$, dus $\pi d^2$.

Opdracht 1. Je kan dit bewijzen met de stelling van Pythagoras. Veronderstel dat de grote cirkel in figuur 6 straal $R$ heeft en de kleine straal $r$. Bereken met de stelling van Pythagoras de lengte $L = 2d$ van een koorde van de grote cirkel die raakt aan de kleine cirkel. Bereken dan de oppervlakte van het ringvormig gebied, en laat zien dat die oppervlakte gelijk is aan $\pi d^2$.

Ook als we niet te maken hebben met $2$ cirkels, dan nog gaat de redenering op. Stel bijvoorbeeld dat je met de fiets de lus rijdt die in figuur 9 is getekend, dan is de oppervlakte tussen beide krommen opnieuw gelijk aan $\pi d^2$ met d de afstand tussen de twee punten waar je fiets de grond raakt. Je kan nu zelf nagaan dat de oppervlakte tussen de tractrix in figuur 2 en de horizontale as gelijk is aan $\frac{\pi}{2}$.

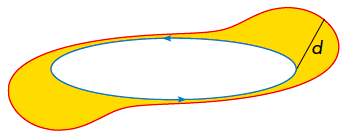
Figuur 9 Sporen van een fiets, de oppervlakte van het gekleurde deel is $\pi d^2$

Opdracht 2. Over welke hoek wordt de ketting hier gedraaid?

De stelling van Mamikon is ook meer algemeen geldig. Belangrijk is wel dat de hoek van de raaklijn blijft toenemen.

Opdracht 3. Zoek een sleepkromme waarbij de hoek van de raaklijn niet blijft toenemen.

Je vindt over deze methode heel wat als je zoekt op het internet naar “the method of sweeping tangents”.

De planimeter van Prytz

Deze methode om een oppervlakte te berekenen is de basis van de planimeter van Holger Prytz, uitgevonden in 1875. Je ziet er een in figuur 10.

Figuur 10 De planimeter van Prytz (met toestemming
overgenomen uit het boek How round is your
circle? van J. Bryant and C. Sangwin)

Met zo’n planimeter kan je de oppervlakte van een vlakke figuur berekenen. Je gaat hiervoor zoals in figuur 10 met de punt over de kromme die de vlakke figuur begrenst. De rest van het toestel wordt dan meegesleept, en je krijgt een sleepkromme. Als je de rand van het gebied volledig hebt doorlopen, dan kijk je naar de stand van het toestel: de horizontale arm zal niet meer in dezelfde richting wijzen als bij de start. Als je de hoek tussen de oorspronkelijke richting en de nieuwe bepaalt, dan krijg je een benadering voor de oppervlakte van het gebied binnen de kromme door die hoek (in radialen) te vermenigvuldigen met $\frac{d^2}{2}$, waarbij d de lengte is van de arm van de planimeter. De lengte van de planimeter is belangrijk: je neemt die best groot ten opzichte van de breedte van het gebied waarvan je de oppervlakte wil bepalen. Meer over planimeters vind je in het artikel ‘De planimeter’ van Jan Guichelaar in het februarinummer van deze jaargang.

Vergelijking van de tractrix

We kunnen de vergelijking van de tractrix ook zelf vinden, en dat wordt net iets eenvoudiger als we hem voorstellen zoals op bijgaande figuur. Indien we ons beperken tot de helft ervan, dan hebben we te maken met een functie, en we zoeken een voorschrift van de vorm $y = f(x)$. Hiervoor bepalen we de raaklijn aan de grafiek van die functie in een willekeurig punt $P$ met coördinaten $(x_0, y_0)$. De vergelijking ervan is gelijk aan $y - f(x_0) = f'(x_0) \cdot (x - x_0)$. Deze raaklijn snijdt de $y$-as in het punt $Q$, en we weten uit de definitie van de tractrix dat de afstand van $P$ tot $Q$ (in dit geval) gelijk is aan $1$. Het punt $Q$ heeft coördinaten $(0, a)$ waarbij uit de vergelijking van de raaklijn volgt dat $$a = f(x_0) – x_0 f'(x_0) .$$ De afstand van $P$ tot $Q$ is dus gelijk aan

$$\sqrt{(x_0 -0)^2 +( f (x_0 )-a)^2} = \sqrt{x_0^2 +x_0^2 ( f ʹ(x_0 ))^2}$$

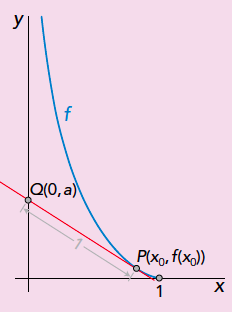
en we weten dat dit $1$ geeft, dus vinden we na kwadrateren:

$$x_0^2 (1 + f'(x_0)^2) = 1.$$

Hieruit kunnen we de afgeleide van $f$ halen, en in een willekeurig punt van de kromme is die dus gelijk aan:

$$f ʹ(x) = − \frac{1−x^2}{x}.$$

Hierbij hebben we bij de worteltrekking rekening gehouden met het feit dat de afgeleide in dit geval negatief moet zijn, zoals je kan zien in de figuur.

Om het voorschrift van $f$ zelf te vinden, moet je nog integreren:

$$f (x) = − \int \frac{1−x^2}{x} dx =$$

$$ln(1+ \sqrt{1−x^2} )−ln x − \sqrt{1−x^2} +C.$$

Hierbij is $C$ een integratieconstante die we kunnen bepalen door op te merken dat het punt met coördinaten $(1, 0)$ op de kromme ligt. Dus $C = 0$ en we vinden de vergelijking terug van in de tekst, maar met $x$ en $y$ omgewisseld.

Opdracht. Ga na dat de afgeleide van bovenstaande functie $f(x)$ gelijk is aan $- \sqrt{1-x^2} / x$.

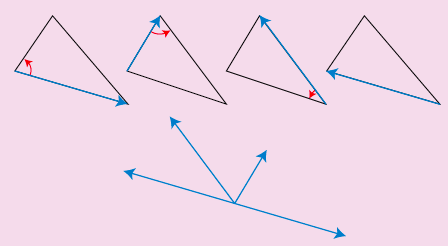
Bewijs zonder woorden

Voor de eigenschap die zegt dat de som van de hoeken (in radialen) van een driehoek gelijk is aan $\pi$.