Als de decimalen in een breuk zich gaan herhalen, noteren we dat zich herhalende deel met een streep eronder, dus $3/11 = 0{,}\underline{27}$ of $207/312
= 0{,}663\underline{461538}$. En omdat we alleen in het gedeelte na de komma geïnteresseerd zijn, kijken we alleen naar breuken die tussen $0$ en $1$ liggen: de teller is kleiner dan de noemer. 

De lengte van de zich herhalende groep cijfers hangt af van de noemer van de breuk, die noemen we, uiteraard, $N$. Ten eerste: die lengte is nooit groter dan $N - 1$. En verder is het alleen bij priemgetallen mogelijk (maar niet gegarandeerd) dat de lengte van $N - 1$ ook echt gehaald wordt. En ook geldt dat je bij priemgetallen niet hoeft
te wachten: de herhaling begint meteen.

We bekijken de eerste priemgetallen en nemen $1$ als teller: $1/2 = 0{,}5$, $1/3 = 0{,}\underline{3}$, en $1/5 = 0{,}2$. De priemgetallen $2$ en $5$ zijn de priemdelers van $10$ en geven ons nullen aan het eind. En bij $3$ zien we dat de lengte van de groep $1$ is en dat is kleiner dan $2$; dus inderdaad: $N - 1$ wordt niet altijd gehaald.

Maar bij $7$ gaat het goed: $1/7 = 0{,}\underline{142857}$. En er gebeurt meteen iets interessants, kijk maar naar dit tabelletje

$1/7$		$0{,}\underline{142857}$
$2/7$		$0{,}\underline{285714}$
$3/7$		$0{,}\underline{428571}$
$4/7$		$0{,}\underline{571428}$
$5/7$		$0{,}\underline{714285}$
$6/7$		$0{,}\underline{857142}$

Je ziet het misschien beter als we de rijen wat omgooien:

$1/7$		$0{,}\underline{142857}$
$3/7$		$0{,}\underline{428571}$
$2/7$		$0{,}\underline{285714}$
$6/7$		$0{,}\underline{857142}$
$4/7$		$0{,}\underline{571428}$
$5/7$		$0{,}\underline{714285}$

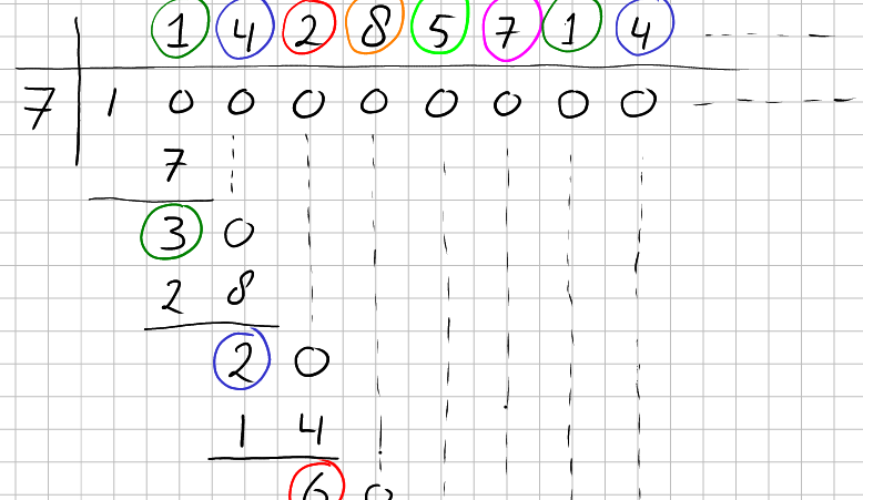
 De groepjes cijfers schuiven telkens één positie op. Dat verschijnsel doet zich altijd voor bij een priemgetal $p$ waar de maximale lengte van $p - 1$ cijfers gehaald wordt. We gaan onderzoeken waarom dat zo is. En dat doen we met behulp van staartdelingen; daar kun je het verschijnsel mooi zien ontstaan. Kijk naar de staartdeling voor $1/7$ in figuur 1.

Het eerste cijfer achter de komma (groen omcirkeld) is wat je krijgt als je $10$ door $7$ 'deelt met rest': het quotiënt is $1$, de rest is $3$ (ook groen omcirkeld). Check: $1 \times 7 + 3 = 10$. De blauw omcirkelde $4$ is het quotiënt van $30$ en $7$, met de ook blauw omcirkelde rest $2$. Check: $4 \times 7 + 2 = 30$. De rood omcirkelde $2$ en $6$ zijn het quotiënt en de rest van $20$ gedeeld door $7 : (2 \times 7 + 6 = 20)$, enzovoort.

Maar de staartdeling doet meer. Er geldt ook dat $14$ het quotiënt bij deling van $100$ (dus $10^2$) door $7$ is met rest $2$. En $142$ en $6$ zijn quotiënt en rest bij  deling van $1000$ (dus $10^3$) door $7$. Dit gaat zo door en we vatten het samen in een tabelletje:

macht		quotiënt		rest
$10^0$		$0$		$1$
$10^1$		$1$		$3$
$10^2$		$14$		$2$
$10^3$		$142$		$6$
$10^4$		$1428$		$4$
$10^5$		$14285$		$5$
$10^6$		$142857$		$1$
$107$		$1428571$		$3$
$108$		$14285714$		$2$

De eerste rij geeft weer dat je bij het delen van $1$ door $7$ als quotiënt $0$ krijgt (dat is de $0$ links van de komma in $0{,}\underline{142857}$) en $1$ zelf als rest  overhoudt. 

In de tabel zie je dat de lengte van de herhalende groep cijfers gelijk is aan de eerste macht van $10$ die rest $1$ geeft bij deling door $7$. De reden is eenvoudig: op dat moment begint de staartdeling als het ware weer opnieuw. En dat kan ook niet anders, want bij delen met rest door $7$ zijn maar $6$ verschillende resten mogelijk, namelijk $1$, $2$, $3$, $4$, $5$ en $6$. 

Ook zie je dat de staartdeling voor $3/7$ op de tweede regel begint, die van $2/7$ een stap later, dan die van $6/7$ enzovoort; en dat verklaart de volgorde in het tweede
tabelletje hierboven. Nu is ook duidelijk waarom je bij $1/3$ periode $1$ krijgt: $10^1 = 3 \times 3 + 1$. 

De periode van $1/11$ is makkelijk te zien: $10^2 = 9 \times 11 + 1$. 

Opgave 1 Hoe zit het bij $13$? Ga maar aan het werk: maak een staartdeling van $1/13$, je zult zien dat $10^6$ rest $1$ heeft bij deling door $13$. Dus de periode is gelijk aan $6$ en de helft van de twaalf getallen $1, 2, \ldots , 12$ heeft hetzelfde cijfergroepje als $1. Welke getallen zijn dat? De andere zes hebben ook een groepje cijfers gemeen. Bepaal dat groepje. Opgave 2 Bij het volgende priemgetal, $17$ krijgen we weer de volle lengte. Werk de staartdeling maar uit en controleer dat het figuur 2 klopt. De decimale recyclingschijf van $17$. Stel, je wilt de decimalen weten van $14/17$. Zoek $14$ op in de buitenring, en lees vanaf daar met de klok mee de decimalen af in de binnenring: $14/17 = 0{,}\underline{823529411764705}$. Opgave 3 Als je het getal $142857$ achtereenvolgens met $1, 2, \ldots , 6$ vermenigvuldigt krijg je alle opgeschoven versies van het eerste getal terug.  Dat lukt ook als je de eerste $16$ cijfers van $1/17$ neemt (wel de nul aan het begin laten staan): door te vermenigvuldigen met $1$ tot en met $16$ draai je de cijfers rond.  Kun je zoiets ook voor andere lengten maken? Bijvoorbeeld een getal van tien cijfers dat door met $1$ tot en met $10$ te vermenigvuldigen rondgedraaid wordt?

Reptend

Ten slotte: de priemgetallen $p$ waarvoor $1/p$ periode $p - 1$ heeft worden 'reptend' genoemd. Er is een hele Wikipedia-pagina over deze priemgetallen en het is nog niet bekend of er oneindig veel van zijn.

Waarom?

Hier wat uitleg van sommige beweringen hierboven. 

Aan de staartdeling kun je zien dat de periode nooit groter dan $N - 1$ kan zijn. Immers in de derde kolom kunnen alleen de getallen 1 tot en met $N - 1$ staan en dat betekent dat onder de eerste $N$ resten een getal twee keer voor moet komen. Tussen die twee getallen zien we de zich herhalende groep cijfers ontstaan. 

Als $p$ een priemgetal is geldt altijd dat $10^p - 1$ een rest van 1 heeft bij deling door $p$; dit volgt uit de Kleine Stelling van Fermat (zoek die maar eens op). Hieruit volgt dat de lengte van de zich herhalende groep cijfers een deler is van $p - 1$ (dat hebben we bij $13$ gezien, de lengte was $6$). 

Waarom wordt de $N - 1$ zeker niet gehaald als $N$ geen priemgetal is? Dan moet je naar de grootste gemene deler van $10$ en $N$ kijken. Die kan $1$, $2$, $5$, of $10$ zijn. De rest van $10^n$ bij deling door $N$ is dan altijd deelbaar door ${\rm ggd}(10, N)$, dus in de laatste drie gevallen is het aantal mogelijke resten nooit meer dan de helft van $N$, en dat betekent dat de lengte van het zich herhalende deel ook niet meer is dan $N/2$. Maar $N/2$ is kleiner dan $N - 1$.

Als ${\rm ggd}(10, N) = 1$ dan geldt ${\rm ggd}(10^n, N) = 1$ voor alle $n$ en voor elke rest $r$ die we tegenkomen geldt ook ${\rm ggd}(r, N) = 1$. Maar als $N = k \times l$ met $k, l < N$ is de rest van $10^n$ bij deling door $N$ nooit een veelvoud van $k$ of $l$ en dat betekent dat zeker $N/l$ getallen niet als rest voorkomen, en $N/l \ge 2$, dus er komen niet meer dan $N - 2$ resten voor.