
De Zoekverhouding: zoeken naar een lijn of naar een Pokémon
Als je iets zoekt en je weet niet waar het is, dan volg je een strategie waarmee je alle mogelijke plekken langsgaat. Iemand die wel weet waar iets is zal er met een kortste pad naartoe gaan. De zoeker zal dus meer moeten lopen. Hoeveel meer, daar gaat dit artikel over.
Het zwemmersprobleem
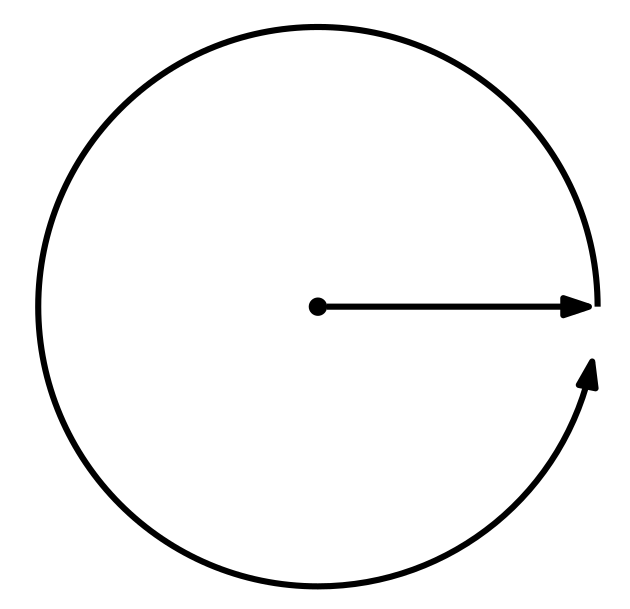
om de waterkant te bereiken
Stel je voor je bent in een groot meer beland, de mist is heel dicht, maar je weet dat je precies $1$ kilometer van de waterkant af bent. De kant is lang en recht, dat weet je ook. Je weet alleen niet in welke richting de kant is. Wel kan je perfect afstanden en richtingen zwemmen. Wat is je strategie om, zelfs als je pech hebt, zo snel mogelijk de kant te bereiken? Je weet pas dat je de kant bereikt hebt als je er echt bent.
Een eerste strategie is om $1$ kilometer in een willekeurige richting te zwemmen, en dan de omtrek van een cirkel met straal $1$ kilometer te zwemmen. Dit is te zien in figuur 1. Je zal dan zeker binnen een afstand van $1+2\pi=7,28...$ de waterkant bereiken. De waterkant is namelijk een lijn die de cirkel raakt, en waar de lijn de cirkel ook raakt, je zal 'm vinden.
Is er een betere strategie? Ja, het is beter om niet de cirkel helemaal rond te zwemmen, maar na driekwart van de cirkel volgens een raaklijn verder te zwemmen. Nu zal je de waterkant vinden na hoogstens $1$ kilometer na het verlaten van de cirkel. Kijk maar naar het linker deel van figuur 2. In totaal zwem je dan $2 + 3\pi/2 = 6,71...$ kilometer.
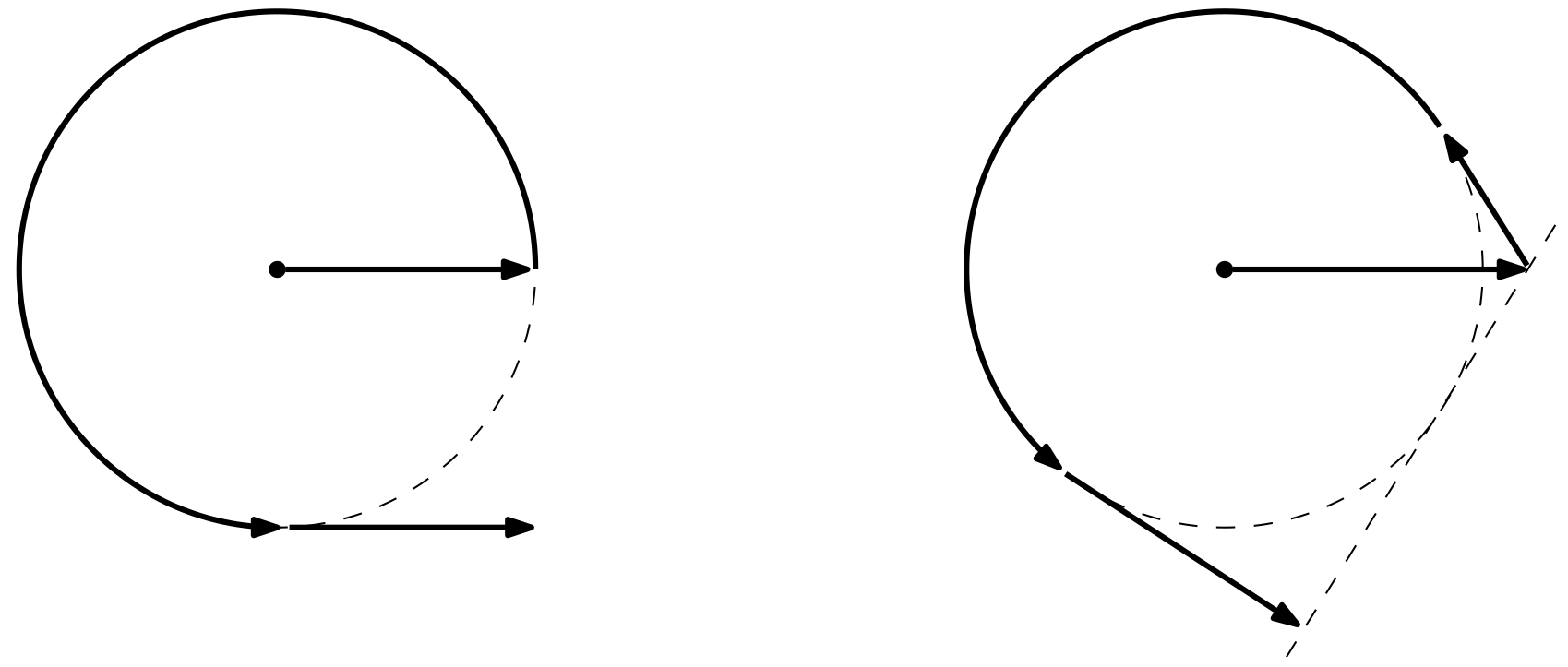
Het kan nog iets beter. Je kan vanaf je beginpunt iets verder dan $1$ kilometer rechtdoor zwemmen, dan volgens een raaklijn terug naar de cirkel, en deze weer volgen voor een stuk totdat je weer langs een raaklijn de cirkel verlaat, in een rechte lijn. Als je weet hoever je doorzwemt, dan kan je de plek waar je de cirkel weer verlaat construeren met een hulplijn die raakt aan de cirkel. Je zwemt namelijk loodrecht op de laatst mogelijke waterkant, de kant die we net niet vonden na het eerste stuk rechtdoor zwemmen. Dit is te zien aan de rechterkant van figuur 2. Nu zwem je slechts $6.39...$ kilometer.
Als je niet $1$ maar $2$ kilometer van de waterkant af was, dan zou je natuurlijk $14,56...$, $13,42...$ of $12,78...$ kilometer zwemmen, afhankelijk van je strategie. De factor die je méér zwemt dan iemand die weet welke kant op de waterkant is, is het interessante getal en hoort bij een strategie. Deze factor heet de zoekverhouding van een strategie: de maximale afstand die je aflegt met je zoekstrategie, gedeeld door de afstand die iemand aflegt die niet hoeft te zoeken.
Zoeken naar een lijn
In 1988 schreven Baeza-Yates, Culberson en Rawlins een technisch rapport over dit soort zoekproblemen. Zij bekeken allerlei situaties waarbij een lijn in het vlak wordt gezocht (later verscheen een kortere versie in een wetenschappelijk tijdschrift). Het probleem van de zwemmer is in feite het probleem van het vinden van een lijn (de rechte waterkant) als je alleen maar weet dat die een bepaalde afstand $1$ van je vandaan is.
Hier is een makkelijker voorbeeld van zo een probleem. We nemen aan dat je zelf een punt in de oorsprong van het vlak bent, je zoekt een lijn, en je weet niet alleen dat de lijn op afstand $1$ van je is, maar zelfs dat de lijn verticaal is.
Opgave 1
Bedenk zelf welke strategie je gebruikt en wat dan de zoekverhouding is.
Hier is een derde versie van dit soort probleem: je zoekt nog steeds een verticale lijn, maar nu weet je niet hoe ver weg die is. Laten we wel aannemen dat je weet dat de lijn minstens op afstand $1$ van je is, maar het kan heel veel meer zijn. Wat is nu je strategie met de kleinste zoekverhouding?
Dit probleem is eigenlijk een $1$-dimensionaal probleem dat ook bekend staat als het zoeken naar een deur in een zeer lange rechte muur. Je weet niet of de deur naar links of naar rechts is, en ook niet hoe ver weg de deur is. In het probleem met de verticale lijnen zal je alleen op de $x$-as lopen, dus de muur is de $x$-as, en de plek waar de verticale lijn de $x$-as snijdt is de deur.

De volgende strategie blijkt optimaal te zijn, dat wil zeggen, deze geeft de kleinst mogelijke zoekverhouding van alle mogelijke strategieën. Ga eerst $1$ naar links, dan terug naar het beginpunt. Vervolgens $2$ naar rechts, en weer terug naat het beginpunt. Dan $4$ naar links, en terug naar het beginpunt. En zo vervolgen we met afstanden $8, 16, 32, 64, \ldots$
afwisselend naar rechts en naar links (en steeds terug naar het beginpunt).
Om de zoekverhouding te bepalen hebben we de volgende reeks nodig:
$$\sum_{i=0}^k 2^i = 1 + 2 + 4 + 8 + \cdots + 2^k = 2^{k+1}-1.$$
Hiermee kunnen we namelijk bepalen hoe ver we hebben gelopen als we zojuist een afstand $2^k$ in een richting en terug zijn gegaan. Dat is $2\cdot (2^{k+1}-1)= 2^{k+2}-2$.
Stel je voor dat we zojuist naar links waren gegaan over een afstand $2^k$, en we de deur nèt niet vonden. De deur staat bijvoorbeeld op afstand $2^k+ 0,001$. Dit is de grootste pech die je kan hebben met deze strategie.
Na het teruggaan vervolgen we dan naar rechts over een afstand $2^{k+1}$, en terug. Dan is ons plan om $2^{k+2}$ naar links te gaan, maar ontdekken de deur op afstand $2^k$ plus een klein beetje. Het is eenvoudig na te gaan dat we nu $9\cdot 2^k$ plus een klein beetje gelopen hebben, terwijl het in $2^k$ plus een klein beetje had gekund. Voor grote waarden van $k$ benadert de verhouding tussen het gelopene en de kortste weg $9$, en dat is de zoekverhouding.
Opgave 2
Ga zelf na dat de zoekverhouding inderdaad $9$ is.
Baeza-Yates en collega's hebben ook aangetoond dat de factor $9$ optimaal is: geen strategie kan een betere constante dan $9$ voor elkaar krijgen.
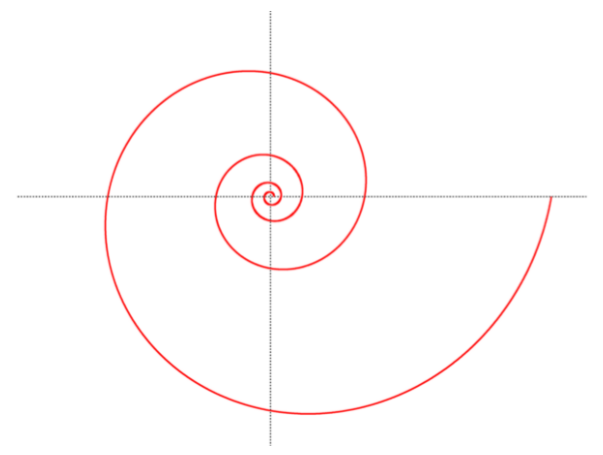
Als meest algemene versie beschouwden Baeza-Yates en collega's de situatie waarbij we niets van de lijn weten: niet hoe ver weg die is en niet welke richting die heeft. Misschien vertelt je intuïtie je wel wat nu een goede strategie is. Inderdaad: het lopen van een bepaalde spiraalvorm. De zoekverhouding die bewezen kan worden voor de logaritmische spiraal is $13,81...$.
Nu kan je je afvragen: hebben alle zoekproblemen een constante zoekverhouding? Het antwoord is nee. Neem het zoeken naar een vakje in een vierkantsraster, waarbij een stap neerkomt op het gaan van een vakje naar één van de vier buurvakjes. We kunnen wel weer een soort spiraal volgen die alle vakjes bezoekt, maar de zoekverhouding zal willekeurig groot worden in de af te leggen afstand. We kunnen ook geen vakje overslaan in onze strategie, want als dat precies het gezochte vakje is, dan vinden we 'm niet.
Als het te zoeken vakje $k$ stappen verwijderd is van het beginpunt (maar de waarde van $k$ weten we niet), dan zullen we proportioneel aan $k^2$ vakjes moeten bezoeken. De zoekverhouding groeit dan proportioneel met $k$, en is dus niet te begrenzen door een constante. Een ander probleem waarvoor geen strategie met constante zoekverhouding bestaat is het zoeken naar een cirkel (bijvoorbeeld met straal $1$).
De kosten van het niet weten
De zoekverhouding van een strategie is dus de verhouding in (loop)kosten tussen iemand die niet weet waar gezocht moet worden en iemand die dat wel weet, in het ergste geval voor degene die het niet weet. De zoekverhouding van een zoekprobleem is de zoekverhouding van de strategie voor dat probleem met de kleinste waarde. Een beetje filosofisch zou je de zoekverhouding "de kosten van het niet weten" kunnen noemen. Iemand die alles weet en iets zoekt zal altijd de kortste weg nemen. Wij willen weten hoeveel erger het voor ons is als we iets niet weten, maar wel een slimme zoekstrategie kiezen.
Pokémon Go
Kort geleden is zoekverhouding-analyse toegepast op het zoeken en vangen van Pokémon in Pokémon Go. Stel je voor je ziet een Pokémon in je NEARBY scherm. Tegenwoordig weet je bij welke PokéStop je moet zoeken, maar in de eerdere versie (en nog steeds als er geen PokéStops in de buurt zijn) wist je niet veel. Meestal speel je Pokémon Go terwijl je aan het lopen bent, en zie je een Pokémon in je SIGHTINGS omdat je binnen z'n bereik bent gekomen. In dat geval weet je op welke afstand je de Pokémon moet vinden, maar niet precies in welke richting. Dit lijkt wel op het zwemmersprobleem! Omdat je een bepaalde kant op liep toen de Pokémon verscheen, weet je dat de Pokémon op een bepaalde half-cirkel moet liggen waarvan jijzelf in het midden staat. Je kan een Pokémon zien en vangen als die dichtbij genoeg is. Kortom, er zijn twee cirkels om je heen, eentje van zo'n $200$ meter voor de waarnemingen (de waarnemingscirckel), en eentje van zo'n $30$ meter voor het vangen (de vangcirkel).
Natuurlijk loop je langs wegen. Die modelleren we met een netwerk. De wegen van het netwerk zijn lijnstukken waarop je alleen vooruit en achteruit kan, en niet zijwaarts. Bij een knooppunt kan je een ander lijnstuk nemen dat bij dat knooppunt begint.
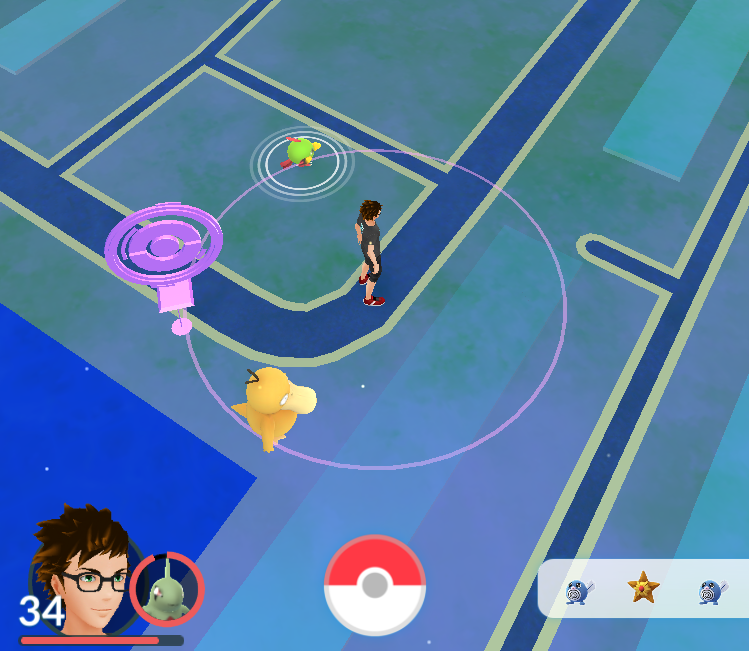
met de vangcirkel om de trainer
We maken nog een paar aannamen om een ideale wereld te maken waarin we dingen kunnen bewijzen. De GPS in onze telefoon is perfect nauwkeurig en geeft altijd meteen door waar we zijn op het netwerk. De Pokémon Go app (zie figuur 5) zal ons meteen vertellen als een nieuwe Pokémon in onze waarnemingscirkel komt en ook als een Pokémon in onze vangcirkel komt (twee Polywags en een Staryu) en ook als een Pokémon in onze vangcirkel komt (Psyduck en Natu). Verder kennen we het netwerk helemaal en weten we alle afstanden.
Als we rondlopen en daardoor komt een Pokémon in de waarnemingscirckel, kunnen we dan de Pokémon in de vangcirkel krijgen zonder veel verder te lopen dan iemand die precies weet waar de Pokémon zit? Welke zoekstrategie moeten we daarvoor gebruiken? Kunnen we de Pokémon vinden met een constante zoekverhouding op elk netwerk, of alleen op bepaalde netwerken?
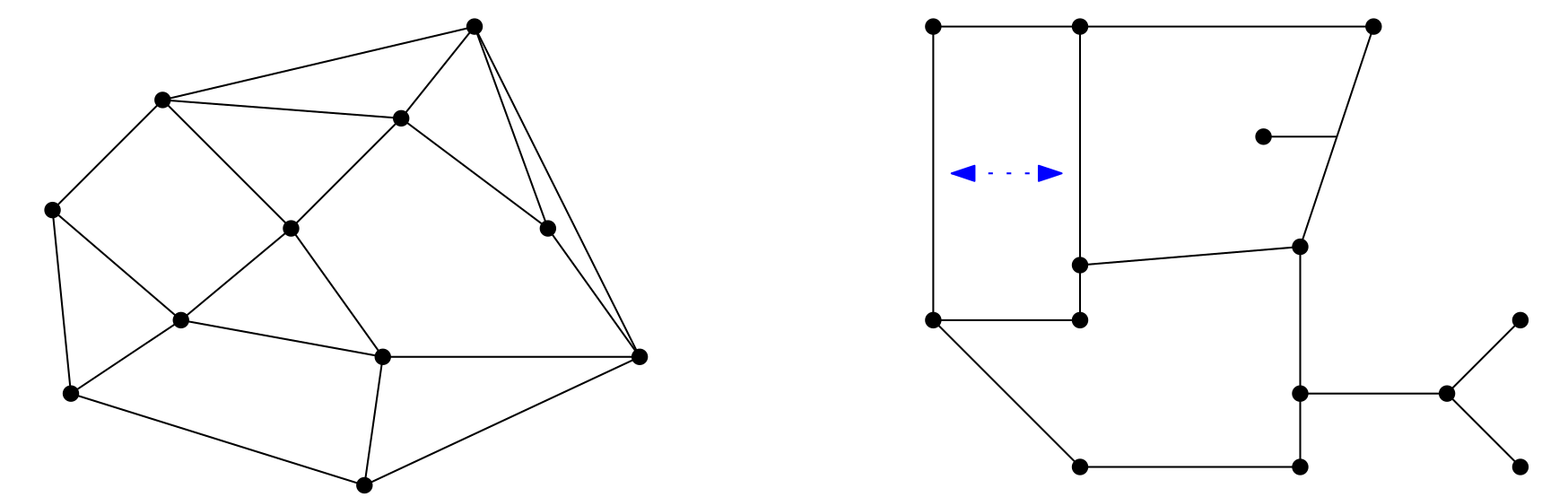
Wat blijkt? Er zijn netwerken te bedenken waarvoor geen zoekstrategie bestaat met een constante zoekverhouding, hoe groot deze constante ook is. Deze netwerken zijn niet bepaald realistisch en lijken dus niet op een stratenpatroon. Maar als het netwerk zo is dat alle omsloten gebieden convex zijn, terwijl de buitenrand van het netwerk ook een convex gebied omsluit, dan is er wel een zoekstrategie waarvoor een constante zoekverhouding bewezen kan worden. Zo'n netwerk is te zien links in figuur 6. De precieze constante hangt af van de verhouding van de straal van de vangcirkel en de straal van de waarnemingscirkel. Ook als het netwerk zelf een constante maximale omwegfactor heeft voor alle twee posities op het netwerk (zie het kader), ook dan bestaat er een strategie met een constante zoekverhouding. Deze constante hangt bovendien af van deze maximale omwegfactor. Een netwerk met omwegfactor $3$ is te zien rechts in figuur 6. De middens van de rechthoek, aangegeven met de blauwe pijl, hebben een omwegfactor $3$, alle andere paren punten hebben een kleinere omwegfactor.
De omwegfactor
De omwegfactor is een eigenschap van een netwerk en is ook een verhouding, namelijk de verhouding tussen de afgelegde weg op het netwerk tussen twee punten en de vogelvluchtafstand tussen deze twee punten. Net zoals bij de zoekverhouding is het de grootste omweg (als vermenigvuldigingsfactor) die de omwegfactor bepaalt. Niet alleen hoekpunten van het netwerk doen mee, ook punten op kanten daartussenin tellen mee.
Laten we als voorbeeld een netwerk nemen dat precies een vierkant van $1$ bij $1$ is. Twee aangrenzende hoeken hebben een afstand over het netwerk die gelijk is aan de afstand voor een vogel, dus hun omwegfactor is $1$. Twee diagonaal overstaande hoeken hebben een afstand over het netwerk van $2$, terwijl een vogel $\sqrt{2}$ moet vliegen. De omwegfactor voor deze twee punten is dus $2/\sqrt{2}=\sqrt{2}$. De twee punten met de grootste omwegfactor zijn de middens van tegenoverliggende zijden. Hier is de afstand over het netwerk $2$, terwijl een vogel maar $1$ hoeft te vliegen.
Opgave 3
Ga nu zelf na dat:
- een gelijkzijdige driehoek een omwegfactor $2$ heeft;
- een cirkel een omwegfactor $\pi/2$ heeft;
- een vierkantsraster een omwegfactor $2$ heeft, voor een $m\times n$ raster.
