Wiskundigen zijn altijd op zoek naar nieuwe oplossingen voor ingewikkelde problemen. Door "out of the box" te denken kunnen er zo elegante methodes gevonden worden. Toen ik op onderzoek uit ging voor mijn profielwerkstuk stuitte ik op het werk van Margherita Piazza Beloch over het oplossen van derdegraads vergelijkingen met origami, en mijn nieuwsgierigheid was direct gewekt. Hoe kan origami, een kunstvorm, nou helpen om wiskundige problemen op te lossen? De ontdekkingsreis die volgde begon bij de basis van de origami-wiskunde.

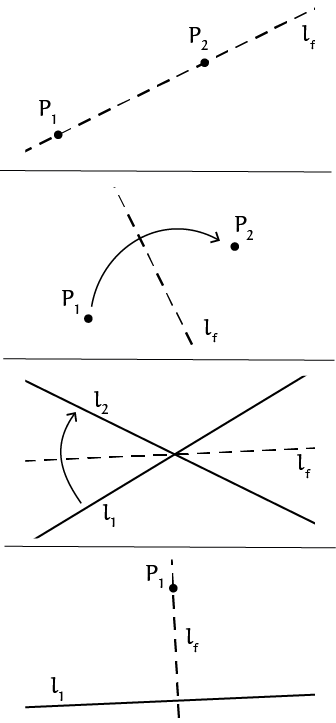
Om wiskundig te gaan vouwen moeten eerst een stel basisregels of axioma's wordenopgesteld. Deze zes origami-axioma's beschrijven de wiskundig gezien verschillende vouwen die met origami mogelijk zijn. De eerste vier (zie ook figuur 1) luiden als volgt:

1. Er bestaat voor twee gegeven punten $P_1$ en $P_2$ één unieke vouwlijn waar $P_1$ en $P_2$ op liggen.
2. Er bestaat voor twee gegeven punten $P_1$ en $P_2$ één unieke vouwlijn die $P_1$ op $P_2$ plaatst.
3. Er bestaat voor twee gegeven lijnen $l_1$ en $l_2$ één unieke vouwlijn die $l_1$ op $l_2$ plaatst.
4. Er bestaat voor een gegeven lijn $l_1$ en een gegeven punt $P_1$ één unieke vouw door $P_1$, die loodrecht op $l_1$ staat.

Deze eerste vier axioma's zijn redelijk vanzelfsprekend. Ze beschrijven een lijn, een middelloodlijn, een bissectrice en een loodlijn. Het vijfde en zesde axioma zijn echter interessanter voor het oplossen van derdegraads vergelijkingen met origami. 

5. Voor gegeven punten $P_1$ en $P_2$ en gegeven lijn $l_1$ bestaan er $0$, $1$ of $2$ vouwen door $P_2$ die $P_1$ op $l_1$ plaatsen.

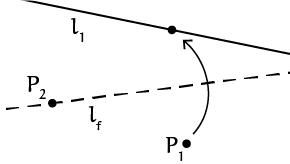
De vouwlijn die door dit axioma wordt bedoeld, is de raaklijn door $P_2$ aan de conflictlijn van $P_1$ en $l_1$. De conflictlijn van $P_1$ en $l_1$ is een parabool, dus de vouwlijn is een raaklijn aan een parabool. Een simpele manier om dit in te zien is door een stip en een lijn op een papier te tekenen. Vouw nu op verschillende manieren de stip naar de lijn toe. Door dit vaak genoeg te doen, wordt uiteindelijk een parabool zichtbaar. Alle vouwen zijn namelijk raaklijnen aan de parabool, zie figuur 3.

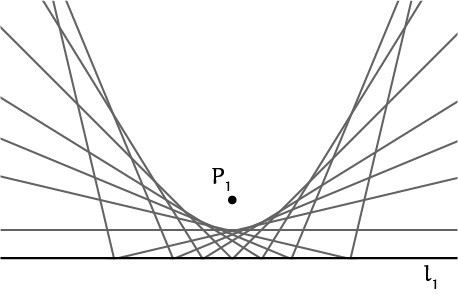
Hier wordt dan ook de connectie tussen origami en polynomen zichtbaar. Als je het snijpunt wilt berekenen van een parabool en een (niet-verticale) lijn, krijg je namelijk te maken met de volgende situatie:

$p: y = a_1x^2 + b_1x + c_1$ en $l: y = b_2x + c_2$.

Voor het snijpunt van $p$ en $l$ betekent dat:

$a_1x^2 + b_1x + c_1 = b_2x + c_2$
$a_1x^2 + (b_1 - b_2)x + (c_1 - c_2) = 0$.

Dit is een tweedegraads vergelijking. Een raaklijn aan een parabool construeren komt dus overeen met het oplossen van een tweedegraads vergelijking.

6. Gegeven twee punten $P_1$, $P_2$ en twee lijnen $l_1$, $l_2$, kunnen we, als deze bestaat, een lijn vouwen zo dat $P_1$ op $l_1$ en $P_2$ op $l_2$ terechtkomt.

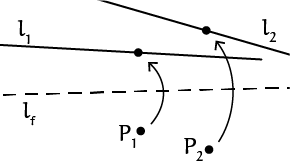
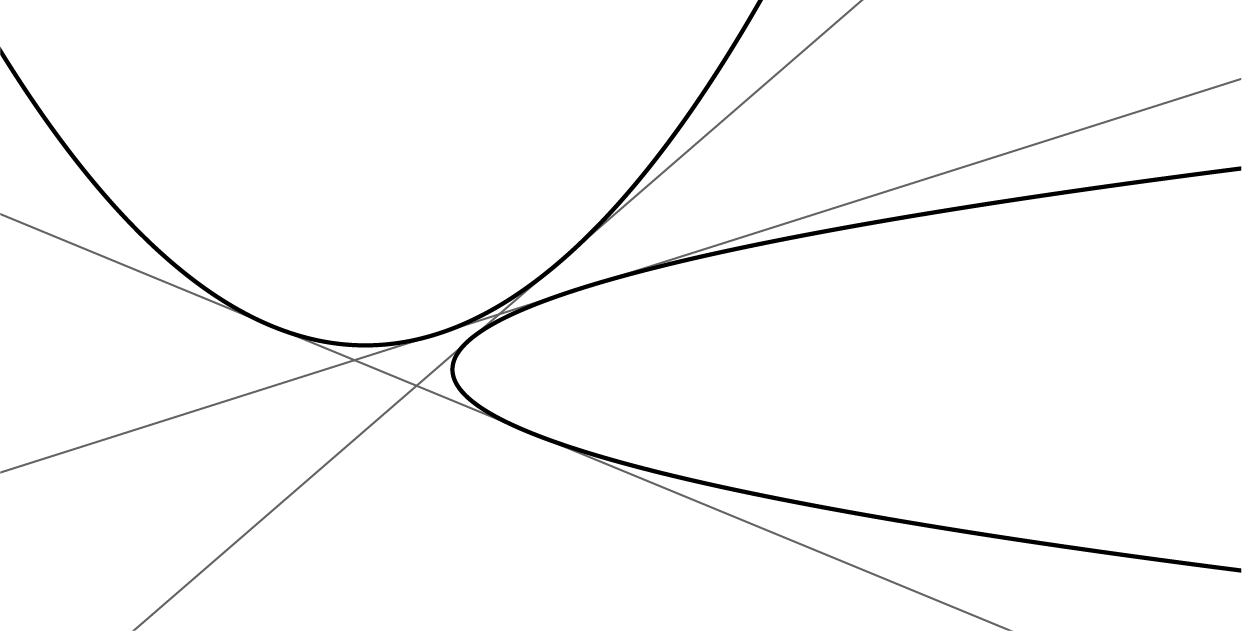
Dit zesde axioma beschrijft het vinden van een gezamenlijke raaklijn aan twee parabolen, aangezien het vouwen van een punt naar een lijn equivalent is aan het vinden van een raaklijn aan een parabool (axioma 5). Door twee parabolen te tekenen en gezamenlijke raaklijnen te zoeken wordt al snel duidelijk dat twee parabolen maximaal drie gezamenlijke raaklijnen hebben (figuur 5). Dit suggereert dat we te maken hebben met een derdegraads vergelijking.

De ontdekster van dit axioma, Margherita Piazza Beloch, legde aan de hand van een constructieprobleem en het werk van Eduard Lill verder uit hoe deze vouwlijn gebruikt kan worden om derdegraads vergelijkingen op te lossen. Het constructieprobleem, waarvan het resultaat bekend staat als Belochs vierkant, is als volgt geformuleerd:

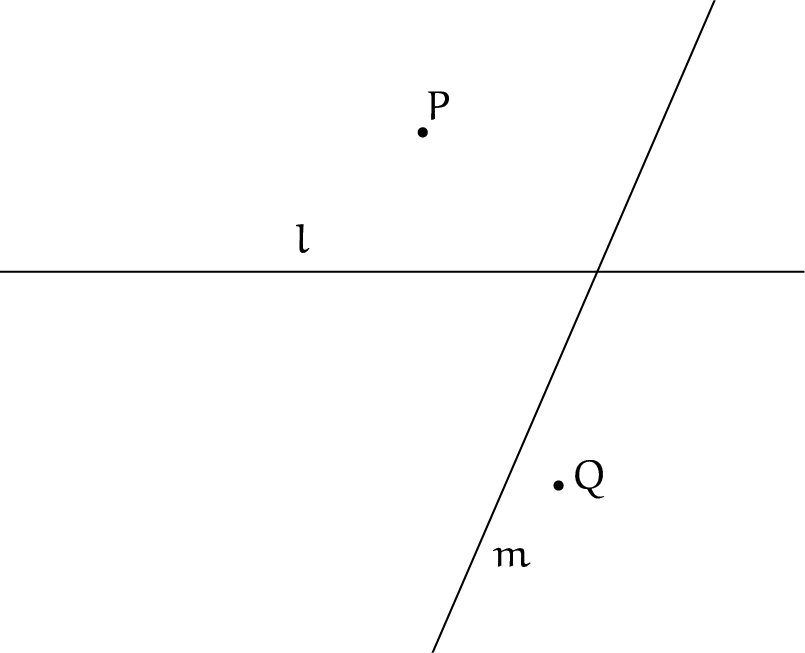
Gegeven lijnen $l$ en $m$ en punten $P$ en $Q$. Construeer een vierkant $WXYZ$ zo dat $X$ en $Y$ respectievelijk op $l$ en $m$ liggen, en dat de zijdes, of het verlengde ervan, respectievelijk door $P$ en $Q$ gaan.

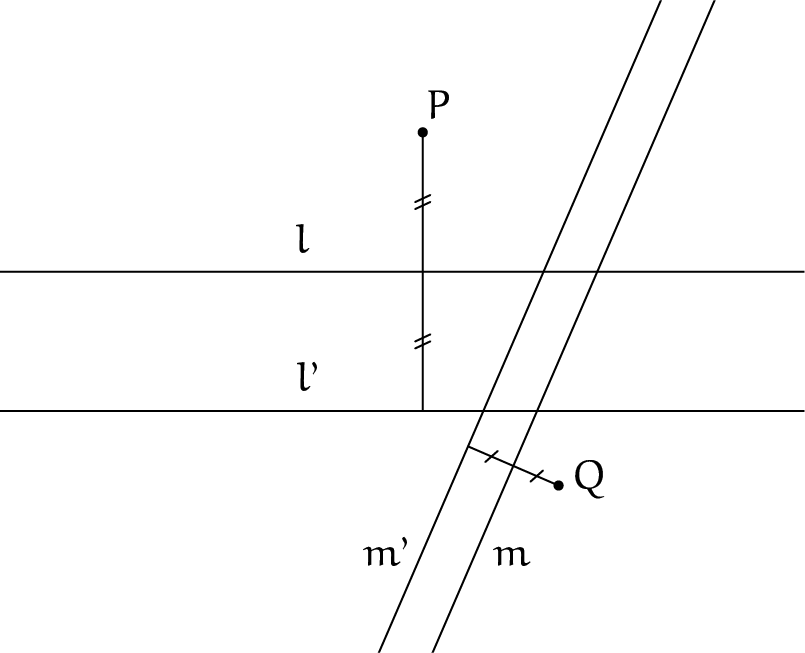
Dit constructieprobleem is volledig op te lossen met behulp van origami. Met behulp van origami-axioma's 1 en 4 kunnen als eerste de lijnen $l'$ en $m'$ gevouwen worden, zodat $d(l', l) = d(l, P)$ en evenzo $d(m', m) = d(m, Q)$. Zie ook figuur 6a en 6b.

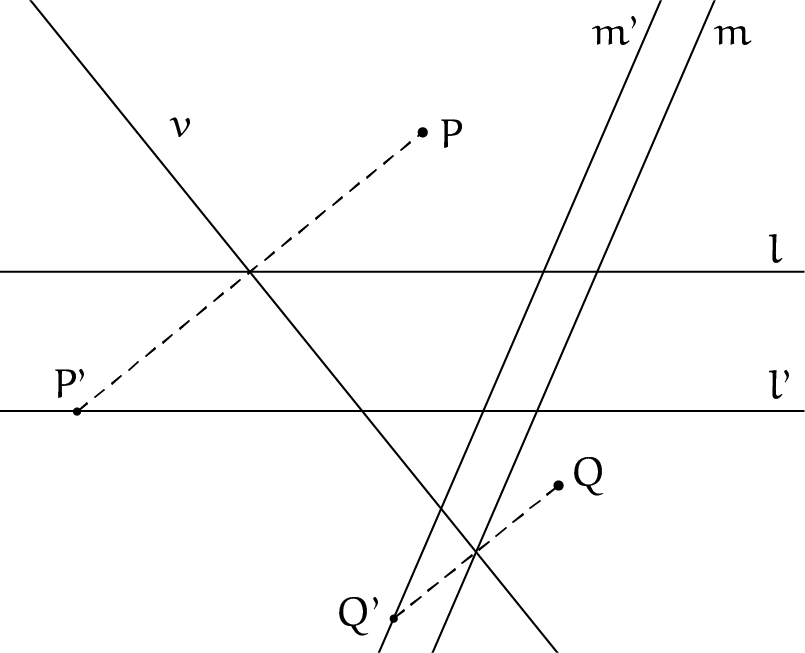
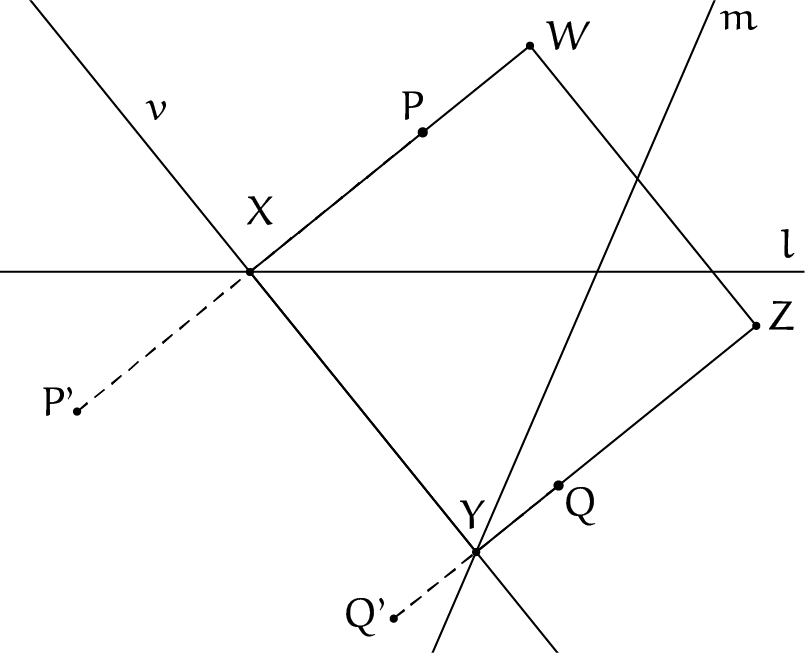
Nu maken we de vouw van Beloch uit axioma 6. Creëer een vouw die $P$ op $l'$ plaatst en $Q$ op $m'$. Noem de plaatsen waar de vouwlijn $v$ door $l$ en $m$ gaat respectievelijk $X$ en $Y$. De eerste zijde van het vierkant is nu gevonden. Door middel van axioma 3 kan ook de rest van het vierkant getekend worden met behulp van de diagonaal (zie figuur 7a en 7b).

Om de rest van Belochs origami-methode te begrijpen is wat voorkennis van het werk van Eduard Lill vereist. Hij ontwikkelde een methode om de nulpunten van polynomen te vinden. In Pythagoras 62-5 werd dit uitgelegd aan de hand van een watergevecht. De eerste stap van deze methode is om het pad van een vergelijking te tekenen, bijvoorbeeld een derdegraads vergelijking $a_3x^3 + a_2x^2 + a_1x + a_0 = 0$. Dat gaat op de volgende manier: 

1. Teken een lijnstuk met als lengte de coëfficiënt voor de hoogste macht van het polynoom, van links naar rechts.
2. Draai $90^{\rm o}$ tegen de klok in en teken een lijnstuk met als lengte de coëfficiënt voor de macht van $x$ die 1 lager is. Teken lijnstukken met een negatieve coëfficiënt precies de andere kant op, oftewel achteruit. Dit heeft geen invloed op de volgende draairichting. Als een macht niet voorkomt wordt er geen lijnstuk getekend, maar wel gedraaid. De richtingen van de lijnstukken zijn dan als volgt (begin dus bij a_3, de coëfficiënt van de hoogste macht):
   
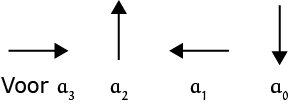
3. Herhaal stap 2 tot alle machten (ook de nulde) zijn afgegaan.

Een verdere uitleg van de watergevechtmethode staat in Pythagoras 62-5. Voor de origami-methode hebben we genoeg aan het pad van de vergelijking. In dit geval wordt er niet met waterstralen geschoten, maar wordt er een papier gevouwen. Hier zijn nog twee hulplijnen voor nodig. De eerste lijn $l$ wordt zo getekend dat deze loodrecht staat op het verlengde van het eerste lijnstuk ($AB$ in figuur 8) en dat de afstand tot het beginpunt van het pad van de vergelijking tweemaal dit lijnstuk is (dus $2AB$). De lijn $m$ wordt op een vergelijkbare manier getekend. Lijn $m$ staat loodrecht op het verlengde van het laatste lijnstuk $DE$, zodanig dat de afstand tot het eindpunt van het pad van de vergelijking $2DE$ is.

Voorbeeld

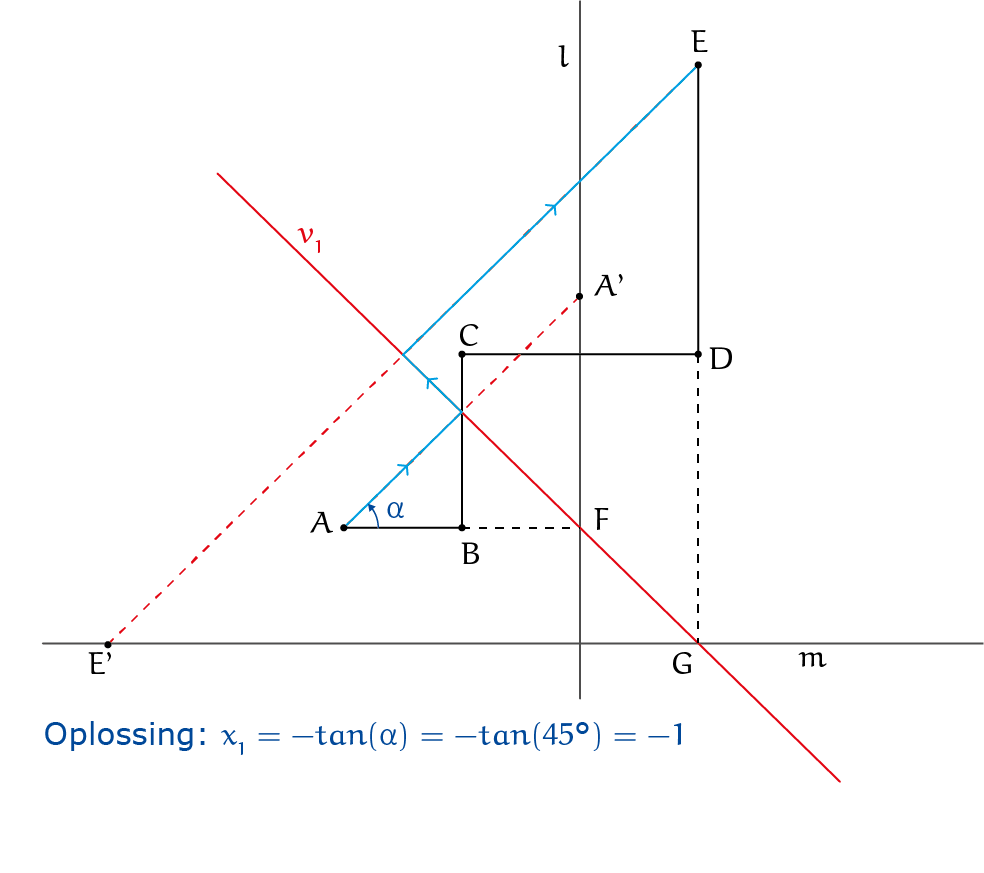
Laten we de origami-methode bekijken aan de hand van het voorbeeld $2x^3 + 3x^2 - 4x - 5 = 0$. Het pad is getekend in figuur 8, evenals de lijnen $l$ en $m$. $F$ ligt op lijn $l$ zodat $AB = BF$ en $G$ ligt op lijn $m$ zodat $ED = DG$.

Met behulp van deze lijnen wordt er nu gevouwen. Het doel is om met één vouw zowel beginpunt $A$ op lijn $l$ te plaatsen als eindpunt $E$ op lijn $m$. De gezochte vouw is de vouw van Beloch die ook in het constructieprobleem voor het vierkant werd gebruikt. De rode lijn in figuur 8 is de vouwlijn die gezocht wordt voor de vergelijking $2x^3 + 3x^2 - 4x - 5 = 0$. De plaatsen waar $A$ en $E$ landen op de lijnen worden aangegeven met respectievelijk $A'$ en $E'$. Dan kunnen nu de nulpunten van de polynoom gevonden worden met behulp van de hoek $\alpha$ tussen $AB$ en $AA'$ en de formule $x = -tan(\alpha)$. Voor het voorbeeld is de grootte van de aangegeven hoek $\alpha = 45^{\rm o}$. Invullen in de formule geeft $x = -\tan(45^{\rm o}) = -1$. Invullen in de vergelijking $2x^3 + 3x^2 - 4x - 5 = 0$ laat zien dat deze $x$ inderdaad een oplossing is. Ter vergelijking zijn in blauw ook de waterstralen getekend.

Derdegraads vergelijkingen kunnen meerdere reële oplossingen hebben. In dat geval zijn er ook meerdere vouwen mogelijk die zowel beginpunt $A$ op lijn $l$ plaatsen als eindpunt $E$ op lijn $M$. De twee andere oplossingen staan in figuur 9.

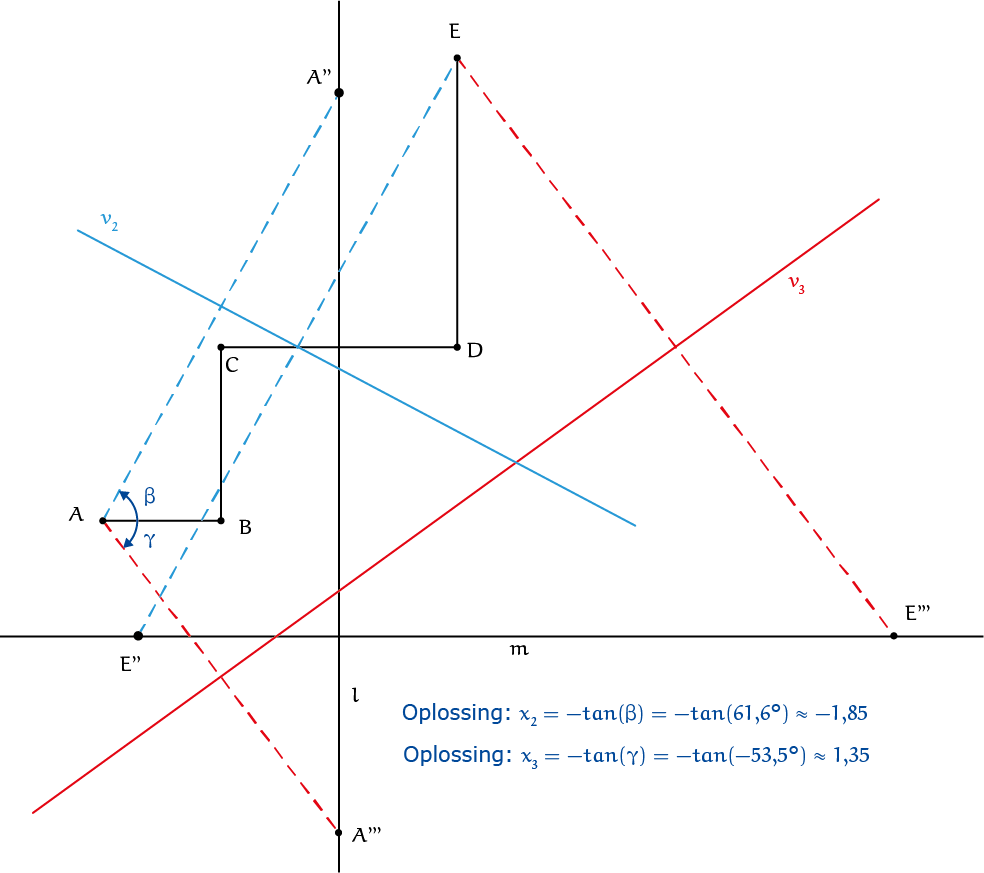
Deze methode is gelijk aan het vinden van Belochs vierkant. Er wordt namelijk een "vierkant" $WXYZ$ geconstrueerd zo dat $X$ en $Y$ respectievelijk op de lijnen door $BC$ en $CD$ liggen. De zijde $XY$ is precies het deel van de vouw dat wordt gebruikt voor de waterstraal in figuur 8. In figuur 10, met vergelijking $3x^3 - 2x^2 + 4x - 5 = 0$, zijn de constructielijnen $l$ en $m$ niet getekend en de punten $A'$ en $E'$ ook niet, Wel is daarin het segment $XY$ van de vouwlijn v te zien. De zijdes van het vierkant (of het verlengde daarvan) gaan door het begin- en eindpunt van het pad van de vergelijking. Enkel de hoekpunten $W$ en $Z$ moeten nog geplaatst worden.

De origami-methode is in feite slechts een alternatief voor Lills methode, omdat het middelste gedeelte van de "waterstraal" uit Pythagoras 62-5 op de vouwlijn in de origami- methode ligt. Deze alternatieve oplosmethode werkt enkel voor derdegraads polynomen, in tegenstelling tot Lills "waterstraal"-methode. Toch laat deze methode weer zien hoe verrassend wiskunde kan zijn: origami biedt meer constructiemogelijkheden dan passer en liniaal, waarmee derdegraads vergelijkingen immers niet opgelost kunnen worden.

		Heb jij een profielwerkstuk gemaakt over wiskunde? Stuur het werkstuk dan op naar de redactie van Pythagoras! Pythagoras looft drie prijzen uit voor de beste wiskundeprofielwerkstukken van dit schooljaar. De prijzen zijn 250, 125 en 75 euro en bij voldoende kwaliteit een artikel zoals hierboven in Pythagoras. De wedstrijd is als volgt georganiseerd: universitaire wiskundigen uit verschillende vakgebieden selecteren maximaal drie profielwerkstukken. De auteurs van deze profielwerkstukken houden een presentatie van tien minuten op het Nederlands Mathematisch Congres 2024, dat op woensdagmiddag 3 april in De Werelt in Lunteren zal plaatsvinden. De eerste, tweede en derde prijs worden daar door middel van een stemming onder jury en het publiek bepaald. Er is altijd veel belangstelling voor het eindresultaat, dus wij plaatsen de profielwerkstukken in elk geval op onze website (deelname = toestemming). We ontvangen profielwerkstukken graag in pdf. Zorg dat je het werkstuk (inclusief naam, adres en school) stuurt naar [email protected]. Je inzending moet uiterlijk 1 maart 2024 bij ons binnen zijn.