Op een plein staat een minidraaimolen: één waarin drie kinderen kunnen plaatsnemen. De draaimolen staat op een cirkelvormige ondergrond die verdeeld is in drie sectoren. Elke sector heeft een eigen (unieke) kleur. Bovendien draagt elk kind een petje. De kleuren van de petjes zijn precies hetzelfde als de kleuren van de sectoren.

Als de draaimolen ronddraait, passeert elk kind de gekleurde sectoren op de ondergrond. Kunnen de kinderen zó in de draaimolen gaan zitten, dat bij elke stand van de draaimolen er precies één kind een petje heeft met dezelfde kleur als zijn ondergrond? Met een ‘stand van de draaimolen’ bedoelen we een situatie waarbij elk kind zich geheel binnen één sector bevindt, dus niet half op de ene sector en half op een andere.

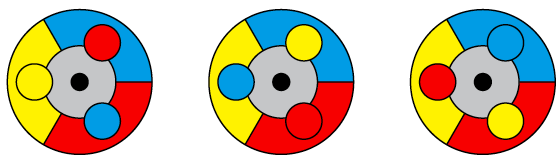
Figuur 1 laat zien dat dit inderdaad mogelijk is. En hoe zit het bij grotere draaimolens? Stel dat er plek is voor vijf kinderen, en dat de ondergrond verdeeld is in vijf sectoren, in vijf verschillende kleuren. Kunnen de kinderen met hun petjes dan zó plaatsnemen dat er weer precies één kind is met een petje in dezelfde kleur als zijn ondergrond? Jazeker, zie figuur 2.

Algemeen

We hebben een draaimolen met vier plekken (en vier kleuren) overgeslagen. Misschien wil je eerst zelf proberen de vier kinderen volgens onze spelregel in de draaimolen te plaatsen, voordat je verder leest.

Kunnen we ook iets algemeens zeggen over dit draaimolenprobleem? Stel, er is op de draaimolen plaats voor n kinderen, en de ondergrond bestaat uit n sectoren, in n verschillende kleuren.

Hoe construeer je een kleuring voor een draaischijf met n sectoren, zodanig dat bij elke keer draaien de kleur van precies één petje samenvalt met de kleur van de ondergrond?

Om te beginnen vervangen we de kleuren door de getallen 1 tot en met n. We maken een tabel. Boven zetten we de kleuren van de ondergrond (genummerd 1, 2, 3, ..., n) en daaronder in n rijen de n mogelijke draaiingen, waarbij de kleuren van overeenkomstige petjes (met ondergrondkleuren) zijn onderstreept.

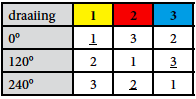
Voor n = 3 krijgen we:

En voor n = 5:

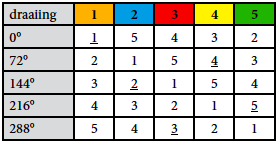
Nummer de n rijen nu van 0 tot en met n – 1. Trek van elk onderstreept getal het nummer van zijn rij af. Voor n = 3 krijgen we dus: 1 – 0 = 1, 3 – 1 = 2 en 2 – 2 = 0. Als een verschil 0 is of negatief, tellen we er n bij op; hier veranderen we dus 2 – 2 = 0 in 2 – 2 + 3 = 3.

Voor n = 5 krijgen we achtereenvolgens 1 – 0 = 1, 4 – 1 = 3, 2 – 2 = 0, 5 – 3 = 2 en 3 – 4 = –1. Na aanpassing krijgen we 1 – 0 = 1, 4 – 1 = 3, 2 – 2 + 5 = 0 + 5 = 5, 5 – 3 = 2 en 3 – 4 + 5 = –1 + 5 = 4.

In beide gevallen krijgen we als resultaat de positie van k in rij nummer 0. Dat krijgen we ook in het algemeen: als k in rij i onderstreept is, staat hij op positie k en dat is i posities naar rechts vergeleken met rij 0. Maar i aftrekken betekent i stappen naar links doen, dus k – i wijst naar de positie van k in rij 0, tenzij er 0 of minder uit k – i komt: dan wijst k – i + n naar de juiste plek op de draaimolen.

Hieruit volgt dat de aangepaste verschillen precies de getallen 1 tot en met n opleveren.

Als we alle verschillen bij elkaar optellen, krijgen we

$$1 + 2 + 3 + ... + n – (0 + 1 + 2 + ... + (n – 1)) = n.$$

Als we de aangepaste verschillen bij elkaar optellen, krijgen we de som van alle getallen 1 tot en met n:

$$1 + 2 + 3 + ... + n = \frac{1}{2} n(n + 1).$$

De aanpassing komt neer op een aantal malen n optellen; dus de twee sommen verschillen een n-voud en dus moet $\frac{1}{2} n(n + 1) – n = \frac{1}{2} (n – 1)n$ deelbaar zijn door n. Dit is alleen het geval als n – 1 deelbaar is door 2, dus als n oneven is.

Conclusie: áls er een oplossing is, dan is n oneven. En dat betekent: als n even is, is er geen oplossing! In het bijzonder is het probleem dus niet oplosbaar voor een draaimolen met vier plaatsen.

De spannende vraag is nu hoeveel oplossingen er zijn als n oneven is. Hoe dat in z’n werk gaat is een stuk lastiger. Wie er meer over wil weten, kan kijken in de Online Encyclopedia of Integer Sequences (OEIS), rij A006717.