De beroemde wiskundige Euler vroeg zich af of je iets soortgelijks ook voor derdemachten en hoger zou kunnen doen. Hij vroeg zich af of er gehele getallen te vinden zijn, zodat bijvoorbeeld $a^3 + b^3 + c^3 = d^3$ of $a^4 + b^4 + c^4 + d^4 = e^4$. Die blijken er inderdaad te zijn. 

De Griekse wijsgeer Plato wist al dat $3^3 + 4^3 + 5^3 = 6^3$. Daarom wordt $6^3 = 216$ een getal van Plato genoemd. Voor de derdemacht zijn er meer oplossingen, zoals bijvoorbeeld $1^3 + 6^3 + 8^3 = 9^3$ of $7^3 + 14^3 + 17^3 = 20^3$. En ook voor de vierdemacht kun je oplossingen maken, zoals $30^4 + 120^4 + 272^4 + 315^4 = 353^4$. 

Als we veronderstellen dat alle getallen verschillend zijn van nul, dan moet je altijd ten minste drie derdemachten bij elkaar op tellen om een andere derdemacht te krijgen. Er zijn heel veel oplossingen voor $a^3 + b^3 + c^3 = d^3$, maar er zijn er geen voor $a^3 + b^3 = c^3$. Dat laatste is een speciaal geval van de beroemde Laatste Stelling van Fermat, geformuleerd in 1637 en pas bewezen in 1995, die zegt dat $a^n + b^n = c^n$ nooit positieve gehele oplossingen heeft voor $n \ge 3$. 

Euler vermoedde in 1769 dat je voor een gelijkheid met vierdemachten ook altijd ten minste vier vierdemachten op zou moeten tellen. Maar hij zat ernaast. In 1986 liet de Amerikaanse wiskundige Noam Elkies zien dat (houd je vast): 

$$2.682.440^4 + 15.365.639^4 + 18.796.760^4 = 20.615.673^4.$$ 

Links en rechts komt er $180.630.077.292.169.281.088.848.499.041$. 

Negatieve getallen 

Bij kwadraten maakt het niet uit of je $6^2$ uitrekent of $(-6)^2$. In beide gevallen komt er $36$ uit. Maar bij derdemachten is $6^3 = 216$, terwijl $(-6)^3 = -216$. Het maakt dus uit of je een positief of een negatief getal tot de derde macht doet. We kunnen eens kijken of de gelijkheid $a^3 + b^3 + c^3 = d^3$ meer oplossingen heeft als $a$, $b$, $c$ of $d$ ook negatief mag zijn. Dat blijkt zo te zijn. Bijvoorbeeld $(-1)^3 + 9^3 + 10^3 = 12^3$ of $(-2)^3 + 9^3 + 15^3 = 16^3$. 

Opgave

Uit dit voorbeeld volgt dat alvast $9^3$ op minstens twee manieren te schrijven is als een som van $3$ derdemachten, namelijk $9^3 = 1^3 + (-10)^3 + 12^3 = 2^3 + (-15)^3 + 16^3$. Denk je dat er ook kwadraten te vinden zijn die op twee verschillende manieren te schrijven zijn als som van twee kwadraten? 

Er zijn dan zelfs zo veel extra manieren dat mensen zich zijn gaan afvragen of je elk getal zou kunnen schrijven als de som van drie (mogelijk negatieve) derdemachten. We kijken dus niet alleen of $a^3 + b^3 + c^3$ bij elkaar een derdemacht vormen, maar of we elk getal kunnen schrijven als een som van drie derdemachten. 

De Britse wiskundige Louis Mordell schreef in 1953: “Ik weet helemaal niets over de gehele oplossingen van de vergelijking $a^3 + b^3 + c^3 = 3$ behalve dan dat $(1, 1, 1)$ en $(4, 4, -5)$ allebei voldoen; en het moet heel moeilijk zijn om iets te weten te komen over andere oplossingen. Men kan zich afvragen of het probleem van het vinden van andere oplossingen vergelijkbaar is met het bepalen van de plaats van een welbepaalde opeenvolging van cijfers zoals bijv. $123456789$ in de decimale ontwikkeling van het getal $r$.” Daarmee begon een speurtocht naar getallen die te schrijven waren als som van drie derdemachten. Men wilde weten welke getallen allemaal te schrijven waren als $a^3 + b^3 + c^3$ met $a$, $b$ en $c$ gehele getallen die ook negatief mogen zijn. En dat bleek niet mee te vallen! 

Waarom zit een derdemacht hooguiteentje naast een negenvoud? 

Als je de rij van de gehele getallen opschrijft, dan zie je dat elk getal hooguit eentje verschilt van een drievoud. Ieder geheel getal kun je dus schrijven als $3i + j$, waarbij $j = -1$, $j = 0$ of $j = 1$.

Je kunt $3i + j$ tot de derde macht doen en dan haakjes wegwerken: 

$$(3i + j)^3 = (3i + j) \cdot (3i + j)^2 = \\
(3i + j) \cdot (9i^2 + 6i\cdot j + j^2) = \\
27i^3 + 27i\cdot j^2 + 9i^2\cdot j + j^3$$

Het valt gelijk op dat de eerste drie termen allemaal negenvouden zijn. Je kunt het dus schrijven als: 

$$(3i + j)^3 = 9n + j^3  \mbox{met}\\ 
n = 3i^3 + 3i^2\cdot j + i\cdot j^2$$

Omdat $ j^3$ altijd $-1, 0$ of $1$ is, zal een derdemacht hooguit één afwijken van een negenvoud. 

Niet alle getallen zijn mogelijk 

Gelukkig kun je vrij gemakkelijk zien welke getallen in elk geval niet te schrijven zijn als som van drie derdemachten. Daarvoor moet je eerst weten dat een derdemacht altijd een veelvoud van negen is of juist eentje meer of minder dan een negenvoud. 

In het kader staat uitgelegd waarom. Een derdemacht is dus altijd te schrijven als $9n - 1$, $9n$ of $9n + 1$ voor een bepaalde gehele waarde van $n$. Bijvoorbeeld: 

$6^3$	$=$	$24\cdot 9$
$11^3$	$=$	$148\cdot 9 - 1$
$13^3$	$=$	$244\cdot 9 + 1$

Als je nu drie willekeurig derdemachten bij elkaar optelt, kun je dus nooit uitkomen op $9n - 4$ of $9n + 4$. Probeer het maar eens. 

Omdat je maar drie derdemachten hebt, kom je niet verder dan $9n + 3$. (Je kunt wel uitkomen op bijvoorbeeld $9n + 6$, omdat dit hetzelfde is als een $9n - 3$ met $n$ eentje hoger.) 

Opgave

Ga na dat een kwadraat altijd ofwel een viervoud is, ofwel eentje meer dan een viervoud. 

Drie derdemachten zijn opgeteld dus nooit een negenvoud plus vier of een negenvoud min vier. Maar kan het wel voor alle andere getallen? Oftewel: kun je voor elk getal $k$ altijd drie gehele (mogelijk negatieve) getallen 
$a$, $b$ en $c$ vinden zodat $a^3 + b^3 + c^3 = k$? 

De speurtocht begon (met een beetje hulp van de computer) en leidde al snel tot een rijtje resultaten: 

$1$	=	$0^3 + 0^3 + 13$
$2$	=	$0^3 + 1^3 + 1^3$
$3$	=	$1^3 + 1^3 + 1^3$
$4$		kan niet
$5$		kan niet
$6$	=	$(-1)^3 + (-1)^3 + 2^3$
$7$	=	$0^3 + (-1)^3 + 2^3$
$8$	=	$0^3 + 0^3 + 2^3$
$9$	=	$0^3 + 1^3 + 2^3$
$10$	=	$1^3 + 1^3 + 2^3$
$11$	=	$(-2)^3 + (-2)^3 + 3^3$
$12$	=	$7^3 + 10^3 + (-11)^3$
$13$		kan niet
$14$		kan niet
$15$	=	$(-1)^3 + 2^3 + 2^3$
$16$	=	$(-511)^3 + (-1609)^3 + 1626^3$

De ellendige 33, 42 en 74 

Je ziet dat het laatste resultaat, voor het getal $16$, al aardig uit de hand begint te lopen. Er zijn grote derdemachten nodig om de som nog kloppend te maken. En dat bleek nog maar het begin. In eerste instantie gingen de wiskundigen op zoek naar een manier om de getallen onder de 100 te schrijven als som van drie derdemachten. De laatste loodjes waren het lastigst. 

In 1992 werd gevonden dat 
$$134.476^3 + 117.367^3 + (-159.380)^3 = 39.$$

In 1995 werd gevonden dat

$$4.381.159^3 + 435.203.083^3 + (-435.203.231)^3 = 75.$$

En in 1999 werd gevonden dat

$$(-61.922.712.865)^3 + 60.702.901.317^3 + 23.961.292.454^3 = 52.$$

Vanaf toen bleef het stil. Voor alle getallen onder de $100$ waren sommen van drie derdemachten gevonden (of was er geen oplossing), maar voor de getallen $33$, $42$ en $74$ bleef een oplossing uit. Dat duurde tot 2016. Toen kwam de Nederlander Sander Huisman met: 

$$(-284.650.292.555.885)^3 + 66.229.832.190.556^3 + 283.450.105.697.727^3 = 74.$$

Pas heel recent werd het volgende getal onder de $100$ gevonden. De Britse wiskundige Andrew Booker publiceerde in het voorjaar van 2019 een som van drie derdemachten waar precies $33$ uit kwam en afgelopen september kwam hij met het getal $42$. Er is zelfs een T-shirt te koop met de ontbinding van $42$ als som van drie derdemachten: 

$$(-80.538.738.812.075.974)^3 + 80.435.758.145.817.515^3 + 12.602.123.297.335.631^3 = 42 $$

(zie t.co/cluf9sIEGX). En daarmee waren alle getallen gevonden. Nou ja, in elk geval de getallen tot en met $100$. De meeste dus nog niet... 

Nog meer over het getal 3? 

Weet je nog hoe de speurtocht begon? Met Louis Mordell die maar twee manieren wist om $3$ te schrijven als de som van drie derdemachten: $1^3 + 1^3 + 1^3$ en $4^3 + 4^3 + (-5)^3$. 

Op 16 september 2019 schreef Mark McAndrew, uit het team van Booker op Twitter: 

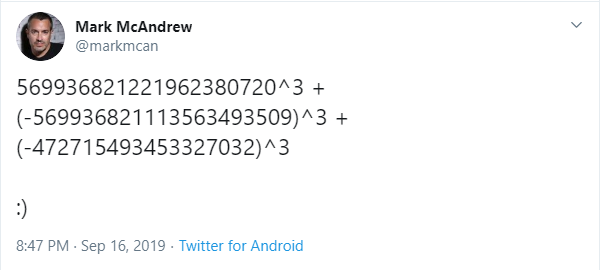
En dat bleek precies $3$ te zijn.