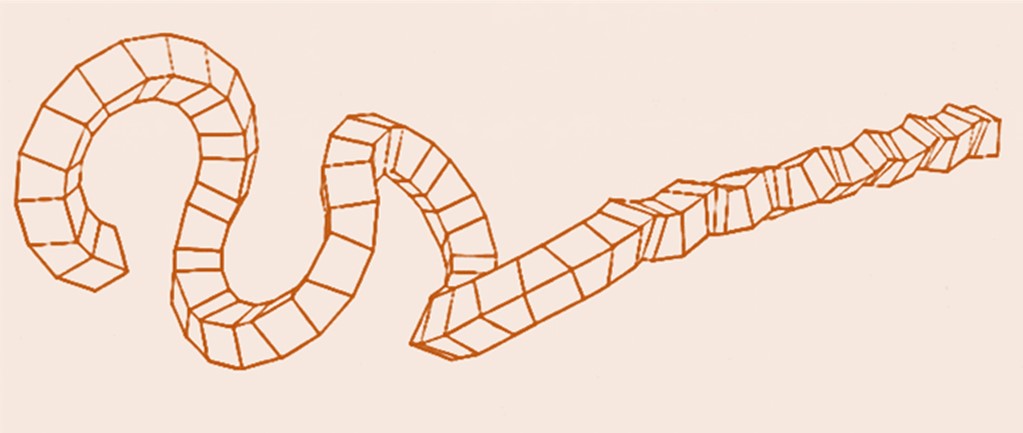
Een komen en gaan

Bij de ingang van een woonwijk in mijn woonplaats Heemskerk, langs de Starweg, bevindt zich een tweeledige sculptuur "Een komen en gaan". Het beeld dateert uit 1992 en was de eerste grote opdracht voor kunstenaar Roland de Jong Orlando.
Het beeld bestaat uit twee exact gelijke vormen, die elk uit 72 identieke modules of bouwstenen bestaan.
Vierkante zaagdoorsneden
In het vorige nummer werd bij het beeld Fibonacci Swing uitgegaan van een balk met een vierkante dwarsdoorsnede om tot de daar gebruikte L- en R-modules te komen. Zaag je zo'n vierkante balk door onder een hoek van $30^{\rm o}$ met de dwarsdoorsnede dan is de zaagdoorsnede een rechthoek. Zaag je een vierkante balk tweemaal door onder bij voorbeeld een hoek van $30^{\rm o}$ in tegengestelde richtingen, dan krijg je een blokvormig trapezium (figuur 1). Om dit soort trapeziumvormige blokjes netjes aan elkaar te passen blijf je hoe dan ook in het platte vlak. Met een vierkante zaagdoorsnede is meer mogelijk. Dan kun je echter niet meer van een vierkante balk uitgaan. Om een vierkante zaagdoorsnede van bijvoorbeeld $A$ bij $A$ cm te krijgen bij een zaagrichting $\alpha$ is een balk nodig met een dwarsdoorsnede van $A$ bij $L$. Daarbij is $L = A \times \cos(\alpha)$.

|

|
|
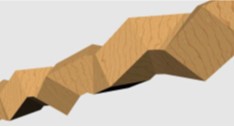
De zo verkregen trapeziumvormige blokjes kunnen dan achtereenvolgens onder hoeken van $90^{\rm o}$, $180^{\rm o}$‚ en $270^{\rm o}$ aan elkaar worden gezet (figuur 2). Zo kunnen ze bij voorbeeld aan elkaar gekoppeld worden door elk volgend blokje met de wijzers van de klok mee over $90^{\rm o}$ te draaien ten opzichte van het voorgaande blokje. Op die manier ontstaat een soort gedraaide of getordeerde balk (figuur 3).

|

|

|
Dat kan ook afgewisseld worden door een volgend blokje $90^{\rm o}$ 'tegen de klok in' te draaien en het daaropvolgende weer $90^{\rm o}$ 'met de klok mee' te draaien,
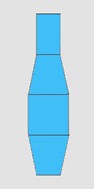
enzovoorts. Dat levert een stukje van een cirkelboog zoals in figuur 4. Daarin zijn de trapeziumvormige modules gemaakt uit een balk van $10$ bij $9{,}7\ cm$ met zaagsneden onder hoeken van $14^{\rm o}$. Afhankelijk van de zaaghoek zal zo'n cirkelboog flauwer zijn en al dan niet tot een cirkel sluiten. Met de blokjes van figuur 4 lukt dat niet. Wel leveren $18$ van die blokjes een bijna sluitende cirkel (figuur 5). Twee van die bijna sluitende cirkels kunnen ook met de uiteinden aan elkaar worden gekoppeld (figuur 6). Dat levert een ruimtelijker geheel. Door combinatie van drie cirkelbogen als in figuur 5, samen met een stuk van de getordeerde balk uit figuur 3, kom je uiteindelijk uit op het ontwerp voor Een komen en gaan (figuur 8).
De twee delen van de sculptuur van Een komen en gaan hebben elk afmetingen van $2{,}35\ m$ hoog, $3{,}80\ m$ breed en $10{,}20\ m$ lang en zijn uitgevoerd in staal. Zoals al aangegeven bestaat elk deel uit $72$ identieke trapeziumvormige modules denkbeeldig verkregen door een grote stalen balk (die net niet vierkant is op de dwarsdoorsnede) onder hoeken van $14^{\rm o}$ door te zagen. Zo'n balk bestaat natuurlijk niet. Voor elke module moesten dus steeds vier platen tot een koker aan elkaar worden gelast. Oftewel: twee identieke trapeziumvormige platen, een rechthoekige en een vierkante (figuur 7). De 'onderkant' van deze trapeziumvormige modules is ook een vierkant met dezelfde afmetingen als de vierkante denkbeeldige zaagdoorsneden. In totaal waren er dus $2 \times 72 \times 4 = 576$ platen nodig die stuk voor stuk aan elkaar gelast moesten worden.