
Een priemzeef van cirkels
In dit artikel bekijken we een meetkundige constructie om twee positieve reële getallen te vermenigvuldigen, en zien we een leuke toepassing als 'priemzeef'.
Constructie(naar een artikel van Mihai Prunescu): Neem twee positieve reële getallen $a$ en $b$. Zoals bekend gaat er door drie gegeven punten die niet op één en dezelfde rechte lijn liggen een unieke cirkel. Teken in het $(x, y)$-vlak de cirkel die wordt bepaald door de drie punten $(-a, 0)$, $(0, -1)$ en $(b, 0)$. Deze cirkel snijdt de positieve $y$-as in het punt $(0, y)$, waarbij $y = ab$ het product is van de getallen $a$ en $b$. |
||||
De opgaven onderaan zullen je helpen deze bewering te bewijzen.
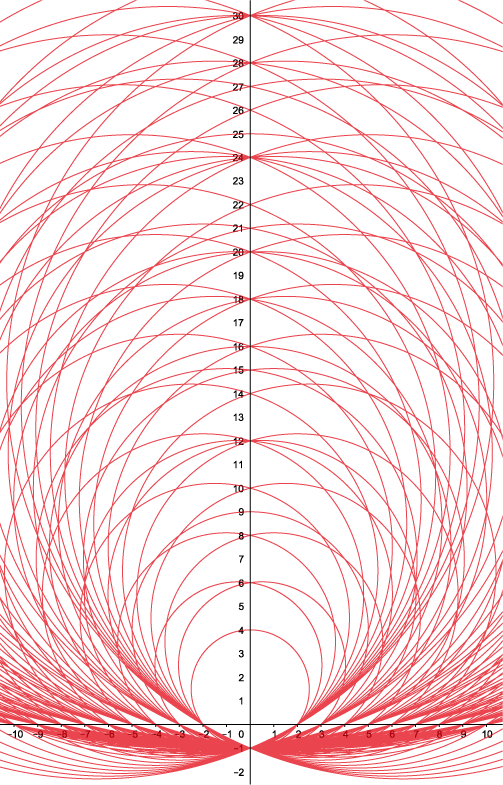
Stel je voor dat we de factoren $a$ en $b$ laten lopen over alle natuurlijke getallen groter dan $1$. De $y$-coördinaat $ab$ van het snijpunt van de bijbehorende cirkel met de positieve $y$-as bereikt dan alle samengestelde natuurlijke getallen, die een product zijn van getallen groter dan $1$, maar gaat voorbij aan de priemgetallen, die alleen deelbaar zijn door $1$ en zichzelf. De cirkels door $(-2, 0)$ en $(2, 0)$ strepen van de natuurlijke getallen op de $y$-as alle tweevouden weg, de cirkels door $(-3, 0)$ en $(3, 0)$ alle drievouden, enzovoort (zie figuur 1). Alleen de priemgetallen blijven over. De cirkels vormen als het ware een priemzeef, een raster dat ten opzichte van de natuurlijke getallen op de $y$-as gaten heeft precies bij de priemgetallen. Er zijn overigens ook andere priemzeven bekend. Ze zijn in zekere zin complementair aan de zeef van Goldbach in het vorige nummer van Pythagoras.
|
Priemzeef bestaande uit cirkels. De cirkel door de punten $(-a, 0)$, $(0, -1)$ en $(b, 0)$ gaat door het punt
|
Opgave 1$Bewijs\ door\ berekening$ De algemene vergelijking van een cirkel in het $(x, y)$-vlak is $(x - u)^2 + (y - v)^2 = r^2$, waarbij $(u, v)$ het middelpunt is en $r$ de Het snijpunt met de positieve $y$-as volgt uit de vergelijking van de cirkel door $x = 0$ te stellen, maar het is eleganter goed naar de cirkel te kijken en op te merken dat dit snijpunt even ver boven Leid hieruit af dat $y = ab$. |
|
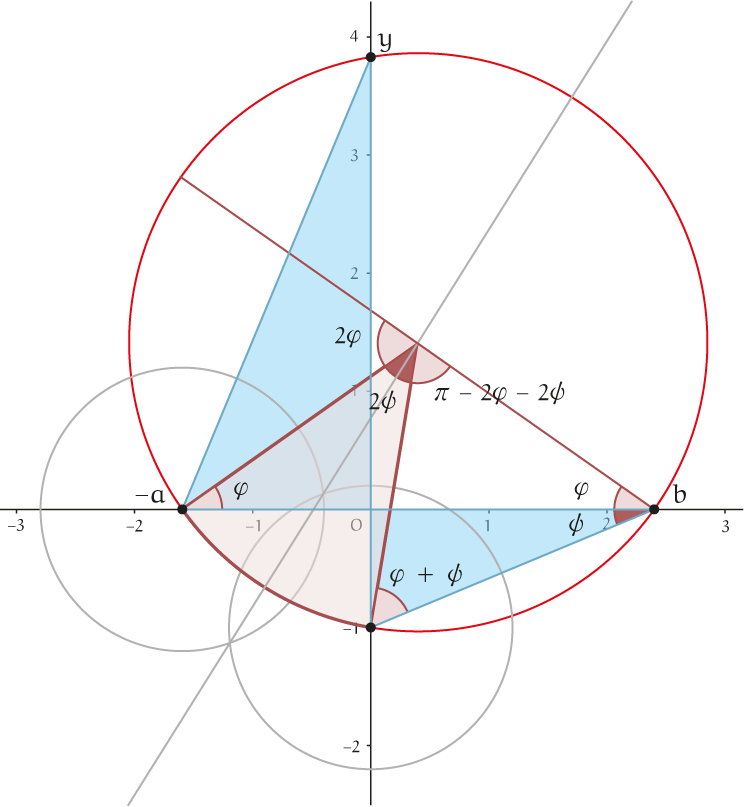
De cirkel door de punten $(-a, 0)$, $(0,-1)$ en $(b, 0)$ gaat door het punt $(0, ab)$: de blauwe driehoeken zijn gelijkvormig, waaruit volgt dat $y = ab$. |
Opgave 2$Bewijs\ met\ passer\ en\ liniaal$ Hoe kun je met alleen een liniaal zonder schaalverdeling en een passer de cirkel door de drie punten $(-a, 0)$, $(0, -1)$ en $(b, 0)$ construeren? Figuur 2 geeft een aanwijzing. Teken twee We tonen aan dat de driehoek met hoekpunten $(-a, 0)$, $(0, 0)$, $(0, y)$ en de driehoek met hoekpunten $(0, -1)$, $(0, 0)$, $(b, 0)$ gelijkvormig zijn. Ga na dat daaruit direct volgt dat $y = ab$. De gelijkvormigheid tonen we aan door te bewijzen dat de hoeken waaronder de cirkelboog tussen $(-a, 0)$ en $(0, -1)$ wordt gezien vanuit $(b, 0)$ en vanuit $(0, y)$ gelijk zijn. Ga uit van de hoeken $\varphi$ en $\psi$, en leidt de andere aangegeven hoeken af; gebruik dat hoeken die samen een rechte lijn opspannen evenals de drie hoeken van een driehoek optellen tot $\pi$ radialen. De conclusie is dat de omtrekshoek $\psi$ vanuit $(b, 0)$ op de cirkelboog gelijk is aan de helft van de middelpuntshoek op de cirkelboog. Evenzo is ook de omtrekshoek vanuit $(0, y)$ gelijk aan de halve middelpuntshoek. Daarmee is het bewijs rond. |
