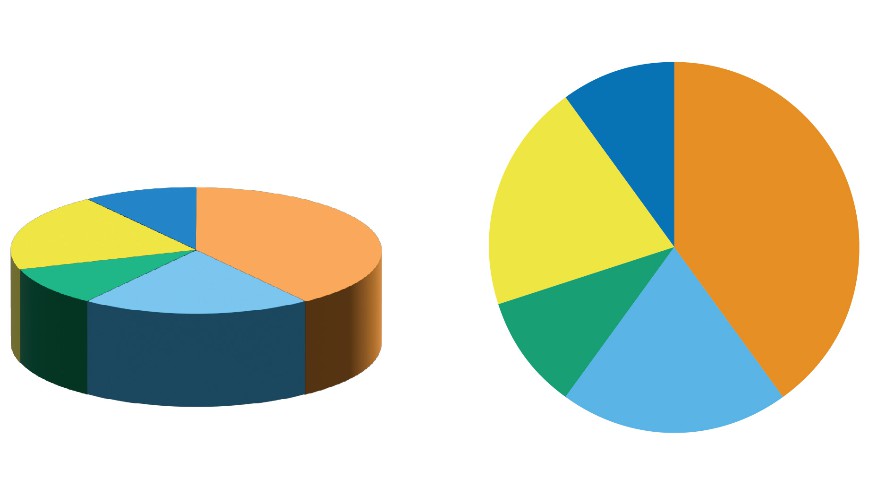
Eerste hulp bij nepnieuws met misleidende grafieken
[oOO]
Grafieken zijn heel geschikt om veel en complexe informatie weer te geven: ze bieden in één oogopslag overzicht en duidelijkheid. Bovendien hebben ze een objectieve uitstraling waardoor ze het vaak goed doen als argument bij een bewering: "De cijfers liegen niet." Behalve als ze dat wel doen, en dat komt helaas maar al te vaak voor. Daarom hier een lesje in het doorprikken van nepnieuws met misleidende grafieken.
Om jezelf tegen misleiding te wapenen is het handig iets te begrijpen van hoe wij grafieken uitlezen. Hoewel vrijwel iedereen beweert gewoon goed naar de cijfers te kijken, blijkt uit onderzoek dat dat eigenlijk pas stap twee is in het leesproces. Zodra je een grafiek onder ogen krijgt start eerst een intuïtieve fase van lezen: het vormen van een oordeel op basis van je eerste indruk. Dat wil zeggen dat je direct al een inschatting maakt van welk verhaal de grafiek je vertelt door puur af te gaan op het beeld dat de grafiek je voorschotelt. Zie je een opgaande lijn?
Dan is er een toename van het een of ander. Zijn er staven van verschillende lengten? Dan is er van het één meer dan van het ander. Dit soort van oordelen hebben we geleerd te maken van kleins af aan, door onze interactie met de wereld om ons heen: klim je een heuvel op dan win je aan hoogtemeters en van het grootste koekje uit de trommel kun je het langste genieten. Pas als we dit oordeel hebben geveld treedt de tweede fase van grafieken uitlezen in werking en gaan we kijken naar de assen en de labels en proberen we precieze cijfers af te lezen.
Misleidende grafieken hebben je vaak al te pakken in die eerste fase, doordat ze je een verkeerd beeld voorschotelen. Dat doen ze bijvoorbeeld door een misleidend perspectief te gebruiken, door met de assen te knoeien of door zaken weg te laten. Hoe dat er precies uitziet bespreken we zo. Nou denk je misschien dat je die trucjes wel doorziet en dat jij je niet laat vangen, maar dat is helaas niet zo. Onderzoek laat zien dat iedereen – ja, echt iedereen – door zulke grafieken wordt misleid. Als je heel goed bent met grafieken (je grafiekgeletterdheid) en cijfers (gecijferdheid) is het effect wat kleiner. Maar ook bij de knapste koppen heeft een misleidende grafiek effect!
Het probleem van misleiding zit dus in de eerste intuïtieve leesfase en daar doe je niks tegen. De manier om die misleiding door te prikken zit ‘m erin om de misleiding te herkennen en recht te zetten in de tweede fase. Om je daarin te trainen bespreken we hier de drie meest voorkomende manieren van misleiding in grafieken en geven we je een checklist om jezelf mee te wapenen.
3D perspeCtief
Grafieken zijn beelden opgebouwd uit lijnen, vormen, tekst en getallen. Soms worden er plaatjes van het onderwerp aan toegevoegd om de grafiek aantrekkelijker te maken of om snel zichtbaar te maken waar de grafiek over gaat. In de regel zijn grafieken plat, dus tweedimensionaal, zodat ze gemakkelijk zijn af te lezen en verschillende punten goed met elkaar zijn te vergelijken. Schending van deze regel door een driedimensionale grafiek te maken zorgt ervoor dat onderdelen op de voorgrond groter of belangrijker lijken dan die op de achtergrond en aan de zijkanten (zie figuur 1).
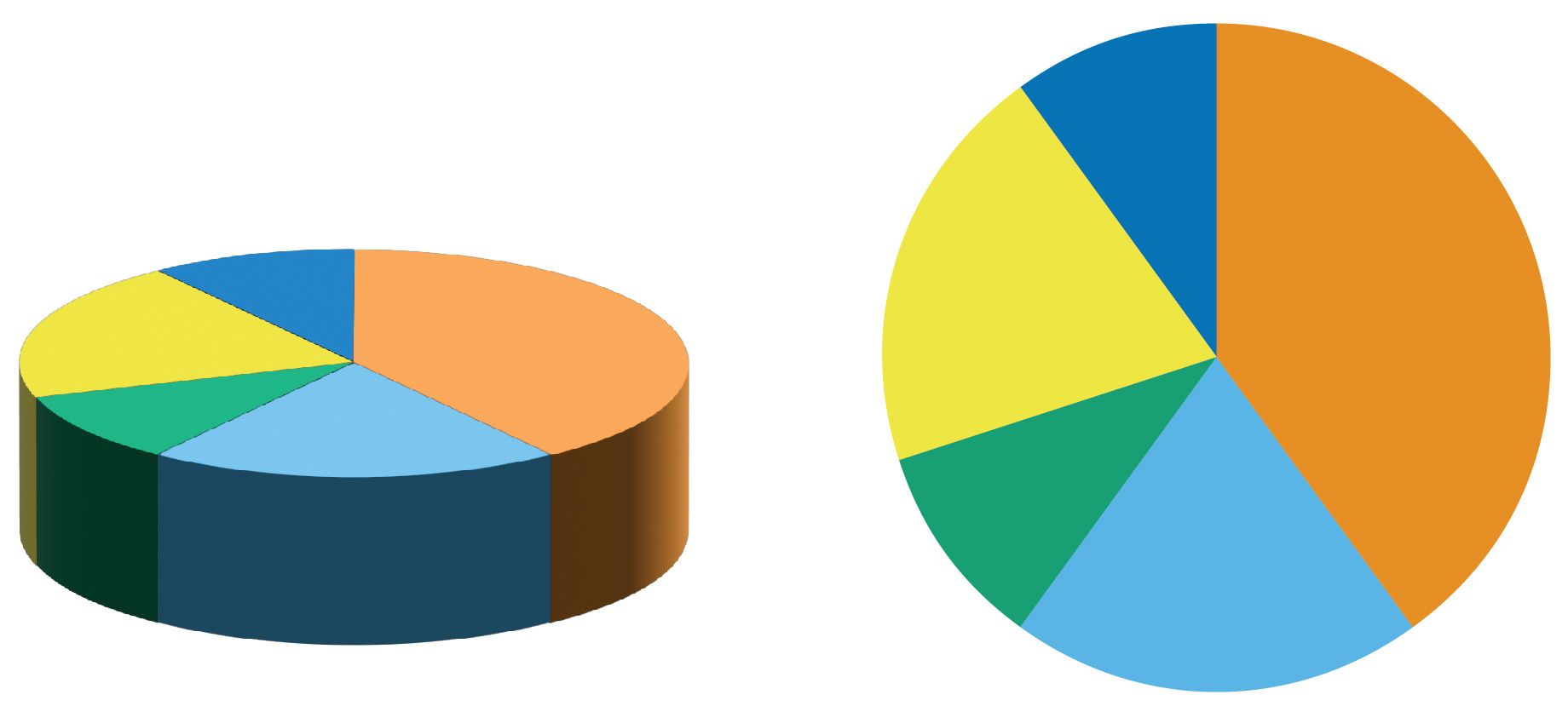
Vreemde assen
Veel grafieken hebben een verticale en een horizontale as. Op beide assen moeten de waarden logisch gekozen zijn en in gelijke stappen verdeeld zijn.
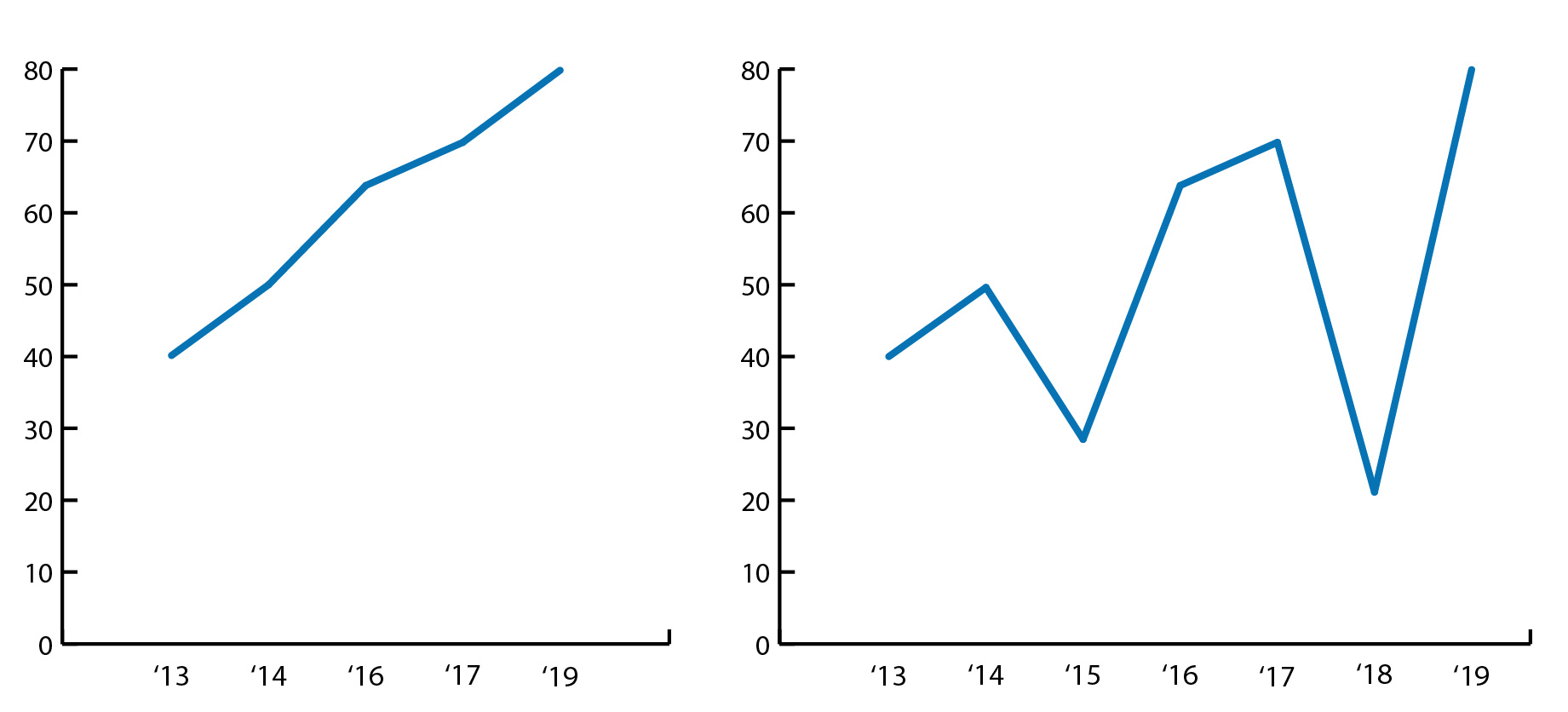
Op de horizontale as staan bijvoorbeeld verschillende momenten in de tijd om een verloop over een periode weer te geven, of verschillende categorieën die met elkaar worden vergeleken. Als de horizontale as een verloop over tijd weergeeft is die in de regel chronologisch geordend en verdeeld in gelijkmatige stapjes. Een niet-chronologische volgorde zou onlogisch zijn en daardoor een verkeerde indruk van de ontwikkeling over de tijd wekken (zie figuur 2).
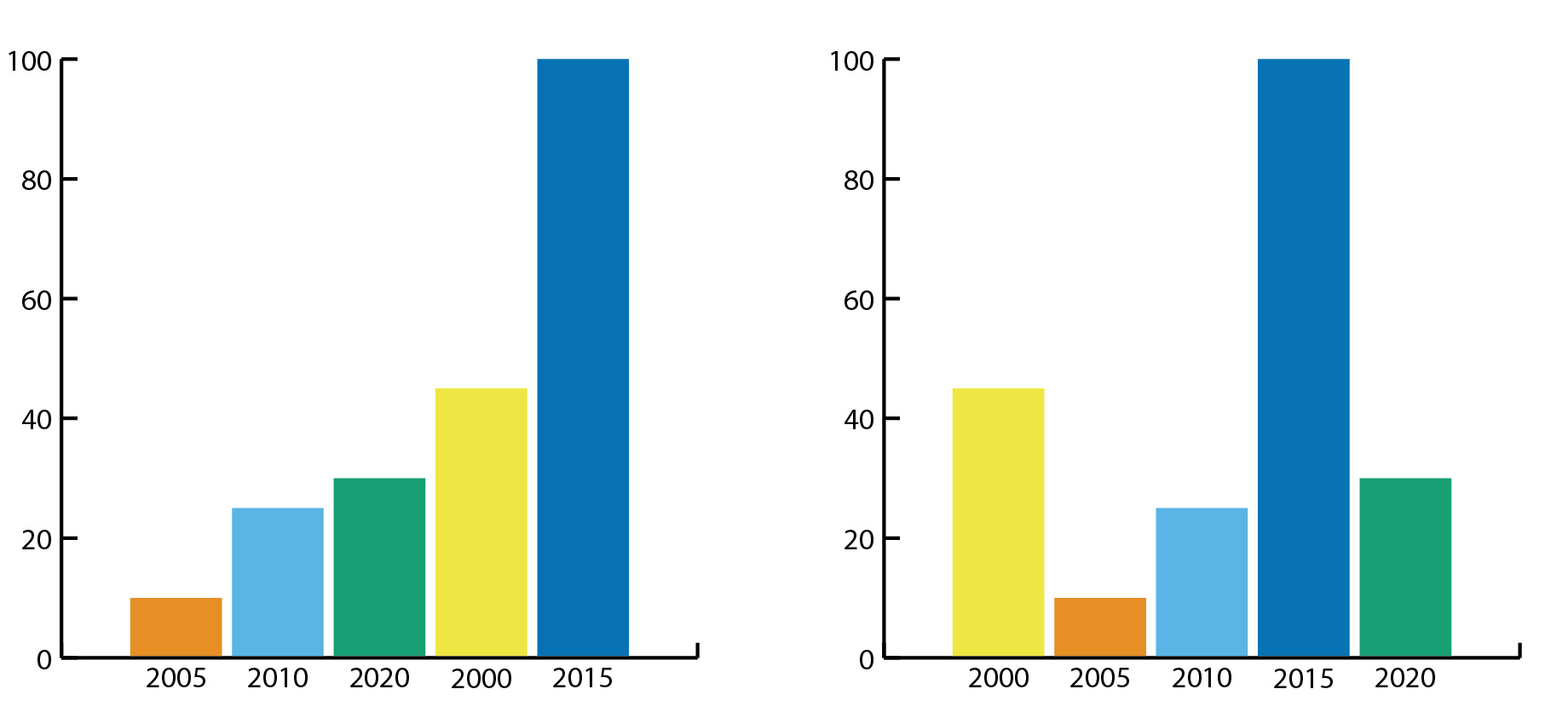
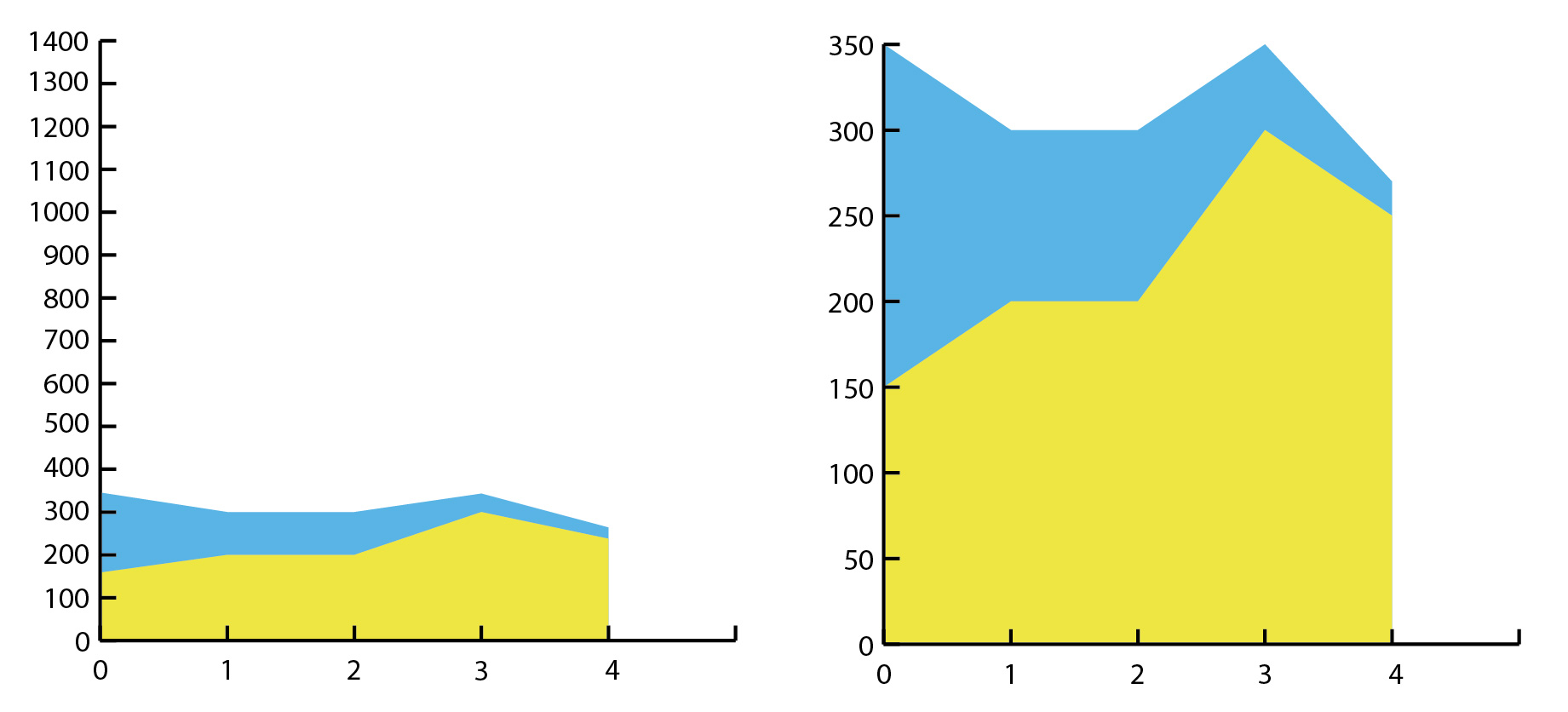
De verticale as geeft vaak de waarde in een bepaalde eenheid weer, zoals percentages, euro's of aantal personen. De minimale en maximale waarden op de as moeten passen bij de data en het interval daartussen moet in gelijke stappen verdeeld zijn. De verticale as begint in de regel op nul (de nullijn). Schending van deze regel door de nullijn weg te laten zorgt er vaak voor dat de verschillen tussen de waarden groter lijken (zie figuur 3). De as eindigt meestal rond de grootste waarde, zodat het hele oppervlak van de grafiek wordt benut, van onder tot boven. Als je een veel groter maximum kiest, lijken de verschillen tussen de data juist kleiner (zie figuur 4).
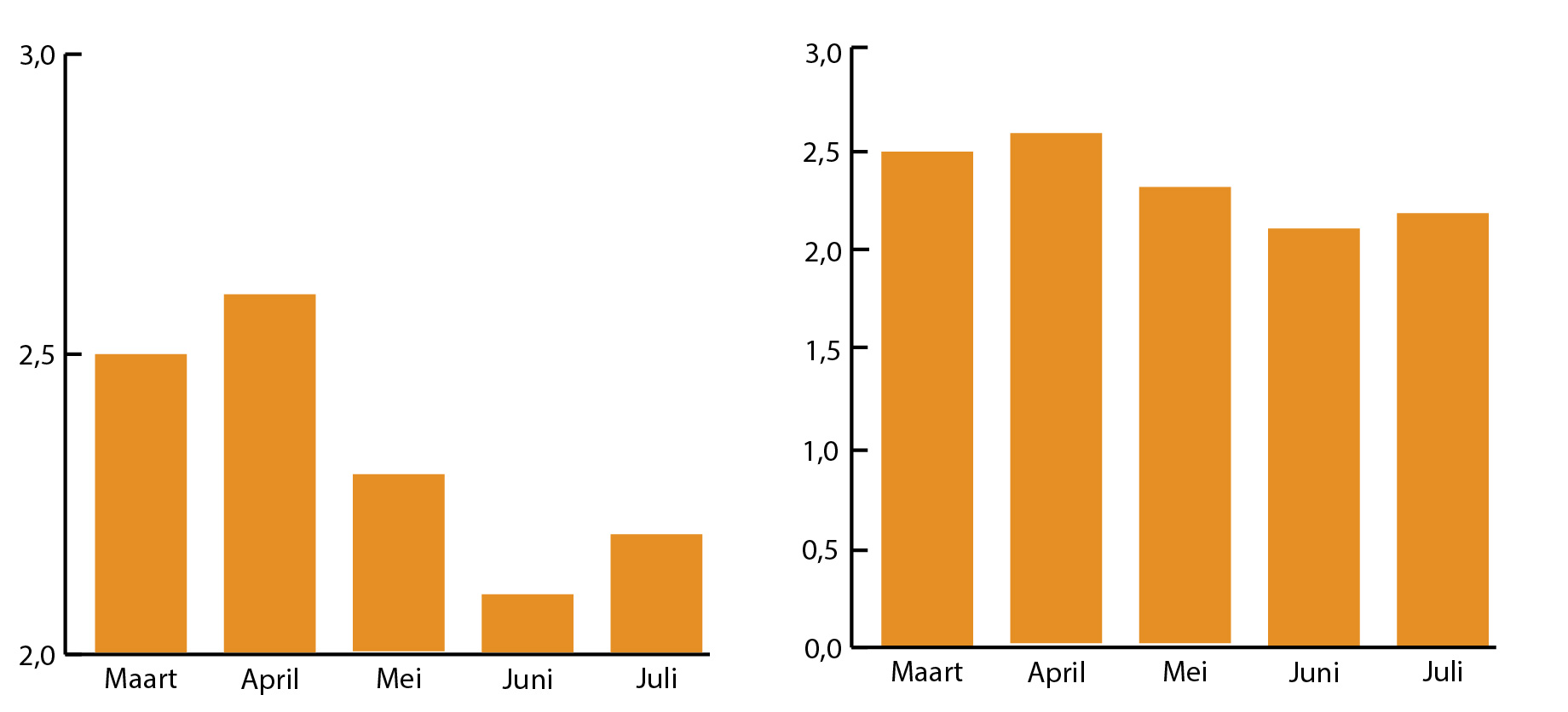
Cherry piCking
Een grafiek kan er heel netjes uitzien met een mooie spreiding, een nullijn en een heldere tweedimensionale opmaak en toch misleidend zijn, doordat het niet het hele verhaal vertelt. De cijfers die erin staan kloppen dan wel, maar er is veel informatie weggelaten. Dit type misleiding is niet altijd makkelijk te doorzien, maar door te kijken naar de waarden op de assen of naar de legenda in taartdiagrammen (die laat zien wat elke kleur weergeeft) kun je daar wel een idee
van krijgen. In de regel hebben horizontale assen een gelijkmatig interval (stapjes) waarbij geen punten ontbreken. Bij schending van deze regel laat de grafiek een ontwikkeling zien die niet klopt (zie figuur 5). In taartdiagrammen en staafdiagrammen die categorieën vergelijken staan in de regel alle belangrijke categorieën. Schending van deze regel zorgt voor een scheef beeld in de onderlinge verhoudingen (zie figuur 6).
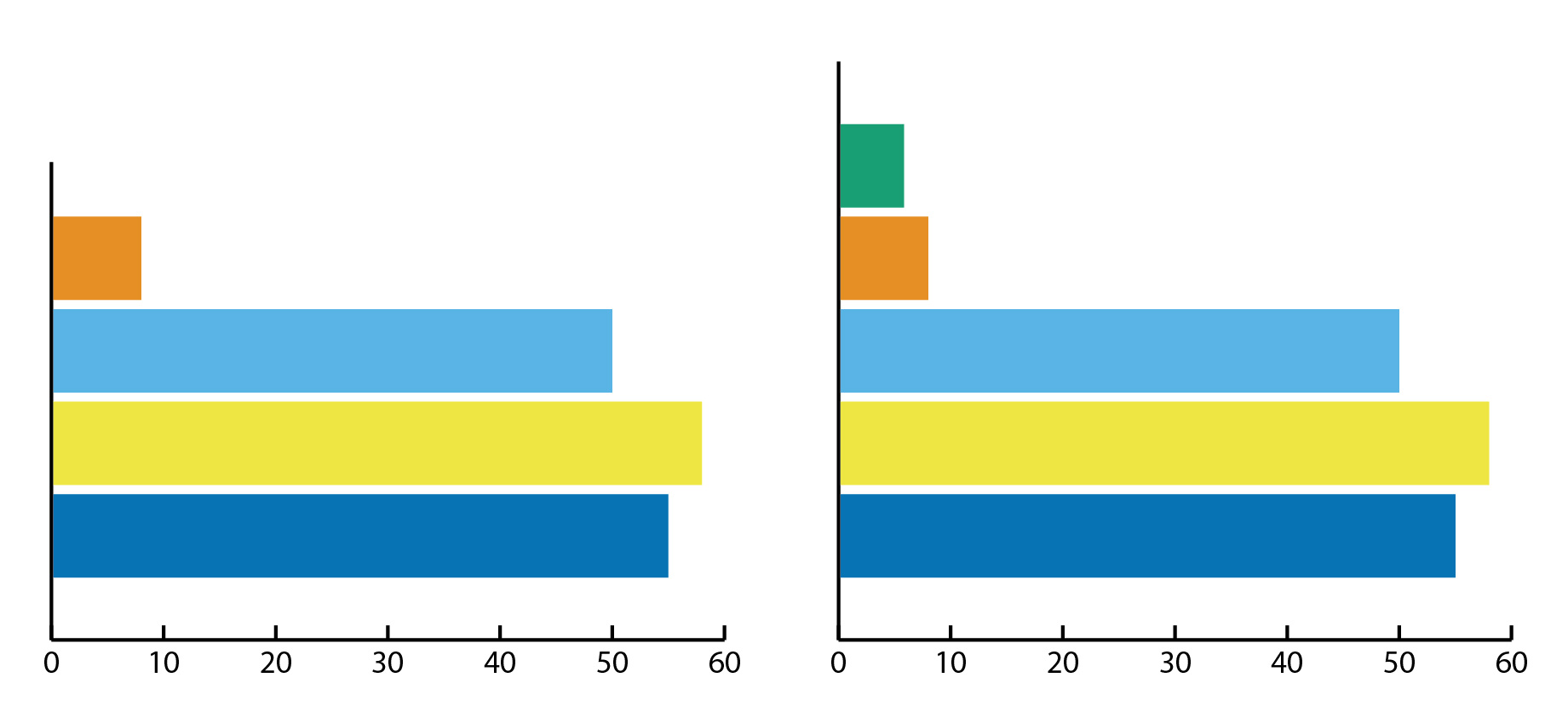
CheCklist
Met deze checklist kun je jezelf tegen misleiding wapenen.
- Is de grafiek in 2D weergegeven?
- Is de horizontale as chronologisch geordend?
- Begint de verticale as op nul?
- Is de stapgrootte op de verticale as passend voor de spreiding van de data?
- Zijn de stappen op de assen gelijkmatig verdeeld?
- Zijn de categorieën compleet?
Kom je een grafiek tegen en is het antwoord op één of meerdere van deze vragen "nee", krab jezelf dan achter de oren en wees extra kritisch op de afzender: vraag je af waarom de maker het nodig vindt om ontwerpstandaarden van grafieken te schenden. Is een eerlijke grafiek misschien niet zo overtuigend…?
De GrafiekpolitieOm mensen te beschermen tegen nepnieuws, hebben we onderzocht wat een effectieve methode is om hen te helpen. We hebben een aantal vormen uitgeprobeerd en zagen dat het vooral helpt als het eerste intuïtieve beeld wordt gecorrigeerd door het juiste plaatje ernaast te zetten met een waarschuwing. Maandelijks corrigeren we op deze manier als Grafiekpolitie grafieken die we tegenkomen in het nieuws of op social media en spreken de makers erop aan dat ze hun lezers misleiden. We bespreken op de website van Nieuwscheckers. nl waar het misgaat en waarom dat misleidend is. Daar vind je ook meer informatie over ons onderzoek. Laat jezelf niet neppen en volg de Grafiekpolitie op www.nieuwscheckers.nl! 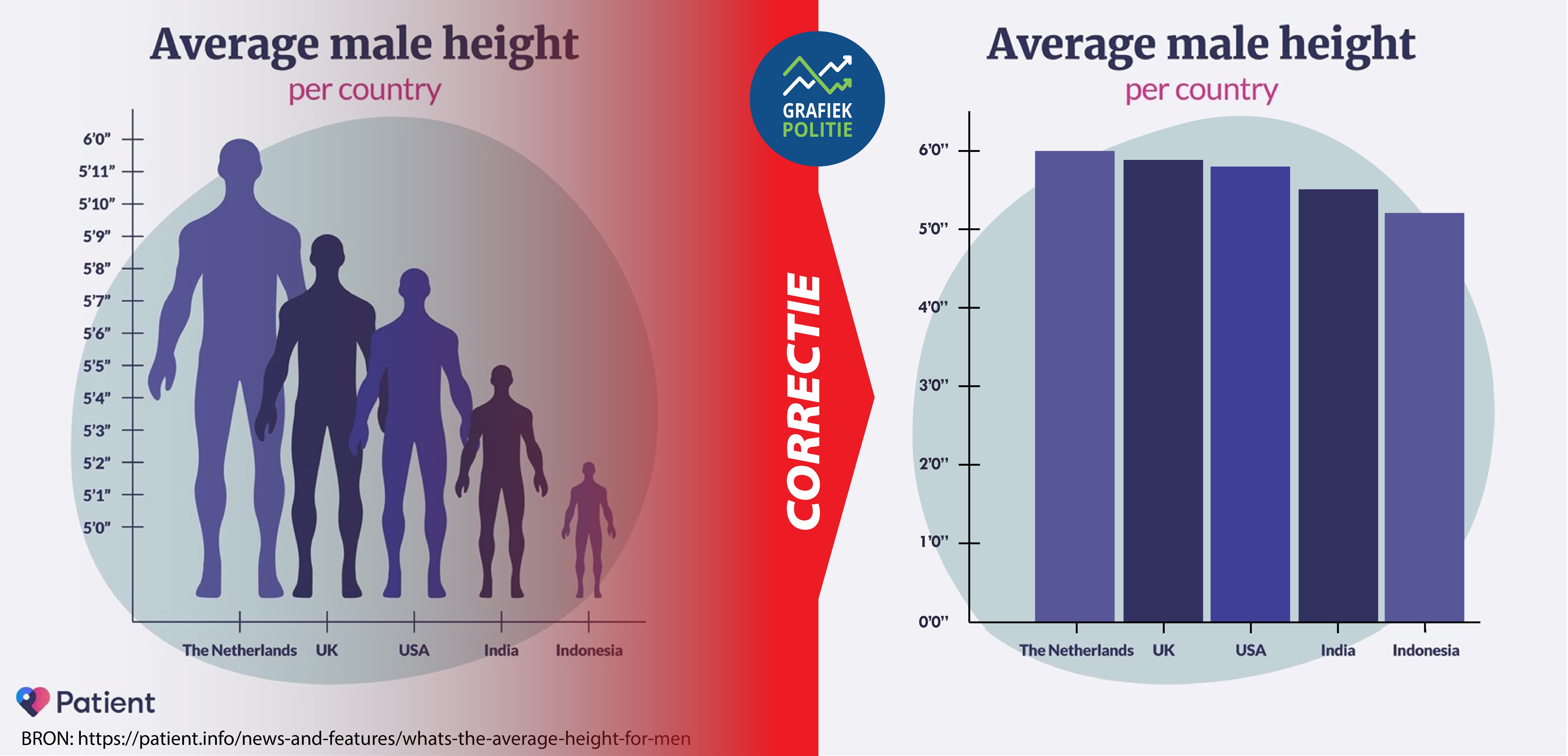
|
||||
