Voor fabrikanten is het nuttig om te weten hoe je met zo weinig mogelijk verpakkingsmateriaal een maximale inhoud kunt verpakken. Voor de maximale inhoud bij een gegeven oppervlakte kom je al snel uit bij de bol. Een bol zou dus per inhoud het minste verpakkingsmateriaal kosten, maar een bol als verpakking is natuurlijk niet zo handig. 

Als je kijkt naar een cilindervormig blik kan je uitrekenen wat de minimale oppervlakte is bij een gegeven inhoud. Als je het grondvlak en bovenvlak meerekent zou dat er als volgt uit kunnen zien. 

Voorbeeld Cilinder

Gegeven een cilindervormig blik met een inhoud van 1 liter. Wat zou de verhouding van de straal van het grondvlak en de hoogte moeten zijn voor een minimale
hoeveelheid blik?

Bij een gegeven straal $r$ en een hoogte $h$ geldt:

$${\rm Inhoud} = \pi r^2h$$

$${\rm Oppervlakte} = 2\pi r^2 + 2\pi rh$$

Als je de inhoud stelt op 1 dm³ dan kun je in de eerste vergelijking $h$ uitdrukken in $r$ en invullen in de tweede vergelijking.

$${\rm Oppervlakte} = \frac{2}{r} + 2\pi r.$$

Differentiëren, de afgeleide op nul stellen en een tekenverloop maken geeft een minimale oppervlakte voor

$$r=\sqrt[3]{\frac{1}{2\pi}}.$$

Dit geeft uiteindelijk een cilinder met straal van $10{,}8\ cm$ én een hoogte van $10{,}8\ cm$. Ik ben benieuwd hoeveel blikken in de winkel hier aan voldoen. Een standaard conservenblik heeft een diameter $9{,}9\ cm$ en hoogte $11{,}7\ cm$. Ongetwijfeld zullen er nog meer zaken meespelen dan alleen het minimaliseren
van het verpakkingsmateriaal, bijvoorbeeld dat je er tien in een schap van 1 meter diep neer kunt zetten. 

VerpakKing

Om verschillende soorten verpakkingen te kunnen vergelijken zou het handig zijn een maat te hebben voor de effectiviteit van een verpakking, bijvoorbeeld uitgedrukt in procenten. De bol zou dan een effectiviteit hebben van $100\%$. Maar wat zou de effectiviteit van een kubus zijn? Van een prisma? Een piramide? Of van de cilinder hierboven? Een melkpak? Een pak koffie?

Mijn idee is om te kijken naar de oppervlakte van je object en te kijken naar de verhouding van de werkelijke inhoud en de inhoud als je met die oppervlakte een bol
zou maken. Je weet dan hoeveel procent van de mogelijke inhoud je gebruikt en dat is dan je maat voor de effectiviteit. 

EfFeCtiviteit van de Cilinder

De cilinder met de minimale oppervlakte hierboven heeft (bij benadering) een oppervlakte van $5{,}53\ dm^2$ en een inhoud van $1\ dm^3$. Een bol met een oppervlakte van $5{,}5\ dm^2$ heeft een straal van ongeveer $0{,}66\ dm$. De inhoud van die bol zou dan ongeveer $1{,}2\ dm^3$ zijn. 

Nu moet je de werkelijke inhoud delen door de inhoud van onze denkbeeldige bol om de effectiviteit te berekenen. De effectiviteit is ongeveer gelijk aan 

$$1{,}2 \times 100\% = 83\%$

Formule

Mooi zou het zijn als je er een formule voor zou kunnen bedenken.

$${\rm effectiviteit} = \frac{\rm inhoud\ van\ het\ lichaam}{\rm inhoud\ als\ het\ een\ bol\ zou\ zijn}\times 100\%.$$

Voor de '${\rm inhoud\ als\ het\ een\ bol\ zou\ zijn}$' heb je de straal nodig:

$$r=\sqrt{\frac{\rm oppervlakte}{4\pi}}.$$

De inhoud van de denkbeeldige bol is dan gelijk aan:

$$I=\frac{4}{3}\pi\left(\sqrt{\frac{\rm oppervlakte}{4\pi}}\right)^3.$$

Invullen in de vergelijking hierboven geeft:

$${\rm effectiviteit}=\frac{\rm inhoud\ van\ het\ lichaam}{\frac{4}{3}\pi\left(\sqrt{\frac{\rm oppervlakte}{4\pi}}\right)^3}\times 100\%.$$

De formule laat zich vereenvoudigen tot:

$${\rm effectiviteit}=\frac{6\sqrt{\pi}\times {\rm inhoud}}{\sqrt{{\rm oppervlakte}^3}}\times 100\%.$$

Met deze formule kan je dan snel uitrekenen wat de effectiviteit van een verpakking is.

Voorbeelden

lichaam		oppervlakte		inhoud		effectiviteit
Kubus van $1\times 1\times 1$		$6$		$1$		$72,4\%$
Balk van $1\times 2\times 3$		$22$		$6$		$61,8\%$
Bol met straal $2$		$50{,}3$		$33{,}5$		$100,0\%$
Kegel met straal $2$ en hoogte 6(1)		$52{,}3$		$25{,}1$		$70,7\%$
Gelijkzijdige piramide met zijde $3$ en hoogte $4$(1)		$52$		$21$		$59,6\%$
Cilinder met straal $2$ en hoogte $4$(2)		$75{,}4$		$50{,}3$		$81,6\%$

⁽¹⁾ inclusief grondvlak ⁽²⁾ inclusief boven- en grondvlak

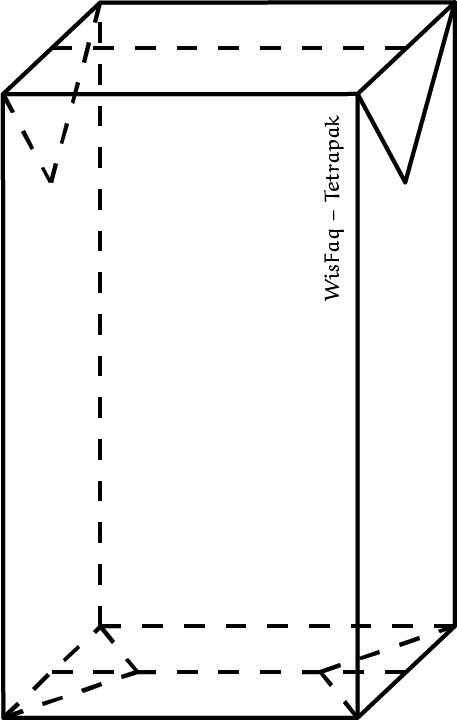
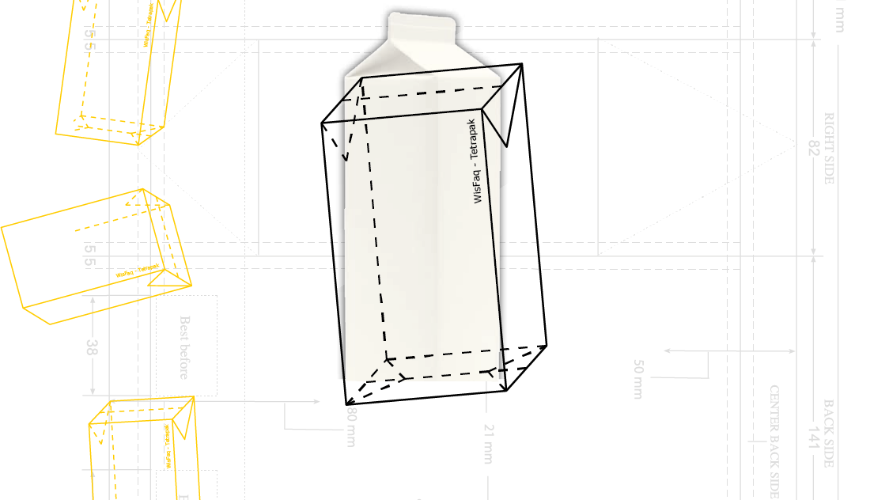
Opgave Ik heb een rechthoekig karton van $33\ cm$ bij $54\ cm$. Daarvan kun je verschillende Tetrapakken (zie de figuur) maken. Welk pak heeft de grootste inhoud? Wat is de effectiviteit van z'n pak?

Bekijk oplossing