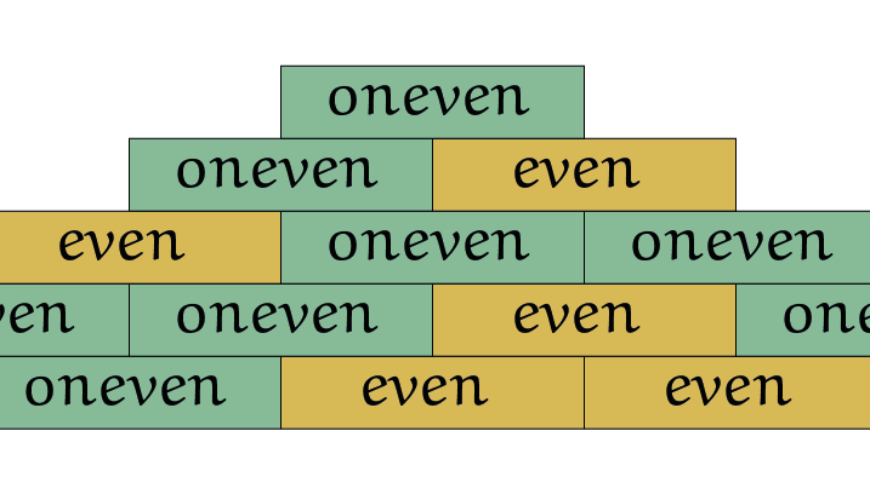
Even en oneven
Ogenschijnlijk eenvoudige vragen zijn soms niet zo eenvoudig te beantwoorden. Bijvoorbeeld het op elkaar leggen van twee soorten blokken. Gelukkig is er Python, waarmee we een programmaatje kunnen maken om sneller een patroon te ontdekken.
We gaan blokken stapelen. De blokken zijn er in twee soorten, laten we zeggen dat we blokken hebben met de tekst even en
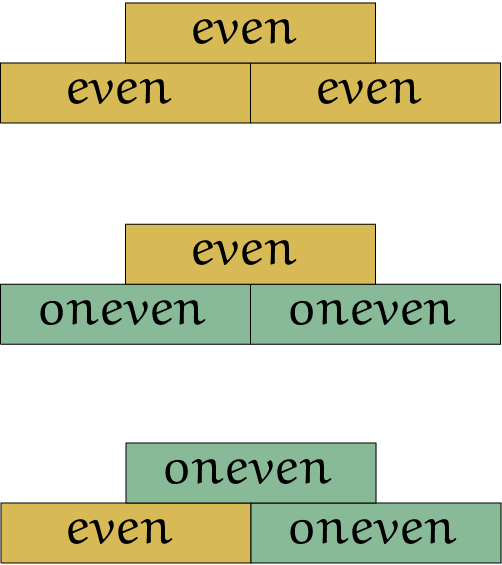
oneven. Leg een aantal blokken naast elkaar op de grond. Leg steeds blokken op een laag hoger, zo dat de helft van het nieuwe blok op een blok er onder rust en de andere helft op een aangrenzend blok. Of er gekozen wordt voor het blok
met even of oneven is hangt af van de twee blokken er onder. Zie de tabel en figuur 1.
| blok L | blok R | nieuw blok |
| $even$ | $even$ | $even$ |
| $oneven$ | $even$ | $oneven$ |
| $even$ | $oneven$ | $oneven$ |
| $oneven$ | $oneven$ | $even$ |
Wat willen we onderzoeken?
Een aantal blokken (zeg $n$) liggen in een rij. Daar bovenop komen $n-1$ blokken te liggen, daarop $n-2$, en bovenop $1$ blok. Bepaal voor elke $n$ hoe je op de grond de blokken moet neerleggen, zodat er in het gehele bouwwerk zoveel mogelijk oneven blokken komen te liggen.
Stel dat de opdracht zou zijn om zoveel mogelijk even blokken te gebruiken, dan is de oplossing eenvoudig, want dan leg je op de grond ook even blokken en heb je een toren met louter even blokken.
Maar als je op de grond alleen oneven blokken legt dan zal de rest van de toren alleen even blokken bevatten. Je moet dus kiezen voor een mix van even en oneven blokken.
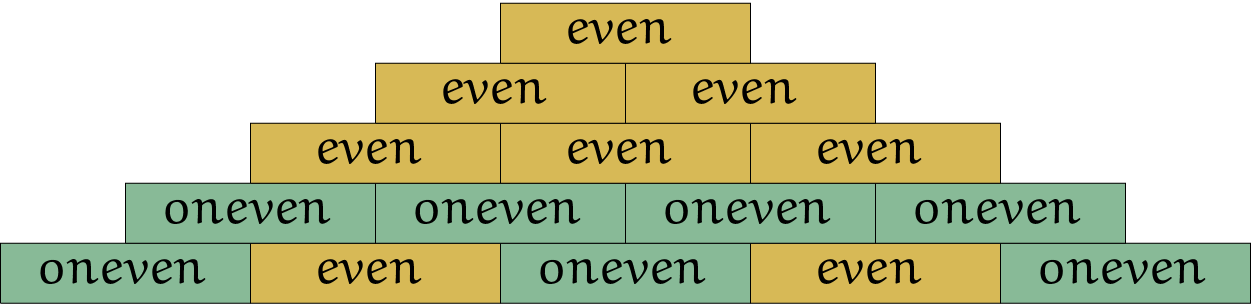
In figuur 2 staat het voorbeeld met 5 blokken.
|
|
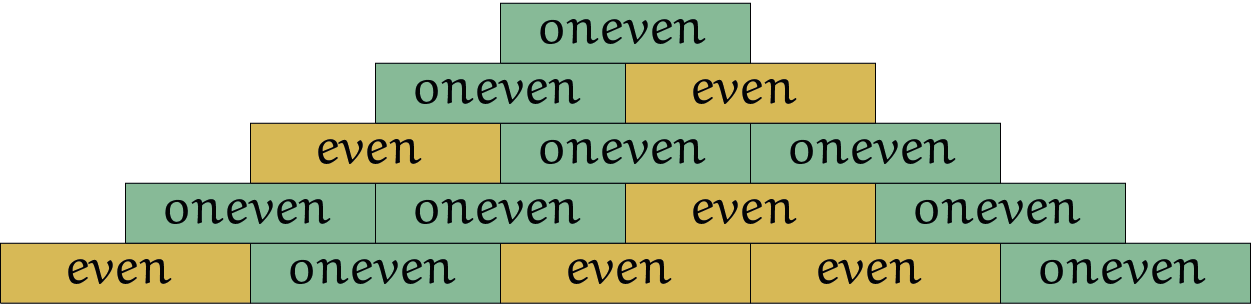
Maar je kunt meer oneven blokken kwijt door op de grond de even en oneven blokken op een andere manier neer te leggen, zoals in figuur 3.
Nu is de vraag hoe moet je de even en oneven blokken rangschikken om in de gehele toren zoveel mogelijk oneven blokken te krijgen? We gaan dat doen door alle mogelijkheden uit te proberen. Dus als we op de grond $N$ blokken neerleggen dan kan in principe voor elk blok gekozen worden uit even of oneven, en dat zijn twee mogelijkheden. Voor $N$ blokken zijn dat dus $2^N$ mogelijkheden. Qua tijd betekent dat dat we als $N$ met $1$ wordt vergroot de tijd verdubbelt. Het zal snel niet meer mogelijk zijn alle mogelijkheden uit te proberen. Uiteraard heeft dat ook te maken met de snelheid van je computer.
Om alle mogelijkheden te kunnen uitproberen zijn er meerdere methodes. We kunnen bijvoorbeeld gebruik maken van de procedure $AlleDeelVerzamelingen(S)$, die alle deelverzamelingen van $S$ genereert. Elk van deze deelverzamelingen staat voor een verzameling van oneven blokken. We bouwen de gehele toren af en tellen het totaal aantal oneven blokken.
We kunnen de opeenvolgende even en oneven blokken weergeven met nullen en enen. In feite staan er nu binaire getallen. Met de functie $bin(n)$ kun je $n$ omzetten in een binair getal. Vervolgens zet je dit binaire getal om in een array met nullen en enen. Deze methode maakt het programma wel iets trager.
Resultaten
De kolommen maximaal aantal oneven blokken en aantal oplossingen zijn terug te vinden op de website van Online Encyclopedia of Integer Sequences (OEIS).
- A007980: max oneven blokken: $[1, 2, 4, 7, 10, 14, 19, 24, 30, 37, 44, 52, 61, 70, 80, 91, 102, 114, 127, 140]$
- A164359: aantal oplossingen: $[1, 3, 3, 2, 3, 3, 2, 3, 3, 2, 3, 3, 2, 3, 3, 2, 3, 3, 2, 3]$
Je ziet ongetwijfeld wel de regelmaat. En dan is het natuurlijk de vraag gaat die regelmaat verder als $n$ groter wordt. Kun je dat wiskundig bewijzen? Dat is best nog een lastige vraag, maar zonder het programma was het nog lastiger geweest!
Meer uitdagingen
Nu kun je je ook afvragen: wat gebeurt er als je in plaats van twee soorten blokken drie soorten blokken hebt. Blokken met waarde $0$, $1$ en $2$. Boven op twee blokken komt een blok met de som van die twee blokken, en mocht die som drie of meer zijn, dan trek je er drie van af. Hoe ziet de rij blokken er uit als je de som van alle waarden van blokken wilt maximaliseren? En uiteraard, in plaats van drie soorten blokken kun je ook vier, vijf, zes, … soorten blokken kiezen.
| $n$ | max oneven | aantal opl. | oplossingen |
| $1$ | $1$ | $1$ | $1$ |
| $2$ | $2$ | $3$ | $01$ |
| 3 | 4 | 3 | 011 |
| 4 | 7 | 2 | 1011 |
| 5 | 10 | 3 | 01101 |
| 6 | 14 | 3 | 011011 |
| 7 | 19 | 2 | 1011011 |
| 8 | 24 | 3 | 01101101 |
| 9 | 30 | 3 | 011011011 |
| 10 | 37 | 2 | 1011011011 |
| 11 | 44 | 3 | 01101101101 |
| 12 | 52 | 3 | 011011011011 |
| 13 | 61 | 2 | 1011011011011 |
| 14 | 70 | 3 | 01101101101101 |
| 15 | 80 | 3 | 011011011011011 |
| 16 | 91 | 2 | 1011011011011011 |
| 17 | 102 | 3 | 01101101101101101 |
| 18 | 114 | 3 | 011011011011011011 |
| 19 | 127 | 2 | 1011011011011011011 |
| 20 | 140 | 3 | 01101101101101101101 |
Hieronder, onder het kopje [Documenten], kun je de bijbehorende Python code vinden.
