Fermat in de Polder
Drie families op het platteland ver weg van alles willen iets doen tegen de opwarming van de aarde en nemen een moedig besluit. Zij gaan een windmolen bouwen en hopen hiermee al hun elektriciteit zelf te kunnen produceren. Zij mogen wel heel sociaal bewust zijn maar ze zijn niet dom. Ze vragen gelijk subsidie aan. Een subsidie is mogelijk maar er zijn voorwaarden. De belangrijkste is dat ze moeten aantonen dat ze de kosten zo laag mogelijk hebben gehouden. Zij hebben gekozen voor de meest efficiënte windmolen met de beste prijs-kwaliteitverhouding. Die kosten geven geen probleem. Maar er zijn ook kosten die niet van tevoren vaststaan. De belangrijkste daarvan is de bekabeling van de windmolen naar de drie boerderijen en daarbij is het zaak om de totale lengte van de kabels zo klein mogelijk te houden. Hoe moeten ze die bepalen?
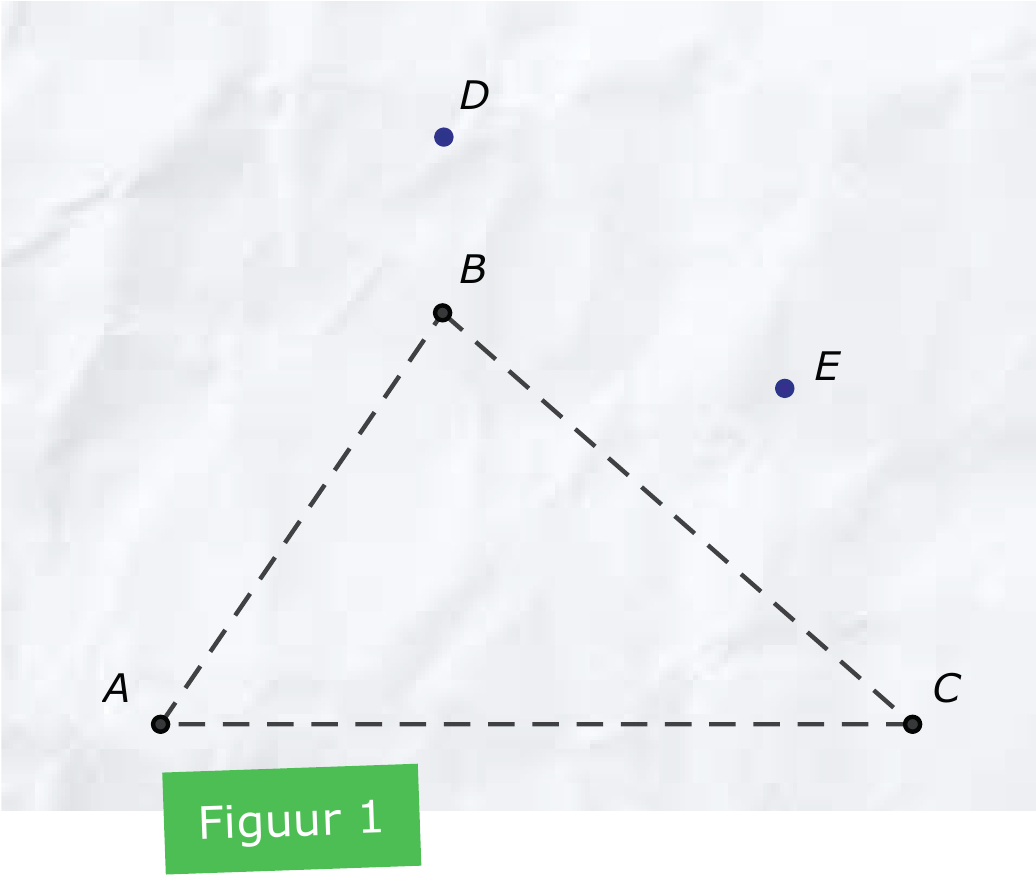
Zoals gezegd wonen deze families op het platteland en dus vrij ver uit eklaar en niet op een rij naast elkaar. De onderlinge afstanden tussen hun huizen zijn $4$km, $5$km en $6$km. Figuur 1 is een tekening van hun woonsituatie. Hun huizen zijn te vinden op de punten $A$, $B$, en $C$ en tijdens de eerste strategievergadering worden de twee punten $D$ en $E$ buiten driehoek $ABC$ als mogelijke windmolenlocaties besproken.
Opgave 1
Toon aan dat deze locaties geen subsidie in de wacht zullen slepen.
Na deze eerste tegenslag worden locaties op de rand van driehoek $ABC$ onder de loep genomen.
Opgave 2
Waar zijn hier de drie beste locaties en welke is het allerbeste van deze drie?
Nu is het natuurlijk een interessante vraag of betere punten te vinden zijn binnen driehoek $ABC$. Dit is helaas een veel moeilijkere vraag mede door het feit dat driehoek $ABC$ niet symmetrisch is.
Opgave 3
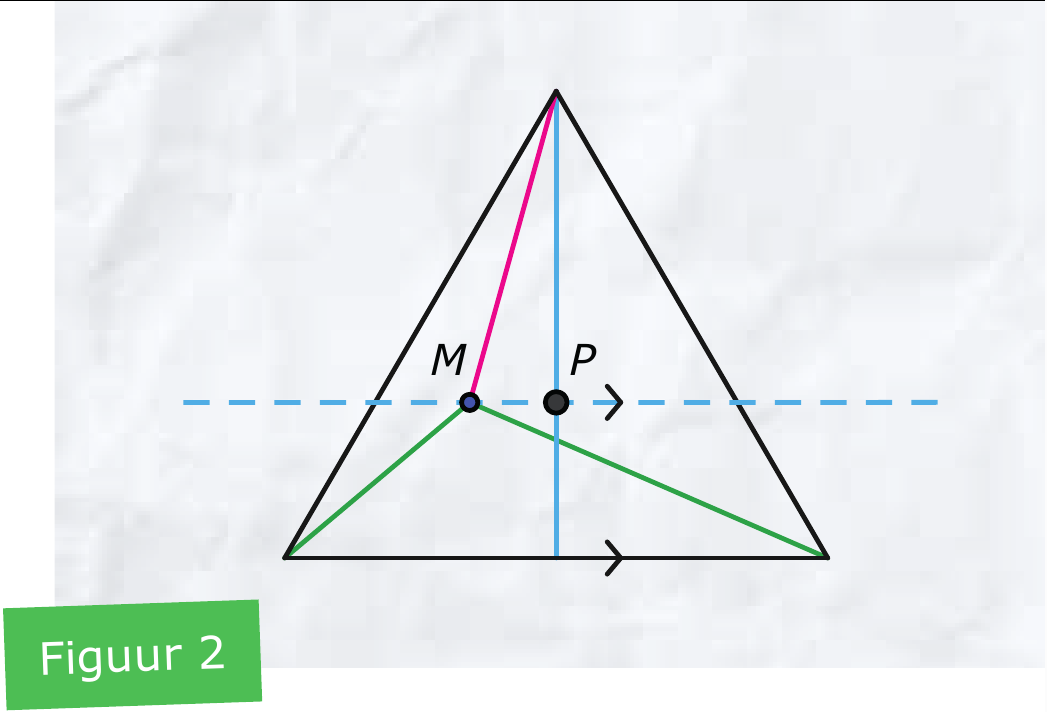
Hoe zit dat bij een zeer symmetrische gelijkzijdige driehoek zoals in figuur 2? Toon aan dat elk punt dat buiten een symmetrielijn valt niet het beste punt zou kunnen zijn. Waarom geeft punt $P$ een kleinere waarde voor $t$ en ook voor $r + s$ dan punt $M$?
Wat overblijft als het allerbeste punt is het snijpunt van de drie symmetrieassen – het onbetwiste middelpunt van de driehoek.
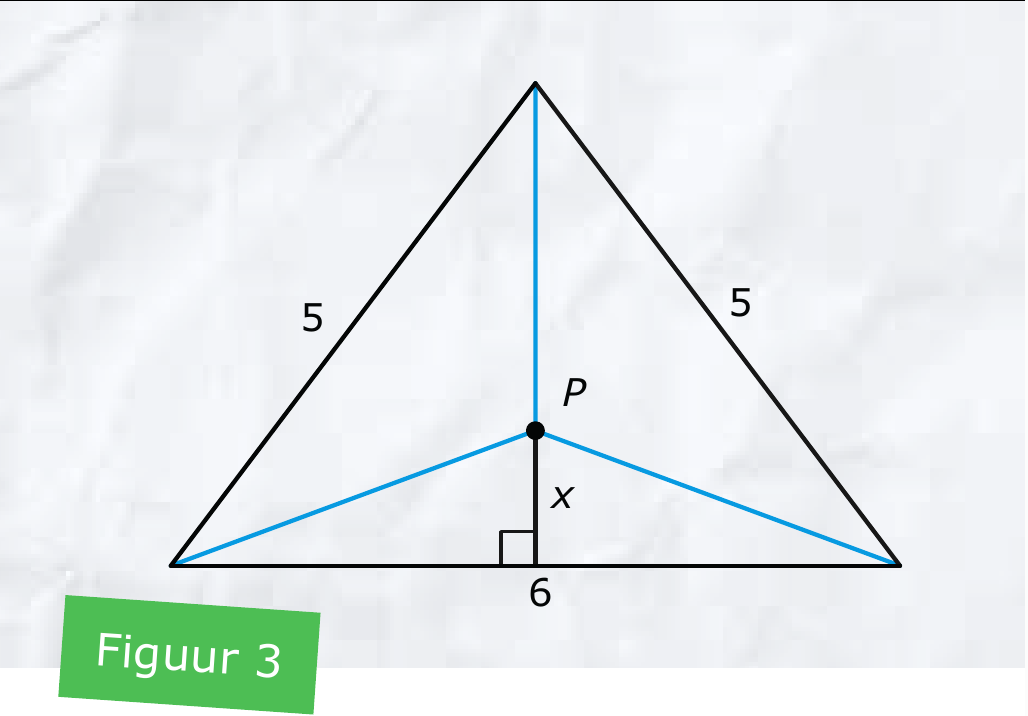Hoe gaat het bij een gelijkbenige driehoek. Hier is er maar één symmetrielijn en symmetrie alleen zal het beste punt niet $B$ kunnen bepalen. Stel je een driehoek met zijden van $5$, $5$ en $6$ voor zoals in figuur 3. Welk punt op de symmetrielijn zou het beste zijn? Noem de afstand tussen het midden van de basis en een variabel punt $P$ op de symmetrielijn $x$. Nu is de totale afstand tussen punt $P$ en de drie hoekpunten van de driehoek een functie van $x$, zeg $f(x)$.
Opgave 4
Gebruik de afgeleide van deze functie om aan te tonen dat het beste punt het punt is waar de drie lijnen naar de hoekpunten van de driehoek gelijke hoeken van $120^o$ maken.
Daar de halve lengtes op de basis en de hoogte allemaal constanten zijn, zou dezelfde uitkomst gelden voor elke gelijkbenige driehoek.
Op een soortgelijke manier kunnen wij aantonen dat er in ieder geval betere punten binnen onze niet-symmetrische $4$-$5$-$6$ driehoek te vinden zijn. Maar welk punt het beste is blijft een heel moeilijke vraag.
Een simpel experiment geeft inzicht. Het strak trekken van het touwtje in figuur 5 geeft een fysieke analoog voor het zoeken naar de kleinste totale afstand. En de verrassende uitkomst is dat ook hier steeds hoeken van $120^o$ ontstaan. Dit blijkt een van de stellingen van Fermat te zijn die eerst bewezen werd door Toricelli, de uitvinder van de barometer Een heel mooi bewijs hiervoor is te vinden in het artikel van Birgit van Dalen en Quintijn Puite in Pythagoras 48-5 (april 2009).
HULPSTELLINGEN
De som van twee zijden van een driehoek is altijd groter dan de derde zijde.
De formule van Heron voor de oppervlakte van een driehoek.
Voor driehoeken geldt:
Oppervlakte $= (a \cdot b \cdot \sin C)/2$.
De afgeleide van $f(x) = \sqrt{k^2+x^2}$ met $k$ een constante is ${x \over \sqrt{k^2+x^2}}$.
De sinusregel.
De cosinusregel.
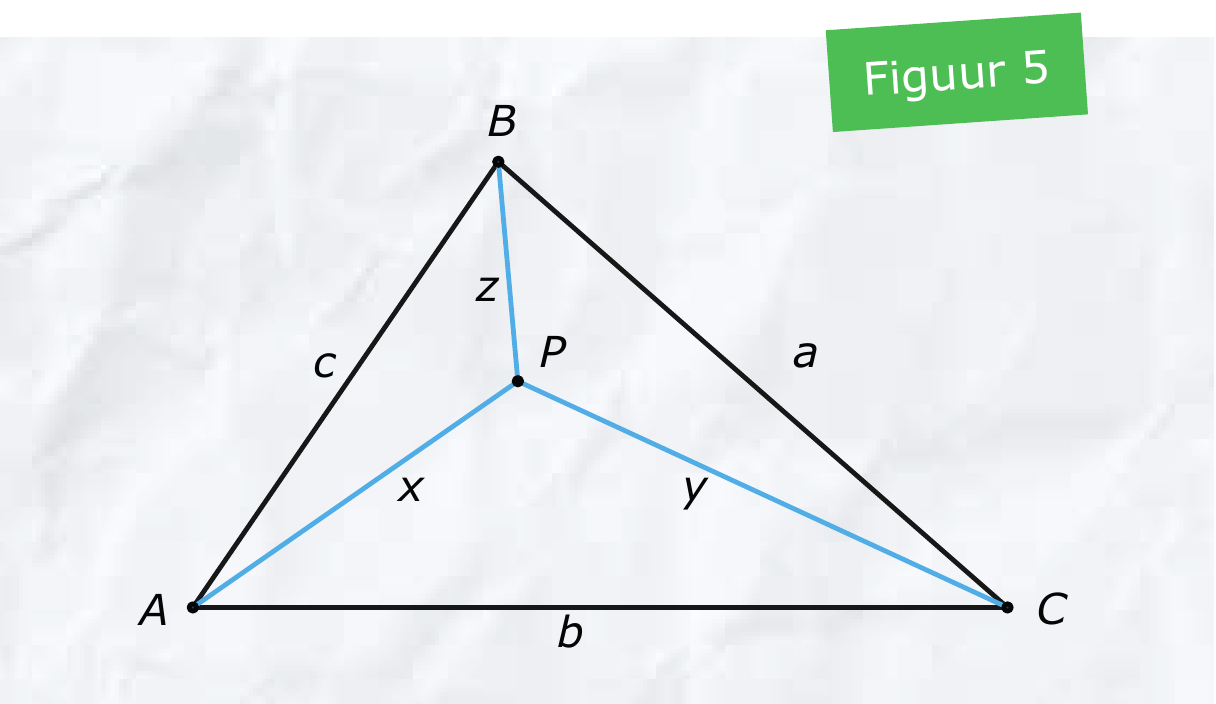Nu kunnen wij de totale kabellengte berekenen en dus de bekabelingskosten bepalen. Dit kan ook met een formule bij zijden $a$, $b$, en $c$ in plaats van $4$, $5$, en $6$. Figuur 5 is een tekening van het gezochte punt $P$ en de lengtes $x$, $y$, en $z$ en in het kader staan alle nodige hulpstellingen. De vier driehoeken in figuur 5 leveren veel vergelijkingen op die verbanden tonen tussen de zes afstanden, $a$, $b$, $c$, $x$, $y$ en $z$. Hierbij is het heel belangrijk dat de drie hoeken van $120^o$ gelijk zijn en makkelijke sinus- en cosinuswaarden hebben.
Opgave 5
Probeer met deze formules een uitdrukking te vinden voor $(x + y + z)^2$ en dus ook voor $(x + y + z)$ in termen van $a$, $b$, en $c$.
Als dat gelukt is kan deze subsidievraag ingeleverd worden.
Nu is het wachten op de ambtelijke molens en dat geeft veel tijd om te denken aan de verdeling van de kosten. In het begin van het proces ging iedereen uit van een gelijke verdeling tussen de drie families, maar het zou ook handig zijn om iedere familie de kosten van zijn verbindingskabel met punt $P$ zelf te laten betalen. Om deze kosten in kaart te brengen moeten wij verder gaan rekenen en de lengtes $x$, $y$, en $z$ bepalen.
En nu verder leven van de wind.
Bekijk oplossing
