OPGAVE 1

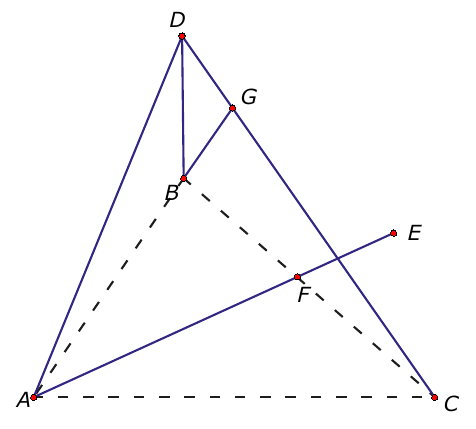
Simpel te bewijzen is dat punt $F$ beter is dan punt $E$. Punt $B$ is ook beter dan punt $D$ want:

\begin{eqnarray*} |AD| + |DG|& >&|AB| + |BG|\\ |BG| + |GC| &>&|BC| \end{eqnarray*}

En dus $|AD| + |DC| > |AB| +|BC|$ en $|AD| + |DB| + |DC| >|AB| + |BC|$

 

OPGAVE 2

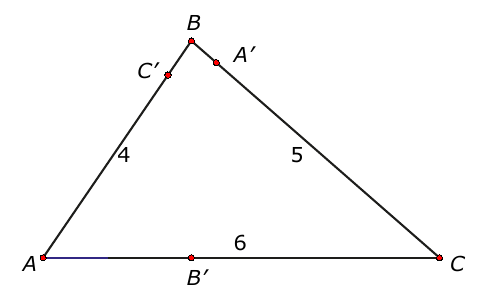
De beste drie punten zijn de drie snijpunten ($A’$, $B’$ en $C’$) van de hoogtelijnen met de zijden van driehoek $ABC$ en met de formule van Heron is $C’$ de allerbeste.

 

OPGAVE 3

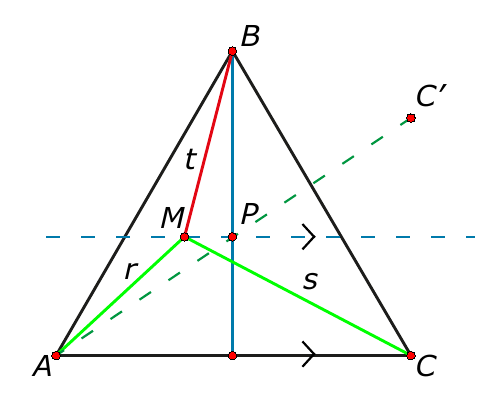
In driehoek $MBP$ is de zijde $BP$ korter dan de schuine zijde $MB$. Het punt $C’$ is het spiegelbeeld van punt $C$ in de lijn door $M$ en $P$ en $|AP| + |PC’| < |AM| + |MC’| = |AM| + |MC|$.

 

OPGAVE 4

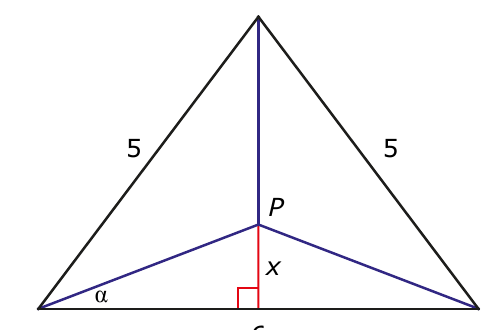
$f (x) = 4 - x + 2 \sqrt{9 + x^2}$ en $f (x ) = -1 + {2x \over \sqrt{9+x^2}}$.

Als je $\sin(α)$ in deze formule herkent dan is het duidelijk dat $f(x)$ een minimumwaarde heeft als $α = 30^o$. Dit betekent dat er bij het gezochte punt $P$ drie hoeken van $120^o$ ontstaan.

 

OPGAVE 5

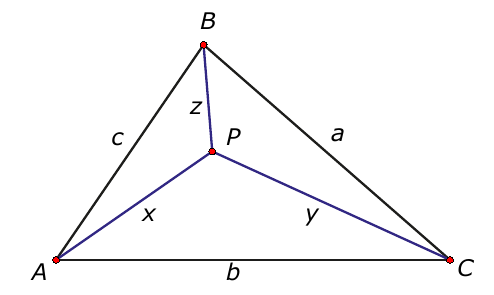
Met de cosinusregel kun je aantonen dat

\begin{eqnarray*} a^2 &=& y^2 + z^2 + yz\\ b^2 &=& x^2 + y^2 + xy\\ c^2 &=& x^2 + z^2 + xz \end{eqnarray*}

Met Heron en de oppervlakteformule volgt dat:

$$xy \cdot {\sqrt{3} \over 4} + xz \cdot {\sqrt{3} \over 4} + yz \cdot {\sqrt{3} \over 4} = \sqrt{s(s-a)(s-b)(s-c)}$$

en dus $xy + xz + yz = 4 \cdot \sqrt{s (s - a) (s - b) (s - c)} / \sqrt{3}$ waar $s = {a + b + c \over 2}$.

Er geldt bovendien dat $(x + y + z)^2 = x^2 + y^2 + z^2 + 2xy + 2xz + 2yz$, dus volgt uit bovenstaande formules dat:

$$(x + y + z)^2 = {a^2+b^2+c^2 \over 2} + {3 \over 2} \cdot {4 \over \sqrt{3}} \cdot \sqrt{s (s - a) (s - b) (s – c)}$$

en dus

$$(x + y + z) = \sqrt{{a^2+b^2+c^2 \over 2} + 2 \sqrt{3 s (s - a) (s - b) (s – c)}}.$$

Laten we dit $M$ noemen.

Dan is $a^2 – b^2 = z^2 – x^2 + yz – xy = (z – x)(z + x) + y(z – x)=(x+y+z)(z-x)$. Dus $a^2 – b^2 = M \cdot (z – x)$ en $z-x = {a^2-b^2 \over M}$.

Op dezelfde manier is $z - y = {c^2-b^2 \over M}$.

Dit geeft $z = (M + {a^2-b^2 \over M} + {c^2-b^2 \over M})/3$.

In het concrete geval van de drie dorpen zijn de afstanden respectievelijk, $2{,}924$ km, $3{,}978$ km, en $1{,}635$ km.