Nog $27$ jaar, en dan is het 2048. Dat is niet zomaar een jaartal, nee het is een macht van twee, en in onze digitale wereld draait eigenlijk alles om machten van twee. Waarom zitten we nog steeds vast aan ons tientallige stelsel, terwijl er zoveel efficiënter gebruik gemaakt kan worden van een zestientallig stelsel? Hieronder volgt een
introductie. 

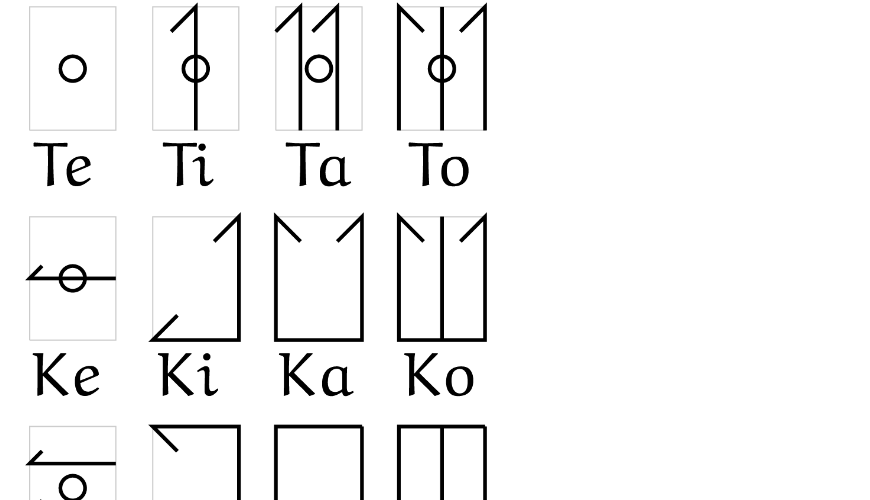
Om te beginnen moet je opnieuw leren tellen. Eerst tellen we tot $15$. Dat gaat als volgt: $0$ wordt $Te$, $1$ wordt $Ti$, $2$ wordt $Ta$, $3$ wordt $To$. Nu schakelen we over op een andere medeklinker, de $K$. $4$ wordt $Ke$, $5$ wordt $Ki$, $6$ wordt $Ka$, $7$ wordt $Ko$ en opnieuw schakelen we over op een andere medeklinker, de $F$. We hebben $8$ is $Fe$, $9$ is $Fi$, $10$ is $Fa$ en $11$ is $Fo$. 

De laatste $4$ getallen zijn met de $P$: $12$ is $Pe$, $13$ is $Pi$, $14$ is $Pa$ en $15$ is $Po$. Dus we hebben $Te, Ti, Ta, To, Ke, Ki, Ka, Ko, Fe, Fi, Fa, Fo,
Pe, Pi, Pa, Po$.

En nu $16$, heel simpel: waar $Ti$ $1$ is gebruiken we $Tri$ voor $16$. En dat geldt heel algemeen: als je een $R$ plaatst tussen de medeklinker en de klinker dan verhoog je het getal naar $16$ tot de macht het oorspronkelijke getal. Dus $Tri$ staat voor $16$, $Tra$ staat voor $256$,$Tro$ staat voor $4096$, $Kre$ staat voor $65536$, enzovoort tot $Pro$ dat staat voor $1\ 152\ 921\ 504\ 606\ 846\ 976$. Dat is het equivalent van een triljoen. 

Je wilt natuurlijk ook getallen op papier kunnen zetten. Daar heb ik ook over nagedacht. Basaal staat een $|$ voor $1$ en $-$ voor $4$. Door meerdere streepjes te combineren kom je uit op de getallen $1$ tot en met $15$. De $0$ wordt een klein cirkeltje. Dat wordt ook elders gebruikt om het "ontbreken" aan te geven. 

Je ziet ze hieronder staan.

Laten we maar meteen nadenken over het grootschalig toepassen van het $Tri$-tallig stelsel. Bijvoorbeeld muntstukken zullen geslagen worden van $1$, $2$, $4$, en $8$ eurotriques waarbij $16$ eurotriques samen een euro zijn. De munten van $1$ en $2$ euro blijven gespaard, maar mogelijk komt er ook een munt van $4$ euro. Dan volgen biljetten van $8$, $16$, $32$, $64$ euro. 

Een byte is $8$ bits. Een kilobyte (kb) is eigenlijk $1024$ bytes, oftewel precies een $KeTra$-byte. 1 Mb is een $Kri$-byte. Dan volgt 1 Gb oftewel een $KeKro$-byte. Een Tb is vervolgens een $Fra$ en daarna volgen nog Pb (Peta-byte): een $KePre$. Ten tenslotte is de Eb (Exabyte) een $Pro$.

Het vieren van lustrums elke $5$ jaar zal volledig achterhaald zijn. Dat wordt $4$ jaar. Het vieren van $25$ jaar? Nee, dat wordt $32$ jaar, het $TaTri$-feest. Groot feest bij $KeTri$ jaar. En zeker $FeTra$ gaat heel groot gevierd worden. We moeten wel uitkijken met de zogenaamde $FeTra$-bug.

Getalsmatig gaan er ook dingen veranderen. Deelbaarheidskenmerken van $5$ zijn niet meer zo eenvoudig als tot nog toe. Daarvoor in de plaats moet je kijken naar de som van de cijfers van het getal, net zoals we nu doen met het deelbaarheidskenmerk van $3$.