De rij van Fibonacci is één van de beroemdste getallenrijen uit de wiskunde. Zij is genoemd naar de Italiaanse wiskundige Leonardo van Pisa, bijgenaamd Fibonacci, die leefde van 1170 tot ca. 1250. Deze rij komt voor in zijn boek Liber Abaci uit 1202. De eerste twee getallen in de rij van Fibonacci zijn $0$ en $1$. Elk volgend getal in de rij is de som van de twee voorgaande. Dat levert dus 

$$0, 1, 1, 2, 3, 5, 8, 13, 21, \ldots$$

In het algemeen geldt voor de ne term $T_n$ in de rij:

$$T_n = T_{n-2} + T_{n-1}$$

Net als Roland de Jong Orlando hebben veel kunstenaars de rij van Fibonacci op een of andere manier in hun werken en sculpturen verwerkt.

De modules

Het werk van Ronald de Jong Orlando is opgebouwd uit twee soorten blokjes, of modules. Voor die modules is uitgegaan van een balk met een vierkante dwarsdoorsnede. Eerst wordt die onder een hoek van $30^{\rm o}$ met de dwarsdoorsnede doorgezaagd (figuur 1). Vervolgens wordt het linkerdeel uit figuur 1 over $90^{\rm o}$ van je af gekanteld en opnieuw onder een hoek van $30^{\rm o}$ met de dwarsdoorsnede doorgezaagd (figuur 2). Dat levert een blokje met aan twee kanten een rechthoekig zijvlak, de oorspronkelijke zaagvlakken. Deze zijn even groot maar anders georiënteerd.

Vervolgens wordt het rechterdeel uit figuur 1 over $90^{\rm o}$ naar je toe gekanteld en opnieuw doorgezaagd onder een hoek van $30^{\rm o}$ met de vierkante dwarsdoorsnede, maar nu in tegengestelde richting. Het resultaat is dan weer een blokje met aan twee kanten een rechthoekig zijvlak, de oorspronkelijke zaagsneden. Ook deze zijn even groot maar anders georiënteerd. In figuur 3 is het hele proces nog eens weergegeven.

De eerste zaagsnede onder een hoek van $30^{\rm o}$ (boven). Dan linkerdeel over $90^{\rm o}$ draaien (hier naar boven) en rechterdeel  over $90^{\rm o}$ draaien (hier naar beneden).  Daarna beide delen langs de aangegeven lijn doorzagen.

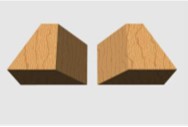
De beide blokjes (zie figuur 4) lijken veel op elkaar maar zijn niet hetzelfde. Ze zijn elkaars spiegelbeeld. Voor het onderscheid is het ene kort aangegeven met L (links) en
het andere met R (rechts). Omdat alle zaagvlakken bij beide blokjes even grote rechthoeken zijn kunnen de blokjes daar precies aansluitend aan elkaar worden gezet. Zo zijn in figuur 5 twee R-modules en in figuur 6 een L- en een R-module aan elkaar gezet.

L- en R-module	Twee R-modules aan elkaar	L- en R-module aan elkaar

Ritmo Fibonacci

Al in 2006 maakte Roland de Jong Orlando gebruik van de rij van Fibonacci bij het aan elkaar bevestigen van de beschreven modules. Hij gebruikte toen alleen maar R-modules en zette die achtereenvolgens aan elkaar als termen in de rij. Dus eerst 1R (0R heeft uiteraard geen zin!), dan weer 1R, dan 2R, enzovoorts. Zo kreeg hij dus de rij:

$$1R, 1R, 2R, 3R, 5R, 8R, 13R$$

In Ritmo Fibonacci is dat van onder naar boven weergegeven (figuur 7).

Ritmo Fibonacci (2006)

Afwisselend

Bij de Fibonacci Swing was de werkwijze min of meer vergelijkbaar. Daar werden afwisselend R- en L-modules gebruikt. De Fibonaccitermen werden echter niet stuk voor stuk afzonderlijk getoond, maar aan elkaar vastgemaakt. Zo is het rechterdeel van deFibonacci Swing als volgt opgebouwd: 1R, 1L, 2R, 3L, 5R en tenslotte 8L. In de onderdelen van figuur 8 is dat stap voor stap weergegeven. Het linkerdeel is daar het spiegelbeeld van. Dat wordt dan 1L, 1R, 2L, 3R, 5L en 8R. Ten slotte zijn linker- en rechterdeel aan elkaar vastgemaakt en is het geheel op een sokkel geplaatst.

Stapsgewijze opbouw van de Fibonacci Swing

Kokers in plaats van blokjes 

Voor de Fibonacci Swing zijn in totaal 20 L- en 20 R-modules nodig. Die zouden stuk voor stuk op de aangegeven manier uit een houten balk met een vierkante dwarsdoorsnede kunnen worden gezaagd. Daarna kunnen ze op de aangegeven wijze bij de zaagvlakken aan elkaar worden bevestigd.

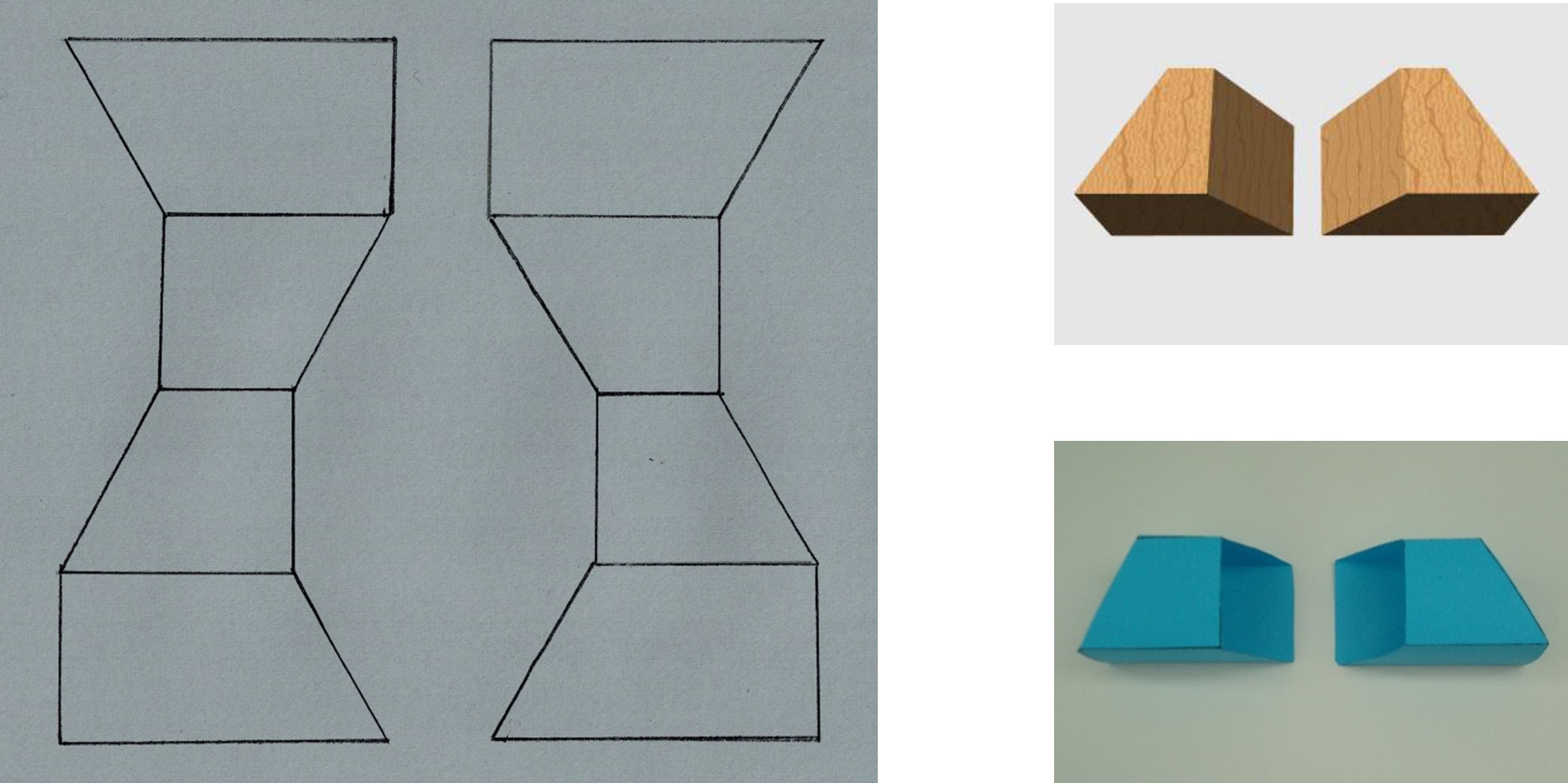
De Fibonacci Swing is echter niet van (massief) hout, maar van Cortenstaal. Daar zijn de modules geen massieve blokjes maar holle metalen kokers, immers de vlakken waar deze kokers aan elkaar worden gezet kunnen achterwege blijven. In figuur 9 staan voorbeelden van de uitslag van zo’n L-koker en R-koker. In feite werd in figuur 3 al gewerkt met een holle kokervormige balk! De kokers hebben bij de Fibonacci Swing een vierkante doorsnede van $103 \times 103$ mm en hun maximale lengte is 150 mm. Met het gegeven dat de 'zaaghoek' steeds $30^{\rm o}$ is, liggen alle afmetingen van deze kokers vast.

Uitslagen van een L-module (links) en een R-module (rechts) met "zaaghoeken" van $30^{\rm o}$. Ter vergelijking nog de beide blokjes (linksonder) en de beide kokers (rechtsonder)