Tijdens een bezoek aan de kathedraal van Lipari en het bijbehorende klooster kreeg ik opeens van leerlingen de vraag hoe de kruisgewelven daar in elkaar zaten. Die in de kathedraal hadden prachtige fresco's en waren puntig, wat de uitleg iets lastiger maakte. Maar de oude Romaanse gewelven in de kloostergang, gebouwd rond 1130, bestonden uit eenvoudige, elkaar kruisende cilinders en waren bovendien vrij laag zodat je de structuur goed kon zien.

Figuur 1A: klassiek tongewelf in een oude kelder	Figuur 1B: gewelf met ellipsvormige dwardoorsnede in het voormalig Hoofdpostkantoor, nu de bibliotheek in Utrecht (foto: Isabelle Cornet)

De eenvoudigste gewelven zijn zogeheten tongewelven. Een klassiek tongewelf bestaat uit een gemetselde halve cilinder. Kelders onder oude panden in steden als Utrecht, Delft, Brugge en Gent, maar ook onder monumentale boerderijen, hebben vaak deze structuur. Er zijn ook kerken met oude, houten tongewelven, zoals de Sint Amanduskerk in Roeselare, de Janskerk in Utrecht en de Grote of Sint-Vitus Kerk in Naarden met zijn indrukwekkende, beschilderde tongewelf. De dwarsdoorsnede van een tongewelf kan ook een andere vorm hebben, zoals een ellips of een parabool of een combinatie van twee cirkelbogen.

Figuur 2A: Grote Kerk te Naarden	Figuur 2B: Kathedraal San Bartolomeo op Lipari

Een gewelf moet de krachten opvangen die door zijn eigen gewicht worden veroorzaakt. Als het overal van gelijke dikte is, blijkt het ideale tongewelf als doorsnede precies dezelfde vorm te hebben als een omgekeerde hangende ketting. De kettinglijn is een grafiek van de vorm $y=\tfrac{a}{2}\left(e^{x/a}+e^{-x/a}\right)$ waarin $a > 0$ een parameter is. Een stevige boog moet dus een versie van deze grafiek 'op de kop' volgen, ofwel een kettinglijn met $a < 0$.

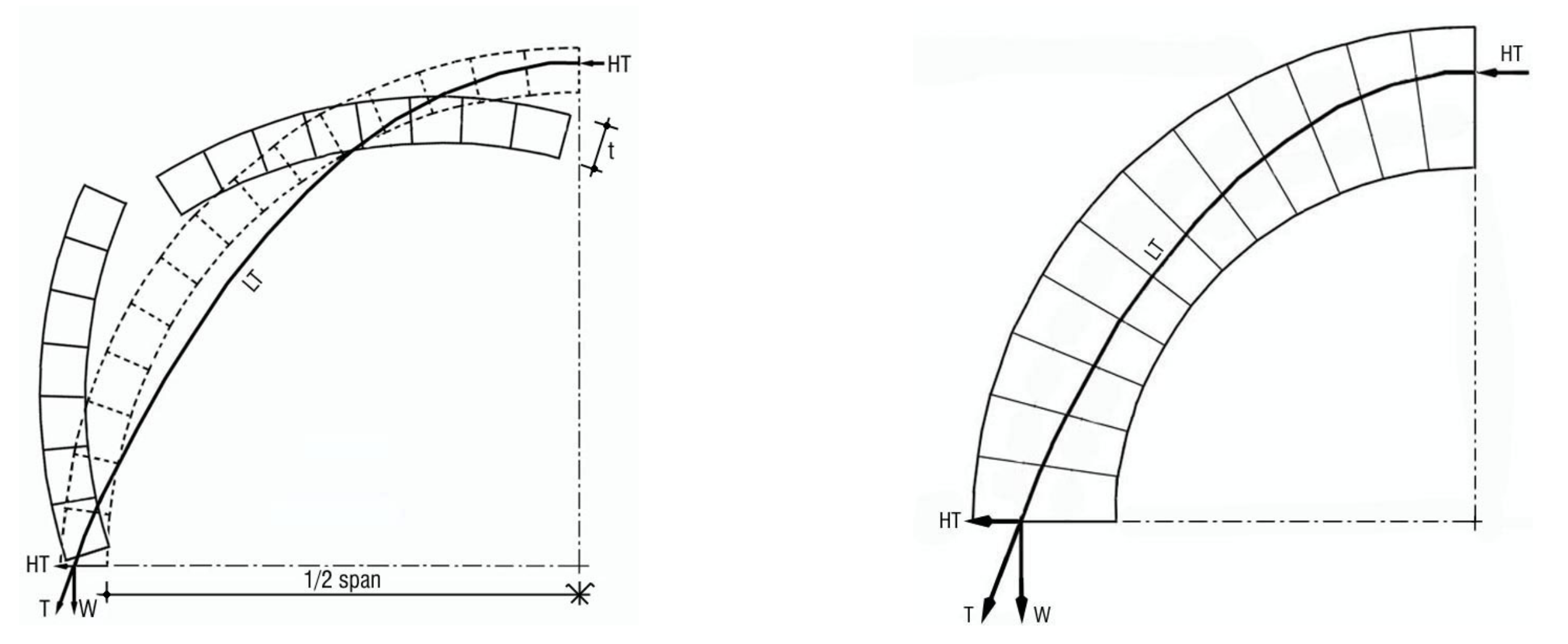
Stel dat een gemetselde boog geen kettinglijn volgt, maar dat deze ideale lijn van de top tot de voetpunten onder de overkapping ligt zoals linksboven in figuur 3. De trek- en duwkrachten als gevolg van het eigen gewicht van de boog duwen de stenen in dit geval niet tegen elkaar, maar trekken de top naar de voetpunten toe. Hierdoor kan de boog instorten. Rechtsboven in figuur 3 is een cilindervormige boog getekend, die gebouwd is met dikkere stenen, zodanig dat er wèl een kettinglijn is die door alle stenen loopt. De krachten binnenin de gemetselde structuur zijn gericht langs de raaklijn aan deze kettinglijn en duwen de stenen van deze boog dus wel tegen elkaar. De structuur blijft hierdoor staan.

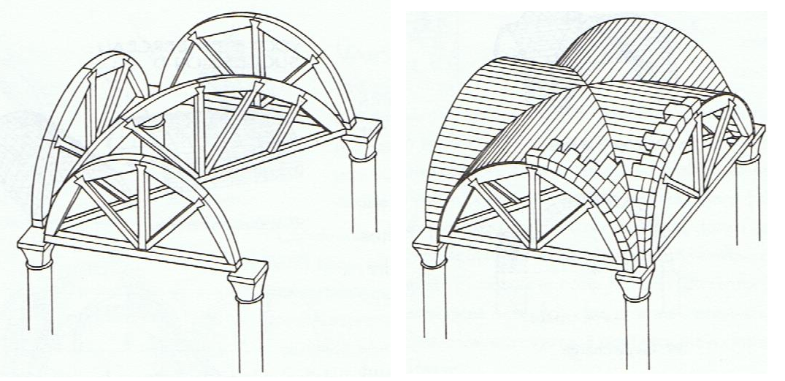
Figuur 3 Spankrachten in een boog volgen een omgekeerde kettinglijn. Als die niet in de boogmuren valt bestaat het gevaar op instorten.

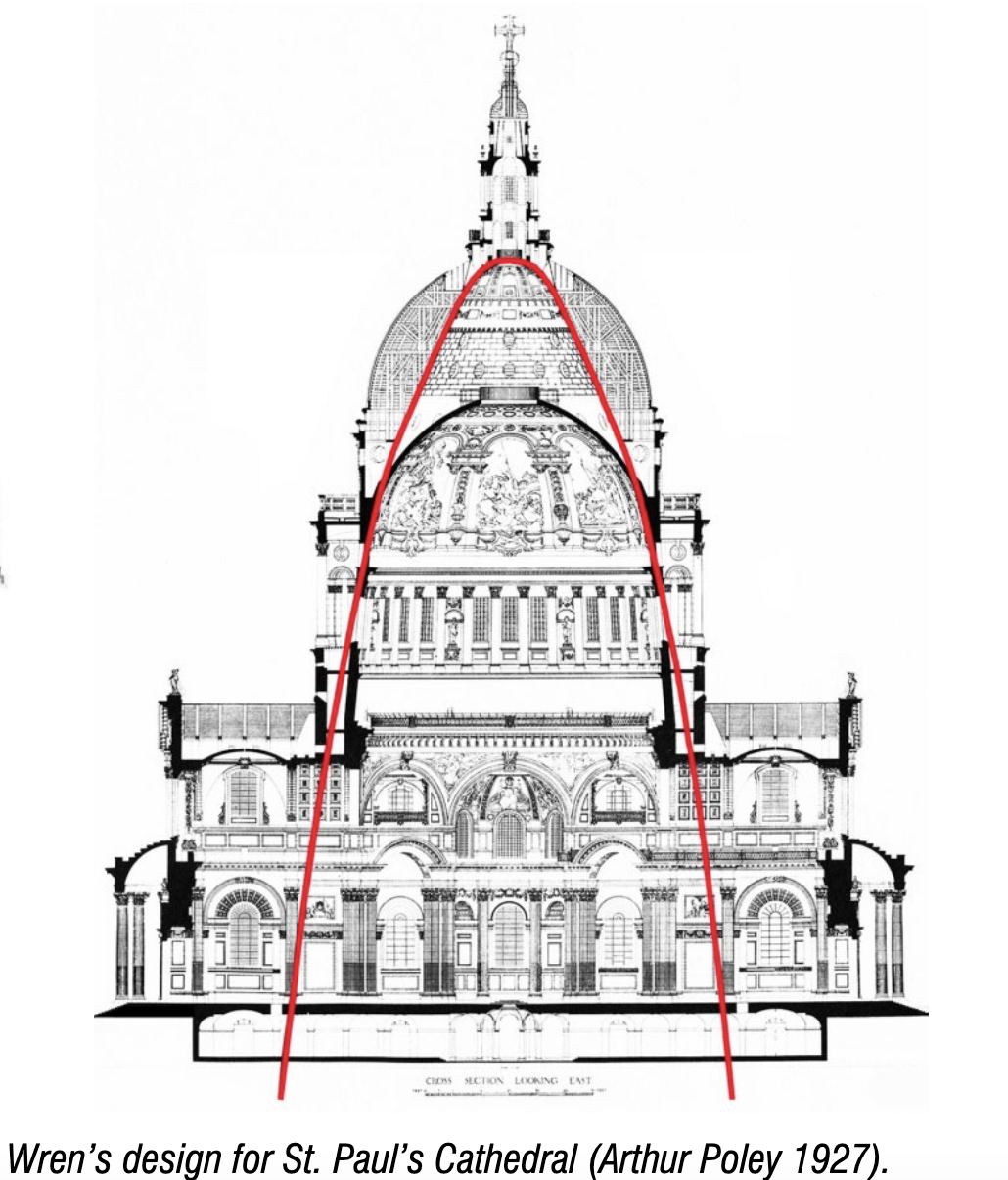
Vooral voor gewelven bovenop hogere verticale muren is er in de praktijk een instortrisico, omdat het geheel van muren en gewelf dan totaal geen kettinglijn volgt. Hierdoor is het risico groot dat de muren uiteen geduwd worden. Met zijbeuken of steunberen aan de buitenmuren kun je zorgen dat de ideale lijn niet meer buiten de gemetselde structuur valt, waardoor het geheel stabiel wordt. In figuur 3 zien we een tekening van St. Paul's Cathedral die illustreert hoe de zijbeuken zorgen voor een totaalstructuur waarbinnen een geschikte kettinglijn valt.

Tongewelven die alleen bestaan uit een halve cilinder bovenop verticale muren hebben vaak trekstangen die instorten voorkomen. Op de foto van de Grote Kerk in Naarden zie je links en rechts onderaan trekstangen, en verstevigende dwarsbalken onder het hoogste tongewelf.

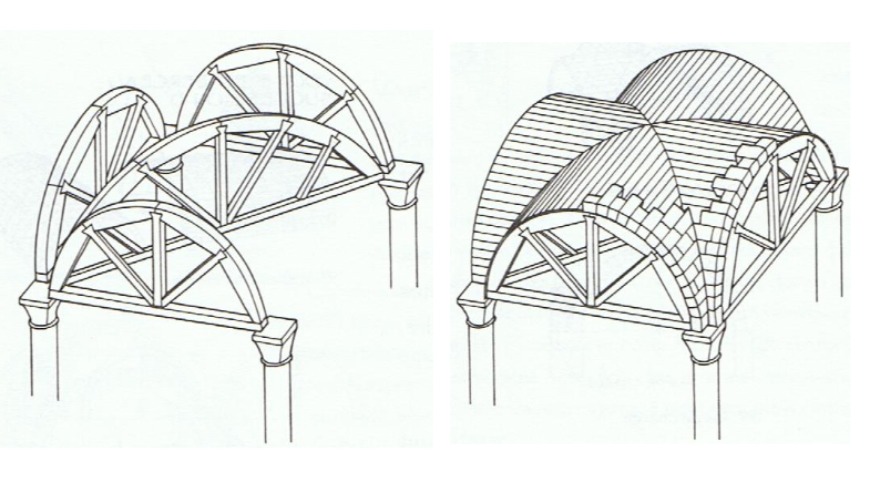
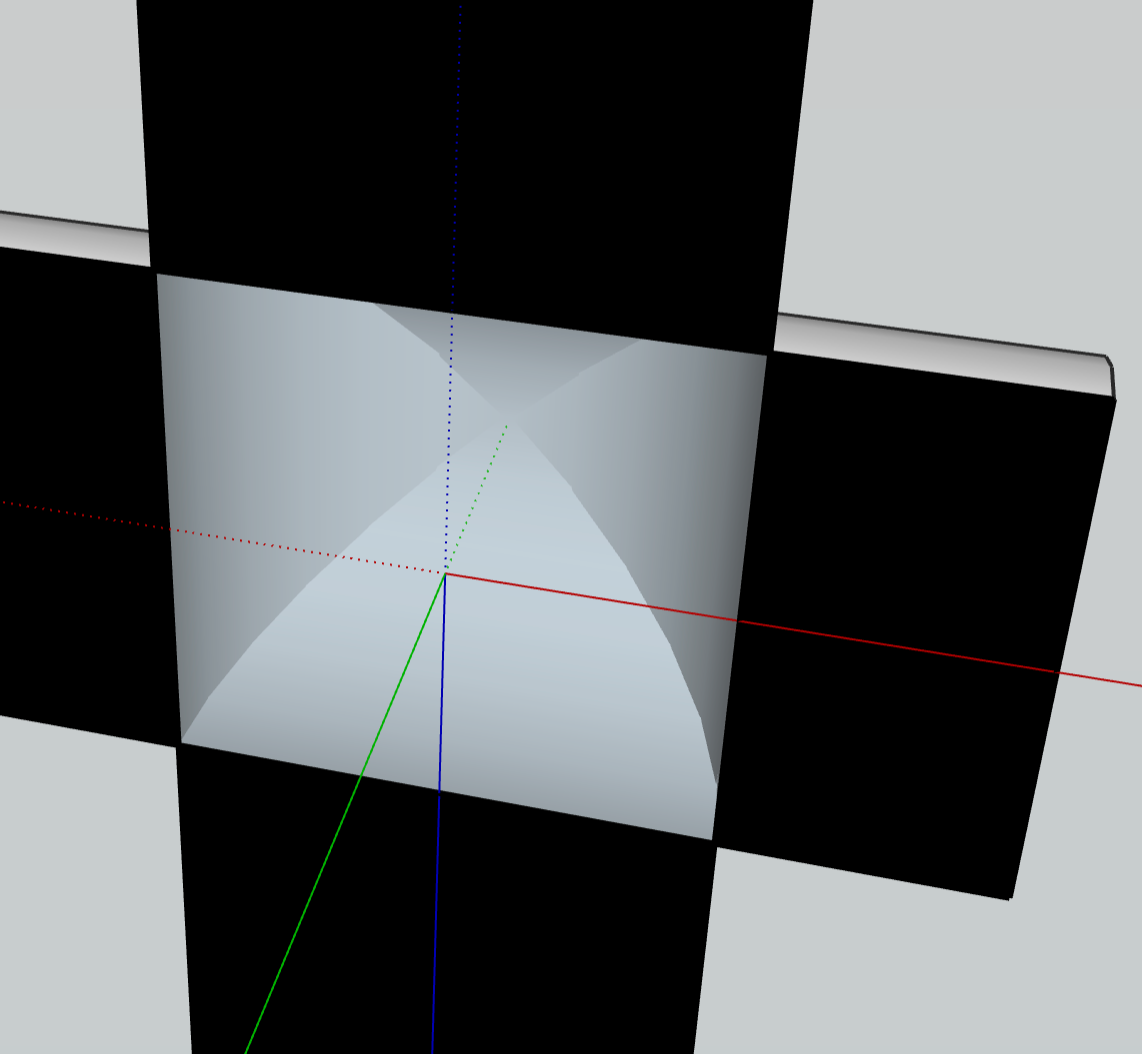
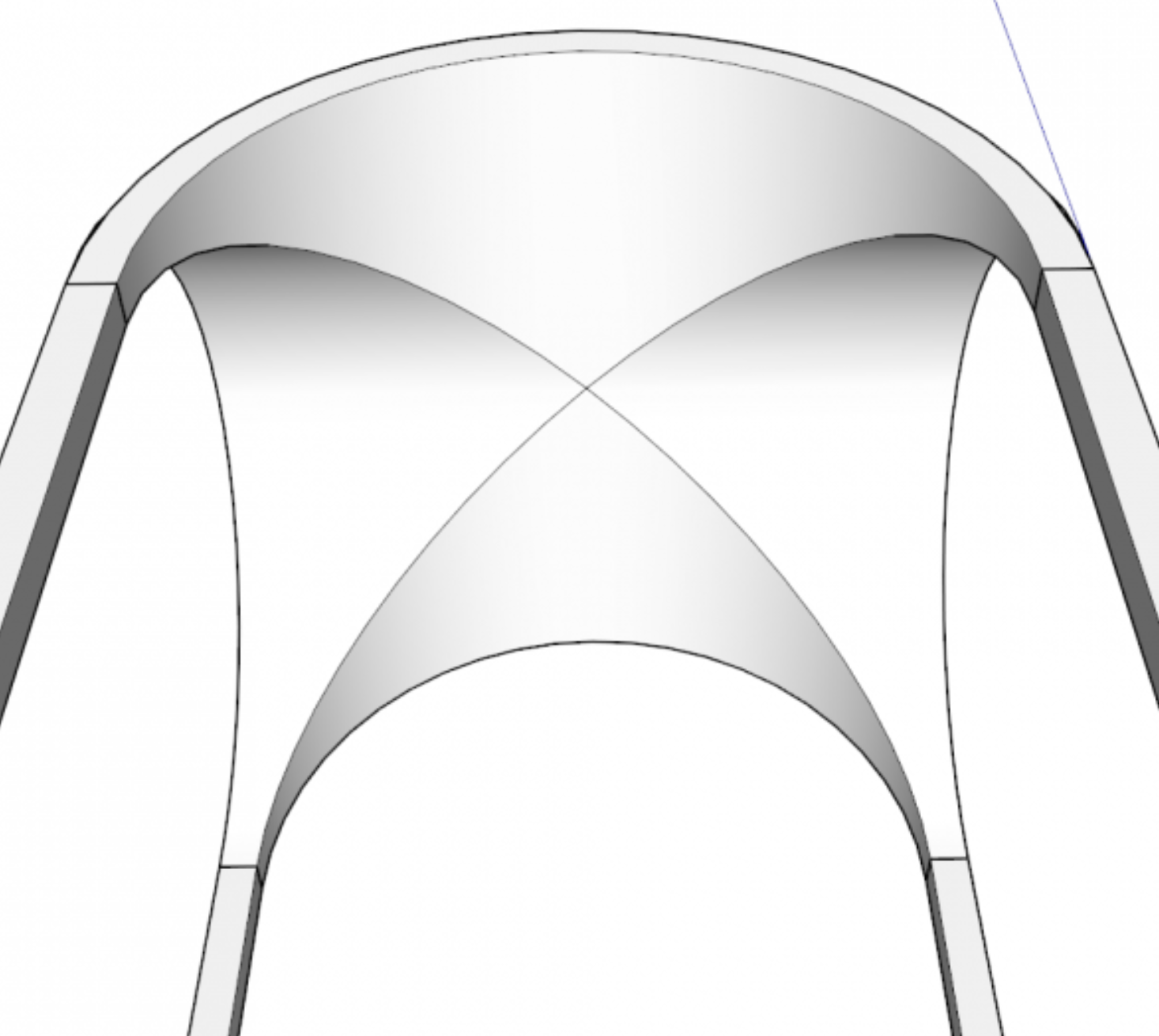
Kruisgewelven en de daarop gebaseerde kruisribgewelven zijn sterker dan tongewelven, waardoor het minder belangrijk is dat het gewelf precies een kettinglijn volgt. Later gebouwde kerken en kelders hebben dan ook vaak kruisgewelven zoals in figuur 4. De te verwachten krachten zijn voor kruisgewelven, net als voor tongewelven, doorslaggevend voor het ontwerp.

Figuur 4: Kloostergang met kruisgewelf in Maagdenburg

Hier zijn vuistregels voor, maar hoe kun je je als architect een voorstelling maken van zo'n gewelf? En hoe bereid je als bouwer de vorm van een te bouwen gewelf voor?

Cilinders snijden

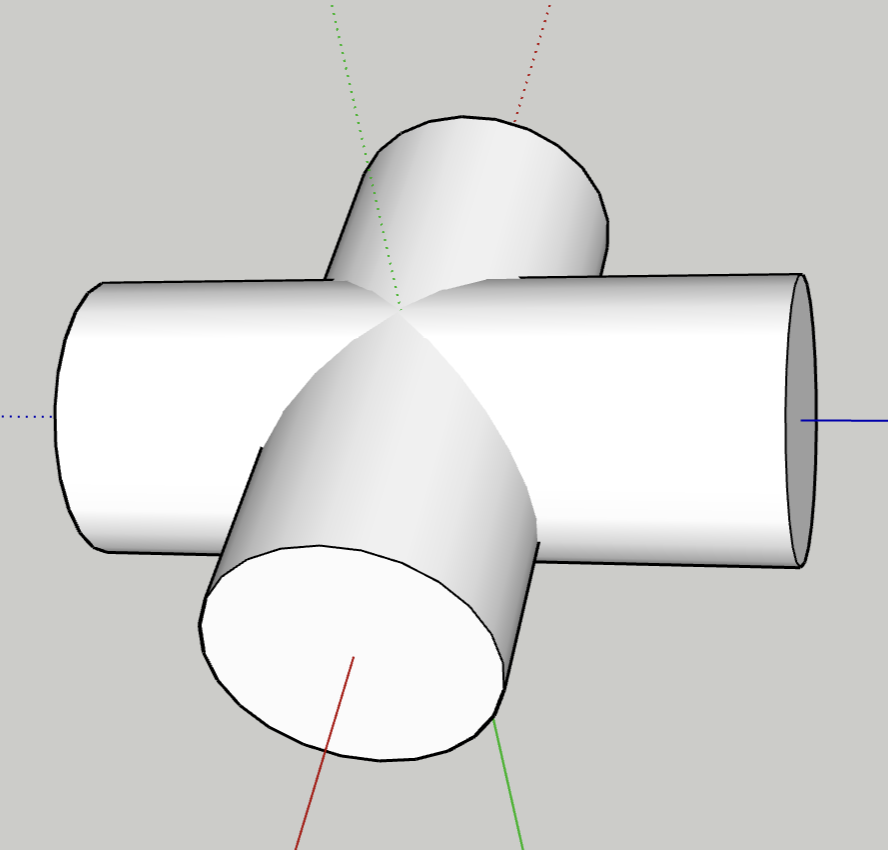
Tegenwoordig kun je met behulp van een tekenprogramma zoals Sketchup of Tinkercad met een beetje oefening vrij eenvoudig cilinders creëren en snijden. De standaardcilinders die je daarin bouwt zijn massief. Een voorbeeld zie je in de Sketchup constructies in figuur 5.

Figuur 5A: haaks op elkaar staande, snijdende cilinders	Figuur 5B: twee elkaar snijdende halve cilinders, waarvan het overlappende deel is weggehaald. De ontstane holte is een kloostergewelf.	Figuur 5C: het resulterende kruisgewelf

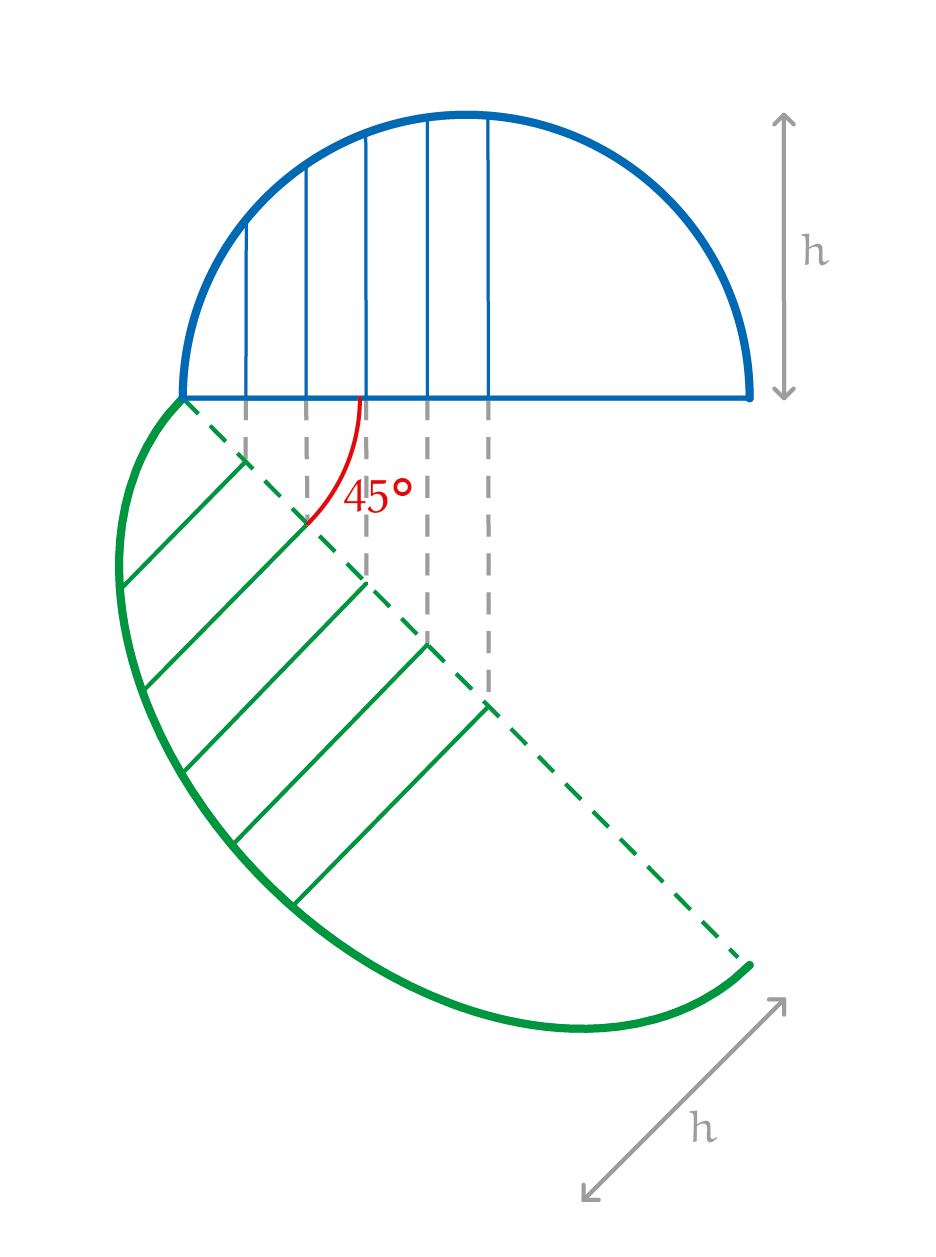
Figuur 5 toont twee cilinders van gelijke doorsnede waarvan de assen elkaar haaks snijden. Als je beide cilinders overlangs halveert en vervolgens het overlappende deel weghaalt, krijg je een uitgeholde structuur. De holte is een zogenaamd kloostergewelf. Uithollen van de massieve delen levert ten slotte het correcte binnenaanzicht van een kruisgewelf op. Op pyth.eu vind je hiervoor linkjes naar een mooie Geogebra applet. Een gemetselde kerk of keldergewelf bouwde men natuurlijk niet door op deze manier cilinders te kruisen, maar op basis van mallen. Als het gewelf een perfecte cilindervorm heeft, wordt de dwarsdoorsnede met behulp van halve-cirkelmallen gemaakt en de diagonalen (die het 'kruis' vormen) met behulp van een bijpassende ellips. Deze mallen kunnen liggend op de grond gemaakt worden, en de ellips kun je dan baseren op de halve cirkel door verticale afstanden te transleren en roteren zodat ze de juiste afstanden opleveren tot een lijnstuk dat een hoek van $45^{\rm o}$ maakt met de cirkeldiagonaal en dat de lange as van de ellips gaat vormen. De halve korte as vormt de hoogte $h$ van de ellipsboog en is gelijk aan de straal van de cirkelboog. De lange as van de ellips is gelijk aan $2\sqrt{2}h$, ofwel $\sqrt{2}$ maal de diameter van de cirkelboog. Zie figuur 6.

Figuur 6A: Metselen op een frame gebaseerd op houten cirkel- en ellipsbogen	Figuur 6B: uitlijnen van de ellipsboog op de grond

Een ellips werd in de vierde eeuw voor Christus gedefinieerd als een doorsnijding van een kegel met een plat vlak, maar in deze context wordt het diagonalen-kruis bepaald door het doorsnijden onder een hoek van $45^{\rm o}$ van een cilinder met een plat vlak. Dat dit ook een ellips oplevert kan op verschillende manieren bewezen worden. Een moderne beschrijving is dat een ellips een uitgerekte cirkel is, en die beschrijving komt duidelijk overeen met de constructie van de bogen in figuur 6. Als de
halve cirkel in een coördinatenstelsel wordt gegeven door de formule $y = \sqrt{h^2 - x^2}$, of equivalent, door de parametervoorstelling $\left(x(t),y(t)\right) = \left(h\cos(t),h\sin(t)\right)$ voor $0 \le t \le \pi$, dan kan een ellips van de juiste afmetingen worden verkregen door een horizontale vermenigvuldiging met factor $\sqrt{2}$. De halve ellips is dan gelijk aan $y = \sqrt{h^2 - x^2/2}$ ofwel $\left(x(t),y(t)\right) = \left(h \sqrt{2} \cos(t),h\sin(t)\right)$ voor $0 \le t \le \pi$.

Knutselen met Cilinders

Om een gevoel te krijgen voor het samenspel van cilinders die de gewelven vormen kun je natuurlijk ook met keukenrollen aan de slag gaan. Of je kunt een uitslag maken van de delen van de cilinders die het gewelf vormen. Daarvoor is het nodig om te weten hoe de snijcurve van de twee cilinders eruit ziet. We zoeken dat hier uit in een driedimensionaal coördinatenstelsel. Daarin kun je een cilinder beschrijven met de formule die in twee dimensies een cirkel voorstelt: een cirkel met straal $1$ rond de oorsprong wordt gegeven door de vergelijking $x^2 + y^2 = 1$. Omdat deze vergelijking niet van $z$ afhangt, geeft hij op iedere hoogte $z$ een cirkel. En deze 'stapel' cirkels is precies een cilinder rond de $z$-as.

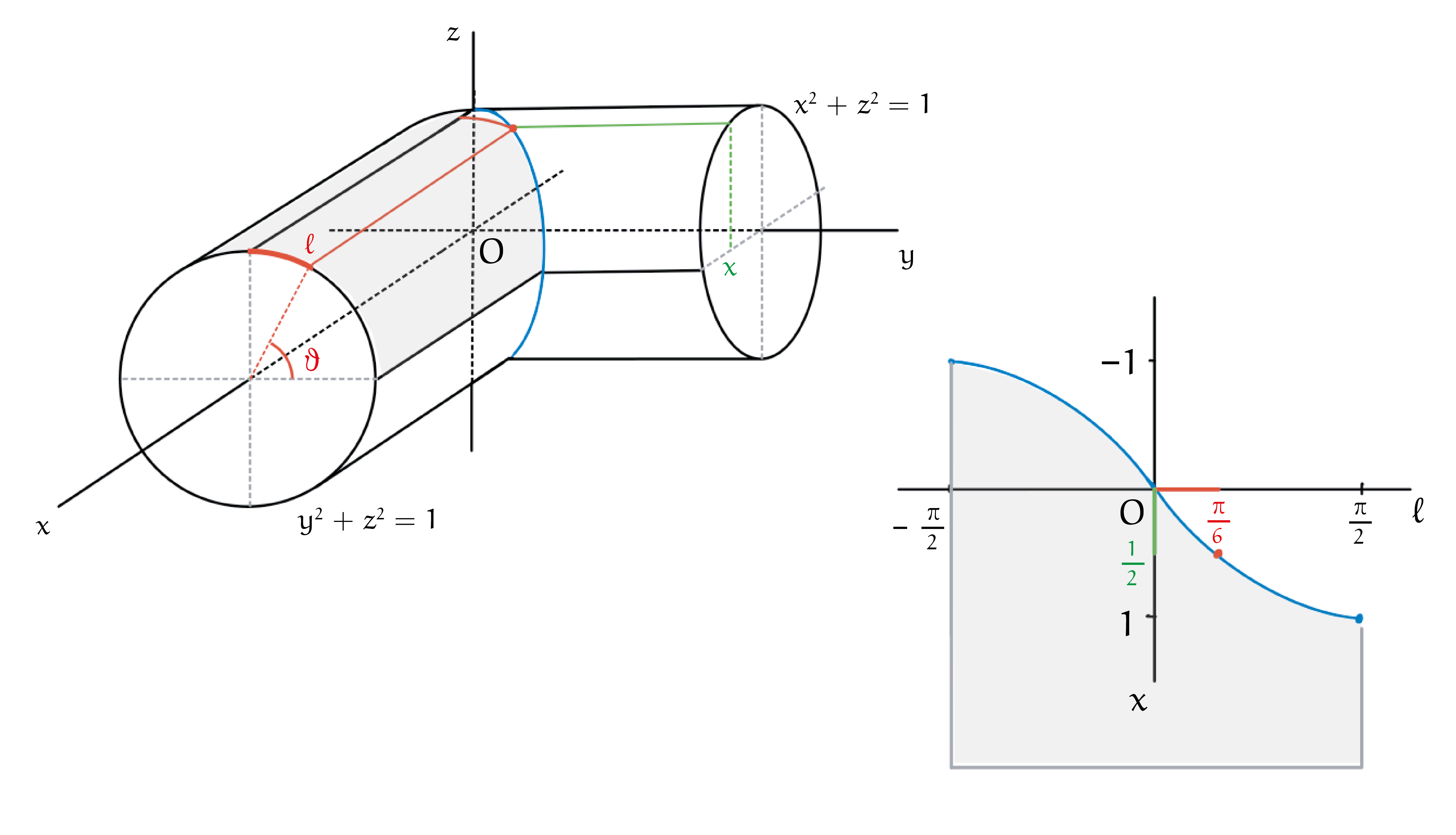Figuur 7: De cilinders snijden elkaar in de blauwe curve, die in het vlak $x = y$ ligt. In de uitslag van de cilinder $y^2 + z^2 = 1$ is het punt $(\ell,x) = (\tfrac{\pi}{6}, \tfrac{1}{2})$, op de snijcurve aangegeven.

In figuur 7 zijn twee cilinders met straal $1$ afgebeeld waarvan de centrale assen beide door de oorsprong gaan. De ene heeft de $x$-as als centrale as en wordt gegeven door $y^2 + z^2 = 1$, de andere ligt rond de $y$-as en voldoet aan $x^2 + z^2 = 1$. De holle cilinders snijden elkaar in de blauwe curve, die in het vlak $x = y$ ligt. Als je de naar voren wijzende cilinder opensnijdt en de bovenste, grijs gekleurde, helft plat legt, krijg je de gezochte uitslag. Als grootheid op de horizontale as in die uitslag nemen we de rood gemarkeerde booglengte $\ell$, gemeten op de cilinder. Op de verticale as lezen we hoe ver een punt op de cilinder naar voren komt, ofwel, wat de $x$-coördinaat is. En de blauwe curve wordt beschreven door de $x$-coördinaat als functie van de booglengte $\ell$. Om een uitslag te krijgen die zichtbaar aansluit bij de cilindertekening laten we de positieve $x$-as naar beneden wijzen.

Volgens de definitie is de booglengte $\ell$ gelijk aan de bijbehorende hoek in radialen. Als $\vartheta$ de hoek met de positieve $y$-as is, kunnen we de eenheidscirkel gebruiken om de $y$ en $z$-coördinaten te beschrijven: $y = \cos(\vartheta)$ en $z = \sin(\vartheta)$. De hoek behorend bij $\ell$ is in de figuur gelijk aan $\tfrac{\pi}{2}-\vartheta$. Trekken we een lijn evenwijdig aan de $x$-as tot de blauwe snijcurve, dan geldt in ieder van de punten op die lijn dat $y = \cos(\vartheta)$ en $z = \sin(\vartheta)$. Op de snijcurve geldt $x = y$, en dus geldt voor ieder punt op de groene lijn op de tweede cilinder dat $x = \cos(\vartheta)$. En we concluderen dat $x = \cos(\vartheta) = \sin(\tfrac{\pi}{2} -\vartheta) = \sin(\ell)$ voor ieder punt op de blauwe snijcurve.

Gebruikmakend van deze curve kunnen we een uitslag maken voor een van de twee cilinders door in één grafiek te tekenen:

	$y=\sin(x)$,		$-\tfrac{\pi}{2}\le x\le \tfrac{\pi}{2}$,
	$y=-\sin(x)$,		$-\tfrac{\pi}{2}\le x\le \tfrac{\pi}{2}$,
	$x=\tfrac{\pi}{2}$,		$|y| \ge 1$,
	$x=-\tfrac{\pi}{2}$,		$|y| \ge 1$.

Met een identieke uitslag voor de tweede, loodrecht snijdende cilinder kun je dan gebruikmakend van plakranden een kruisgewelf bouwen, zie figuur 8.

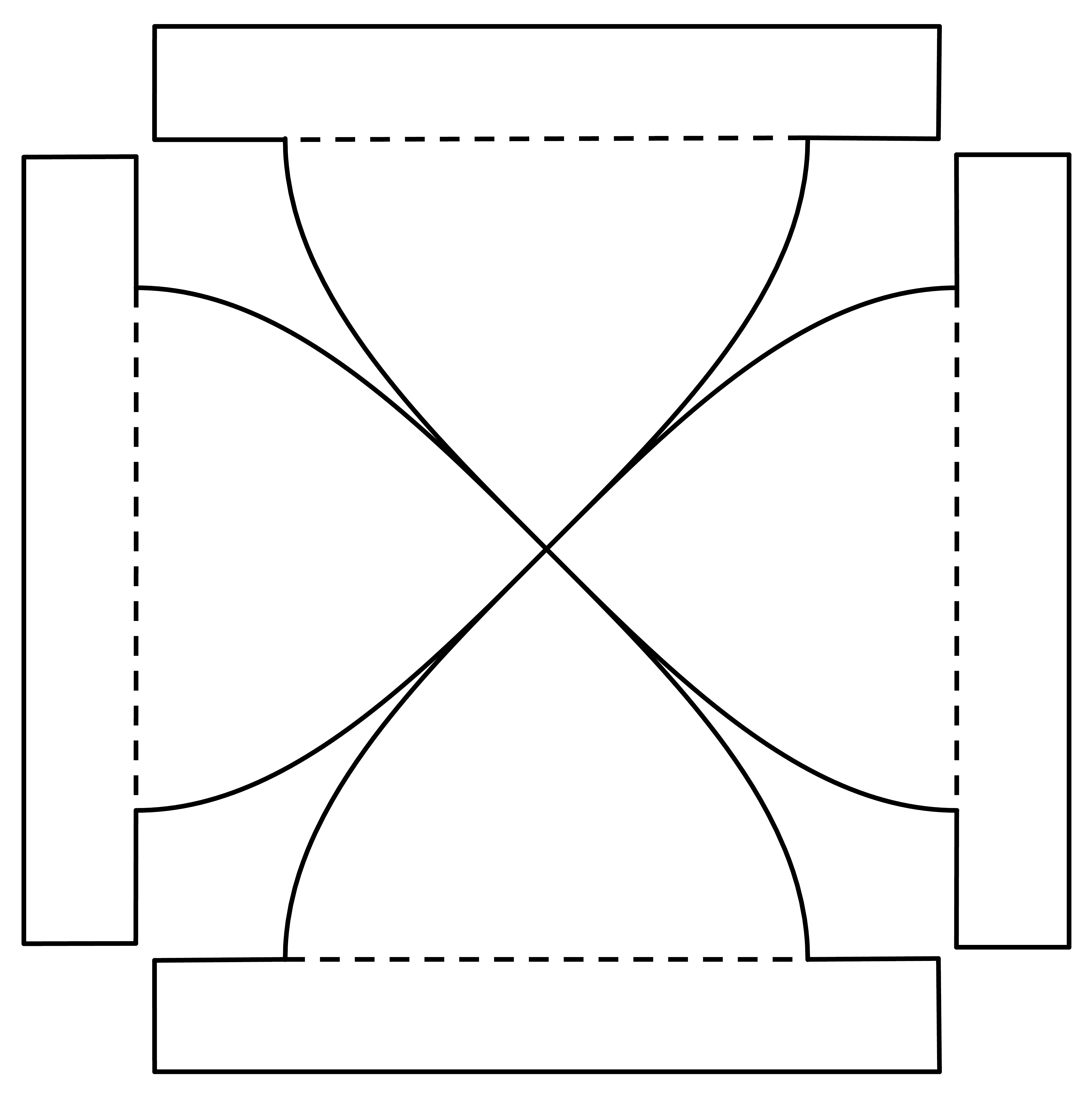Figuur 8: Vouwblad met plakranden voor een deel kruisgewelf en buiten- en binnenaanzicht van het resultaat; vouwblad met plakranden voor kloostergewelf en resultaat.

Dezelfde curve definieert ook een vouwplaat voor een kloostergewelf. Daarvoor gebruiken we precies die delen die bij het kruisgewelf worden weggeknipt. Van deze vier delen kun je in één keer een complete bouwplaat maken door voor de kruisende cilinder de inverse functies van $y = \sin(x)$ en $y = -\sin(x)$ te tekenen:

	$y=\sin(x)$,		$-\tfrac{\pi}{2}\le x\le \tfrac{\pi}{2}$,
	$y=-\sin(x)$,		$-\tfrac{\pi}{2}\le x\le \tfrac{\pi}{2}$,
	$y=\sin^{-1}(x)$,		$-1 \le x \le 1$,
	$x=-\sin^{-1}(x)$,		$-1 \le x \le 1$.

Plakranden toevoegen helpt ook hier om het gewelf in elkaar te zetten en stevigheid te geven. Zie de figuur voor de vouwplaat en het resultaat. Je kunt de vouwplaten ook onder aan deze pagina vinden onder [documenten]. Om de gewelven te bouwen moet je bij het uitknippen telkens net niet doorknippen tot aan het kruis om één stuk papier te houden. We keren terug naar Lipari, naar de kloosterkerk. Die heeft zoals gezegd een puntig in plaats van een cilindervormig gewelf.

Dit gewelf is in de negentiende eeuw gebouwd ter vervanging van een tongewelf, dat na een blikseminslag verloren was gegaan.

De bouw van zo'n gewelf met een puntige basisvorm verloopt net zoals de bouw van een cilindervormig kruisgewelf. Zoals in figuur 6 kun je ook voor een puntig gewelf op de grond uitlijnen hoe de diagonaal eruit zal zien. En ook voor een puntig gewelf, bestaande uit twee cirkelbogen, kun je een uitslag tekenen die kan dienen als mal voor de constructie van een maquette. Als voorbeeld nemen we hier een 'gelijkzijdige' boog, met twee cirkelbogen gebaseerd op een gelijkzijdige driehoek. Beide kruisende gewelven hebben weer dezelfde vorm, zodat op de blauwe snijcurve weer geldt dat $y = x$. Om een uitslag te maken beschrijven we net als in figuur 7 de afstand $x$ als functie van de booglengte $\ell$.

Met de gekozen hoeken $\alpha$ en $\beta$ zoals in het vooraanzicht in figuur 9 vinden we $\cos(\alpha) =  \frac{1+x}{2}$. De boog is gebaseerd op een cirkel met straal $2$ en dus is de booglengte $\ell = 2\beta$ met $\beta = \tfrac{\pi}{3}-\alpha=\tfrac{\pi}{3}-cos^{-1}\left(\frac{1+x}{2}\right)$ voor $x \in [0,1]$, ofwel $x = 2\cos\left(\tfrac{\pi}{3}-\tfrac{\ell}{2}\right) - 1$ voor $\ell \in [0, \tfrac{2\pi}{3}]$. De resulterende curve lijkt op een kwart periode van een horizontaal uitgerekte sinus-grafiek, maar is dat net niet. Zie figuur 9.

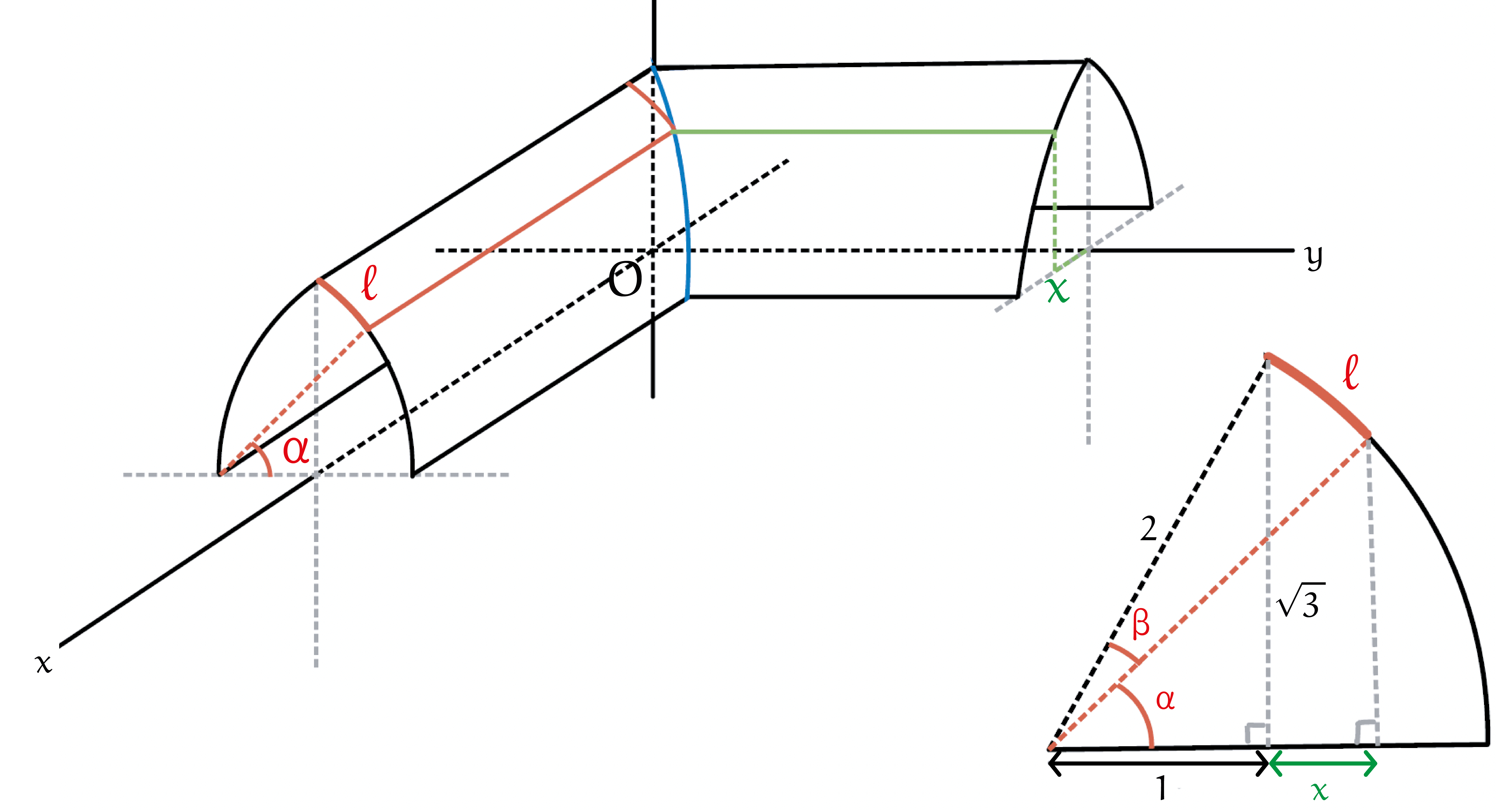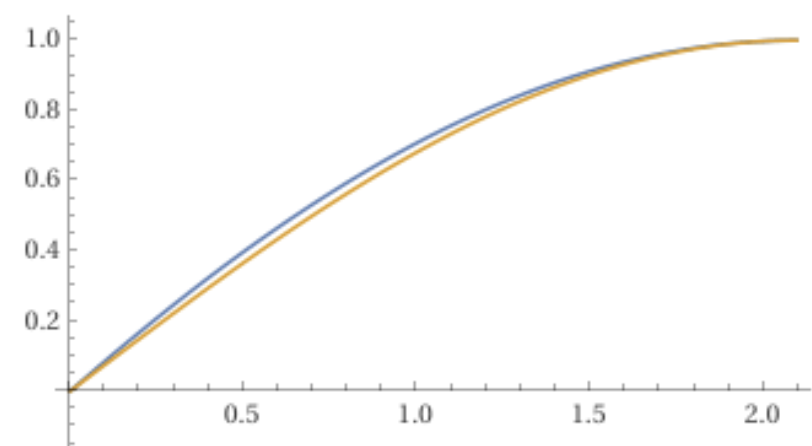Figuur 9: Curve $x(\ell)$ voor de uitslag van een halve puntige boog. $\color{blue}{Blauw}$: de exacte curve $x = 2\cos\left(\tfrac{\pi}{3}-\tfrac{\ell}{2}\right)-1$. $\color{gold}{Geel}$: de uitgerekte sinusgrafiek sinusgrafiek $x = \sin\left(\tfrac{3\ell}{4}\right)$.

Hoewel de bouwplaat voor zo'n puntig gewelf er op het eerste gezicht hetzelfde uitziet als een geschaalde versie van die voor een cilindervormig kruisgewelf, is hij dus net iets anders. In het bijzonder is de richtingscoëfficiënt van de twee delen niet gelijk aan $\pm1$ zoals in figuur 8, maar is hij voor het ene deel gelijk aan $\pm\sin\left(\tfrac{\pi}{3}\right) = \pm\tfrac{\sqrt{3}}{2}$ en voor de kruisende curves aan $\pm\tfrac{2}{\sqrt{3}}$. Als je wilt voorkomen dat bij de bouw "met passen en meten de tijd wordt versleten" moet je blijkbaar iets meer rekenen voor een majestueuzer resultaat.