De regels van Go zijn zo simpel dat er interessante wiskundige structuren in naar voren komen. Go wordt gespeeld op een vierkant bord, met doorgaans 19 × 19 kruispunten in een raster. Maar kleiner is voor beginners misschien wel prettiger. Om beurten plaatsen de twee spelers (zwart en wit) een go-steen op een kruispunt; die steen blijft daar verder staan (tenzij hij geslagen wordt, zie regel 4). De go-stenen zien er uit als Mentos, in diagrammen worden ze getekend als zwarte en witte cirkels. Wie de meeste stenen kan neerzetten wint. (In de praktijk zijn er wat manieren om overeen te komen eerder te stoppen als de eindstand wel duidelijk is en dan de uitkomst te tellen.) Stenen van dezelfde kleur vormen ketens, verbonden via de lijntjes van het raster; zo'n keten vormt één geheel. Een keten zonder vrije naastliggende kruispunten (dat heten vrijheden) mag niet op het bord blijven liggen. Als je een zet doet die de laatste vrijheid van een keten (van de tegenstander) wegneemt, dan moet je die keten van het bord verwijderen. Stenen zonder vrijheden mogen niet op het bord staan (behalve dus heel even tijdens het 'slaan' van stenen van de tegenstander). Een bordpositie mag tijdens een partij niet herhaald worden.

 

1A

1B

1C

1D

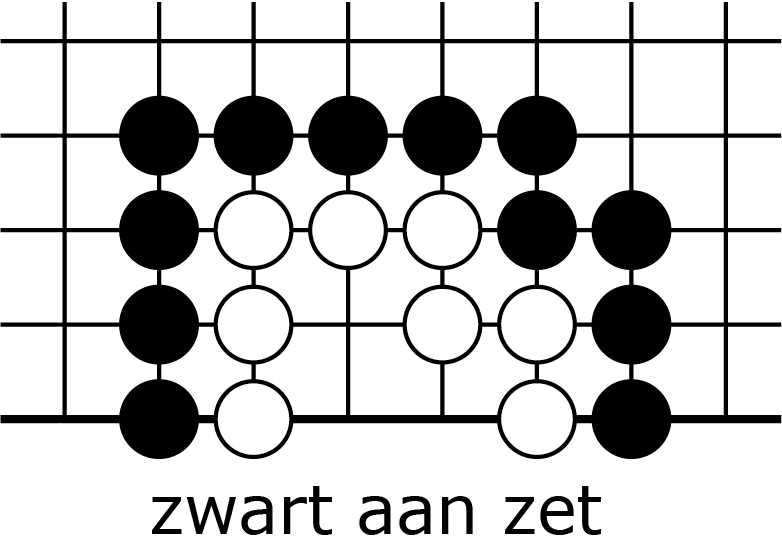
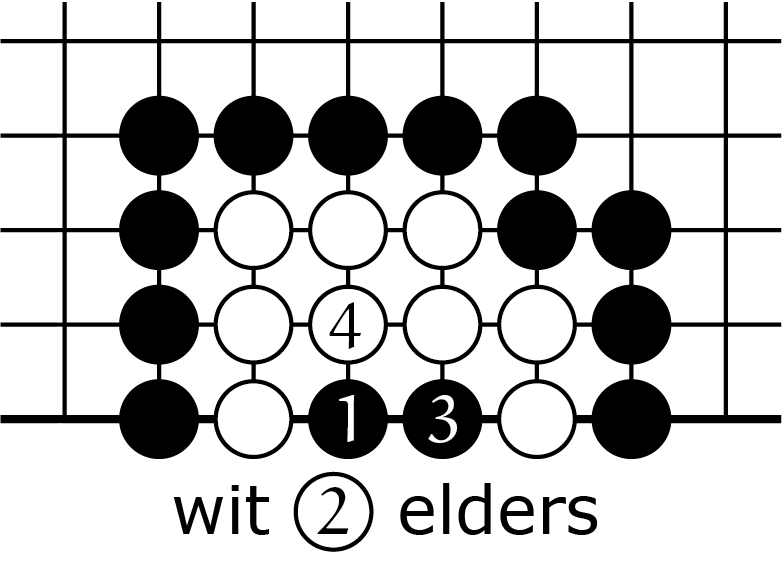
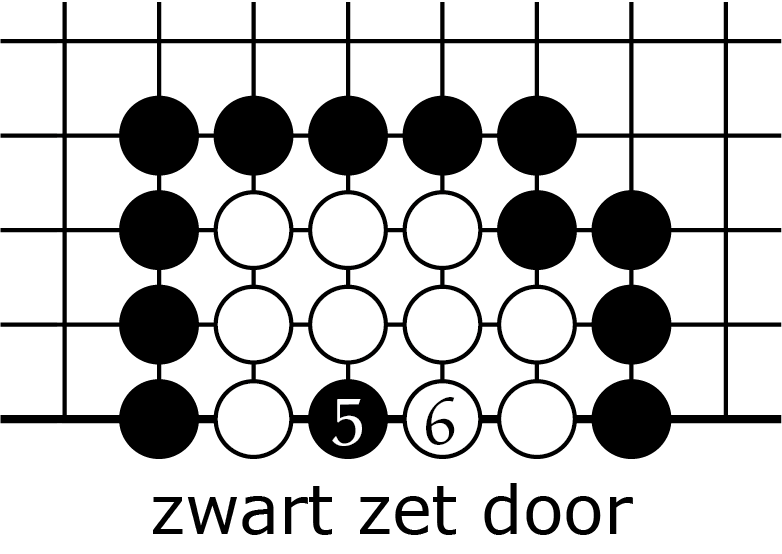
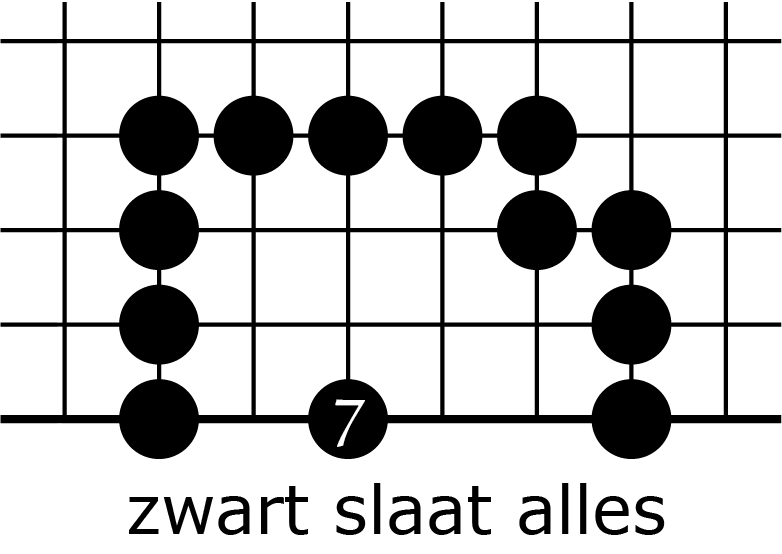
In figuur 1 brengen we het slaan nog een keer in herinnering.

We gaan nu uitrekenen hoeveel zetten er nodig zijn om een keten feitelijk te slaan. Bij een aantal van $n$ vrijheden zijn er steeds $n - 1$ zetten nodig om atari te zetten, waar wit dan meteen op reageert door te slaan; dus heeft wit $n - 2$ zetten elders kunnen doen. Vervolgens ontstaat een keten met $n - 1$ binnenvrijheden. Het proces herhaalt zich dan: dat is nou recursie. Dus als we $Z_n$ definiëren als 'het aantal zetten dat zwart nodig heeft om een keten met n binnenvrijheden te slaan', dan hebben we, voor $n > 2$, de recursieve formule:

$$Z_n=(n-2)+Z_{n-1}.$$

En bovendien weten we dat $Z_3 = 3$, want zo waren we begonnen. (Ja, ook dat $Z_1 = 1$, maar er is zo meteen een verrassing.) Iets met een lineair groeiend verschil (want de verandering $Z_n - Z_{n-1} = n - 2$ hangt gestaag af van $n$) moet zelf kwadratisch zijn. We stellen daarom $Z_n = an^2 + bn + c$, en met wat rekenwerk krijgen we:

$$Z_n-Z_{n-1}=((an^2+bn+c))-(a(n-1)^2+b(n-1)+c)=2an-a+b.$$

Dat moet gelijk zijn aan $n - 2$, dus $a = \tfrac{1}{2}$ en $b = -\tfrac{3}{2}$. Als we dan invullen dat $Z_3$ gelijk aan $3$ moet zijn, dan leren we wat $c$ is. We vinden uiteindelijk:

$$Z_n=\tfrac{1}{2}n^2-\tfrac{3}{2}n+3.$$

In de tabel staat wat de formule geeft voor een opeenvolging van waarden van $n$:

$n$	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$\ldots$
$Z_n$	$2?$	$2$	$3$	$5$	$8$	$12$	$17?$	$\ldots$

Voor $Z_3$ en $Z_4$ klopt de formule alvast met wat we boven deden, en we leren nu ook dat $Z_5 = 8$ zonder stellingen te hoeven uitspelen. Maar volgens de formule zou je $Z_1 = 2$ zetten nodig hebben om een keten met $1$ vrijheid te slaan – en dat is niet waar?! De reden is dat het echte patroon van atari zetten en terugslaan (waarop we de formule baseerden) zich daar nog niet heeft gevormd, dat is pas vanaf $n = 2$ (zie bijvoorbeeld figuren 4C-E uit het vorige artikel). Dat $Z_0 = 3$ is natuurlijk helemaal onzin. De formule heeft dus een beperkte geldigheid, dat is wel vaker zo met dit soort tel-formules.

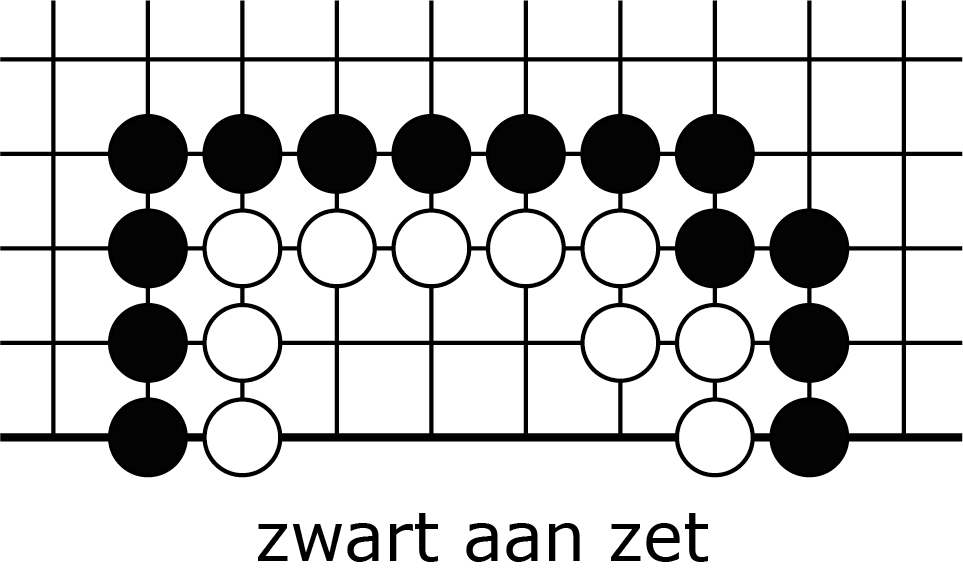
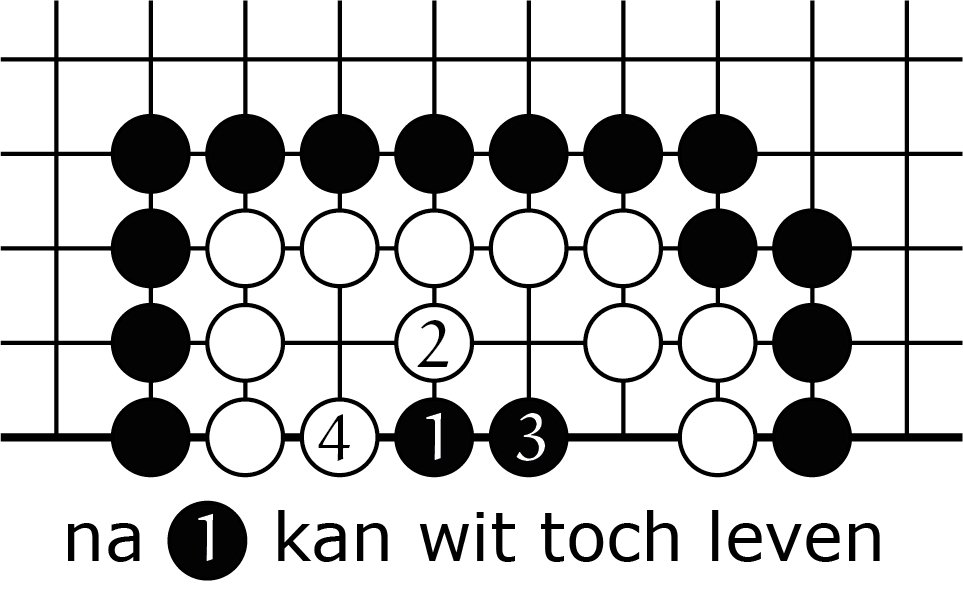
En volgens de tabel zou je $Z_7 = 17$ zetten nodig hebben om een keten met $7$ vrijheden te slaan; maar als je meer go speelt, merk je wel dat zo'n keten 'te groot' is om te slaan. Meestal leeft de keten gewoon omdat je twee ogen kunt maken (zoals in figuur 2A en B): zwart kan wit niet meer slaan.

2A

2B

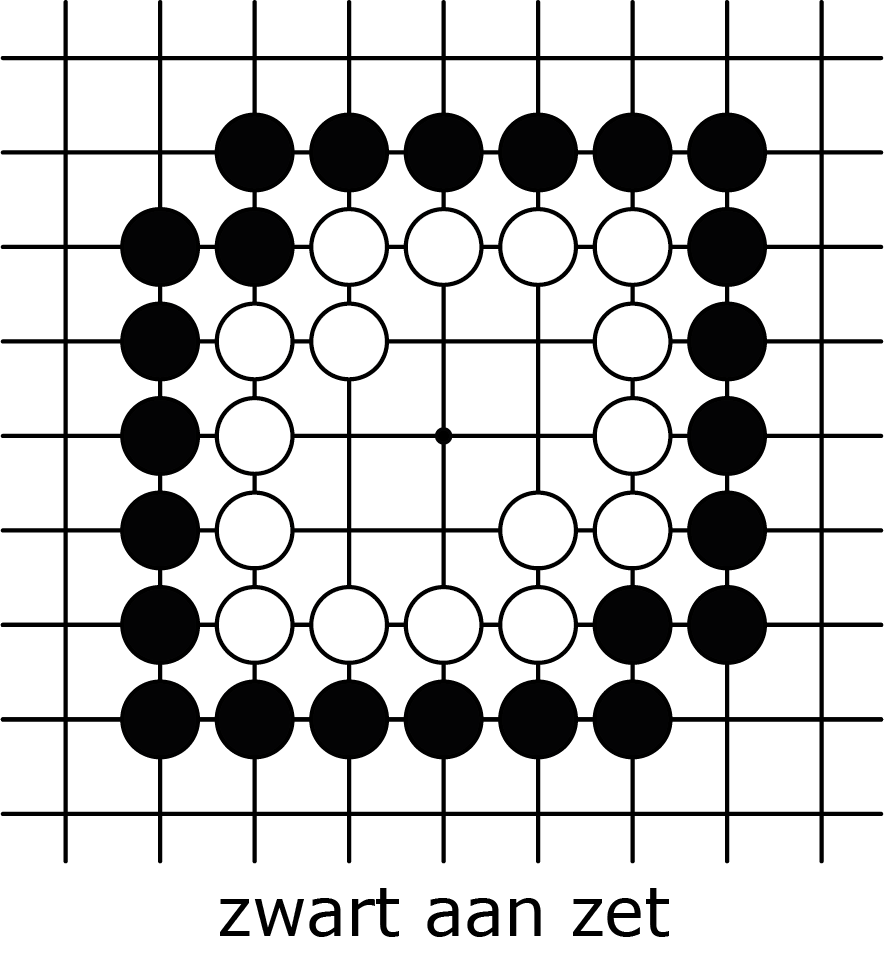
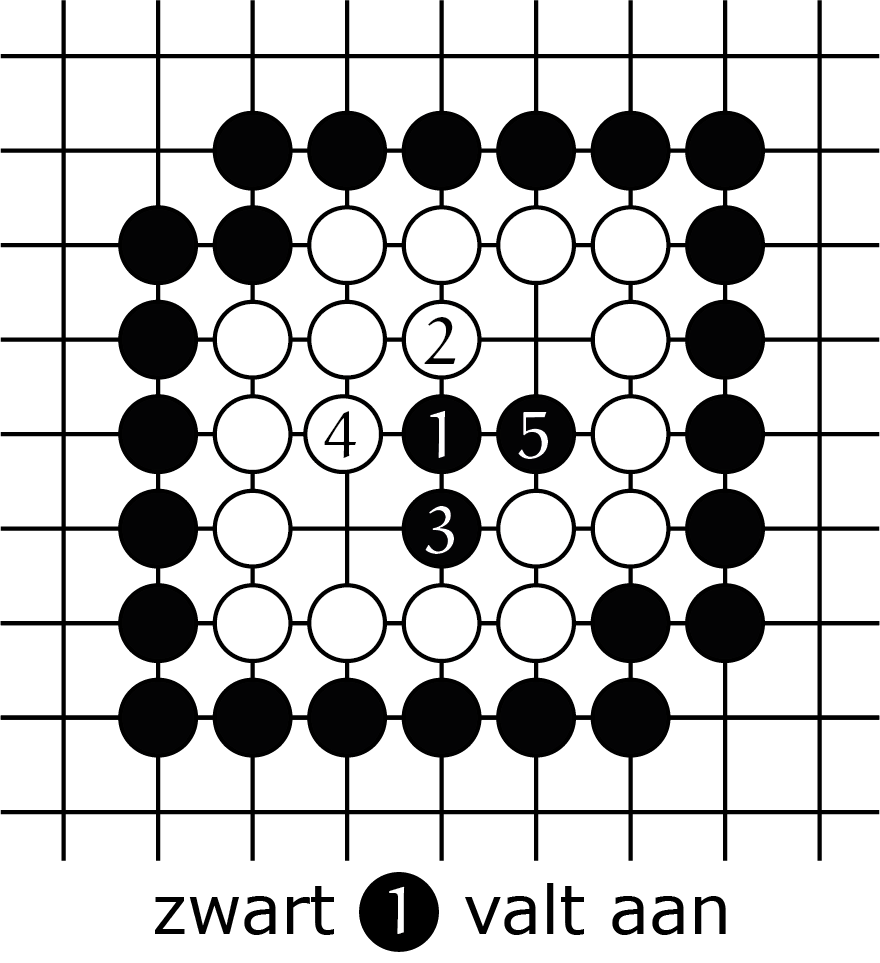
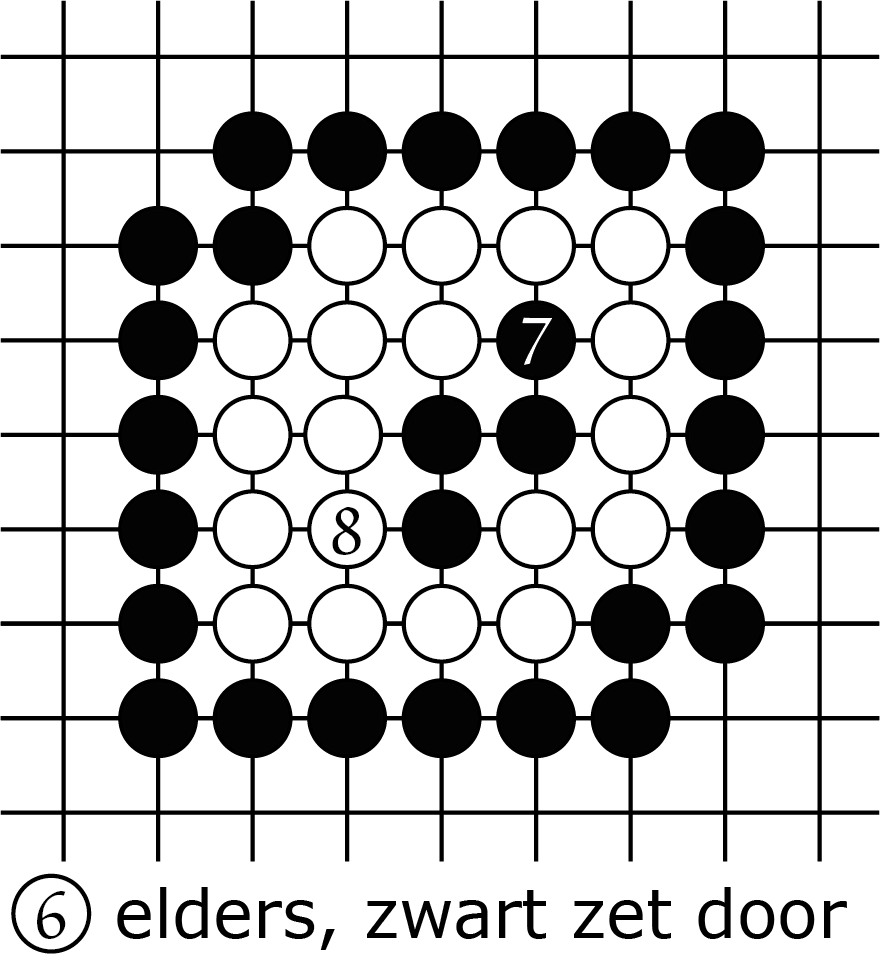
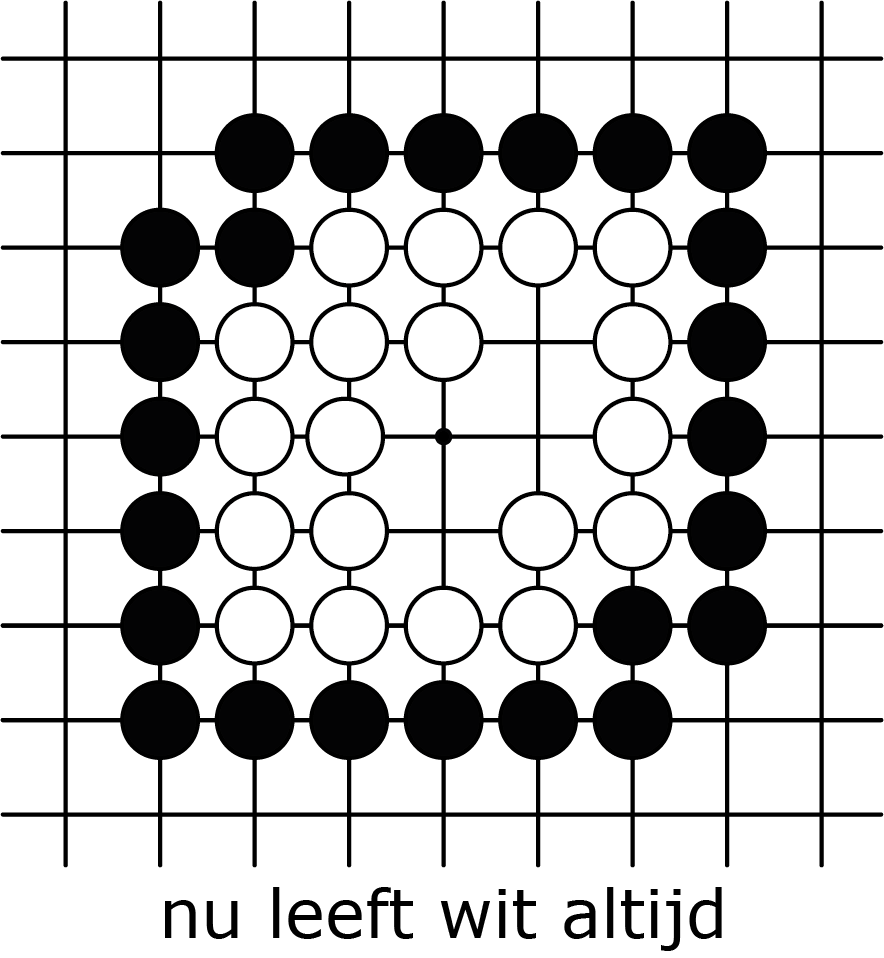
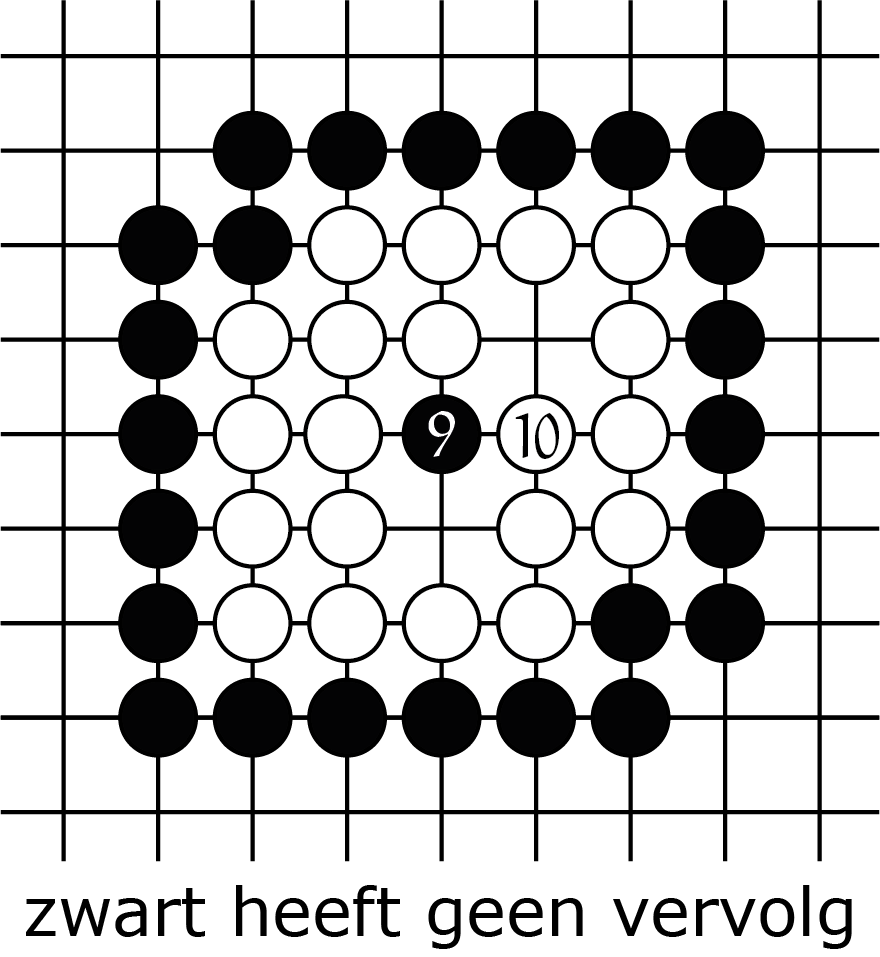
Toch kan er ook nog net een seki ontstaan, dat is een stelling waarbij geen van beide spelers de andere kan slaan. Het is een stelling die niet levend is, maar ook niet dood! Dat gebeurt met de witte keten in figuur 3A, die een nogal rond pleintje van $7$ binnenvrijheden heeft. Als wit speelt op dat punt in het midden, dan heeft hij twee ogen en leeft dus. Maar dat hoeft eigenlijk niet, want zwart kan de witte stelling toch niet doden. We zien in 3C hoe wit de sterkst mogelijke zwarte aanval pareert. De situatie na 3C is stabiel en heeft geen vervolgzet nodig.

3A	3B	3C
3D	3E	3F

Zwart kan niet zetten zonder geslagen te worden in 3D; dan ontstaat 3E, een groep met $4$ binnenvrijheden op een rij, en die kan altijd leven zoals 3F laat zien. Dus kan zwart beter niet aanvallen. En we vinden dus dat de formule nog subtieler is, want $Z_4 = 5$ geldt niet voor de keten in 4E! Alleen binnenvrijheden tellen is niet voldoende, de vorm van de keten doet er ook toe!

Maar aan de andere kant, wit kan in 3C de zwarte stenen niet gaan slaan zonder zichzelf atari te zetten, dus zet ook liever ergens anders. De stelling van 3C is daarmee een soort locale patstelling, en die zal zo op het bord blijven staan tot het einde van de partij, en dan tel je de stenen die mogen blijven staan (in onze simpele wiskundige variant van de regels, in Japan telt men dit anders). Net als bij 'twee ogen leeft' zien we dat de eenvoudige regels van go tot wat verrassingen leiden voor ketens.

Het blijkt dus dat de formule voor $Z_n$ spaak loopt bij $n = 7$: er is geen vorm van $7$ binnenvrijheden die echt in $17$ zetten geslagen kan worden, bij de juiste verdediging. (Tenzij je twee zetten achter elkaar kunt doen, en dat kan voorkomen als er een 'ko' op het bord komt – maar dat is een ander verhaal…).

Deze simpele en nette situaties zijn nog wel uit te rekenen. Maar feitelijk omsingelen van de minder strak geformeerde groepjes stenen die in natuurlijke partijen voorkomen is niet makkelijk. Het totale go-spelen vergt heel wat meer, en de 'vage' fase van het spel met het plannen waar je jouw groepjes begint om uiteindelijk zoveel mogelijk stenen te mogen plaatsen is knap lastig. En dus leuk en uitdagend, als je zo in elkaar zit…

		Er zijn veel bronnen op het internet om een gevoel te krijgen voor de rijkdom van go, van beginnerscursussen tot becommentarieerde profpartijen, bijvoorbeeld op senseis.xmp.net. De Nederlandstalige website 312go.org/home heeft een gratis online cursus, omsingelpuzzeltjes (dat heet 'tsumego') en voorbeeldpartijen. Speel er eens mee!

 

Puzzeltje

$\color{teal}{Zin\ om\ eens\ langs\ te\ komen\ op\ een\ go-club?}$
$\color{teal}{Zie }$ www.goband.nl $\color{teal}{voor\ clubs\ bij\ jou\ in\ de\ buurt.}$