
Go spelen: op je tellen passen
[oOO]
Go is een van origine Oosters bordspel. Het is al heel oud, en toch is iedere partij die je speelt nieuw en opwindend. Go is minstens zo gecompliceerd als schaken – sinds kort (medio 2016) kunnen alleen computerprogramma’s zoals AlphaGo ons mensen vertellen hoe het eigenlijk gespeeld zou moeten worden. Maar ook zonder zelf een computer te zijn kan je er veel plezier aan beleven.
|
De regels van Go zijn zo simpel dat er interessante wiskundige structuren in naar voren komen.
|
||||
Hoewel je dus individuele stenen plaatst, zijn de ontstane ketens en hun vrijheden eigenlijk de basiseenheden van het spel. Laten we een voorbeeld doen, op een klein stukje bord (voor een kleine partij, zie rrehm.home.xs4all.nl/dropjes.pdf).
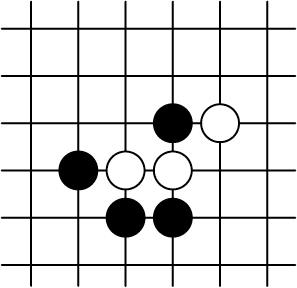
1A |
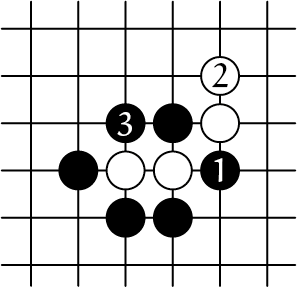
1B |
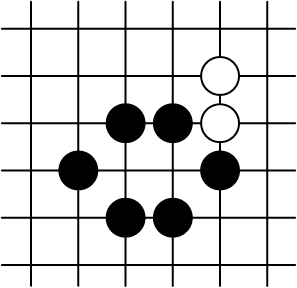
1C |
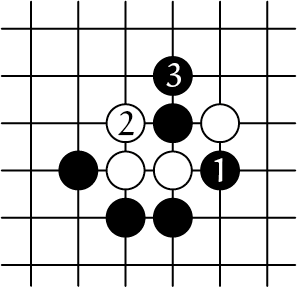
1D |
De witte keten van twee stenen in 1A heeft nog twee vrijheden. Zwart en wit spelen nu wat zetten ![]() ,
, ![]() ,
, ![]() in 1B. Oeps! De witte keten van twee stenen wordt geslagen door zwart, door
in 1B. Oeps! De witte keten van twee stenen wordt geslagen door zwart, door ![]() . Daardoor ontstaat de positie in 1C. Wit heeft nu minder stenen op het bord, dus dat kost punten!
. Daardoor ontstaat de positie in 1C. Wit heeft nu minder stenen op het bord, dus dat kost punten!
Wit had er wel iets tegen kunnen doen, zet ![]() in 1B was niet zo handig. Liever
in 1B was niet zo handig. Liever ![]() in 1D, daarmee krijgt wit twee vrijheden en dreigt zelfs een zwarte steen te slaan (door op het punt van
in 1D, daarmee krijgt wit twee vrijheden en dreigt zelfs een zwarte steen te slaan (door op het punt van ![]() te spelen). Zwart heeft dat verdedigd door met 3 die steen te verlengen tot een keten van twee stenen (met drie vrijheden).
te spelen). Zwart heeft dat verdedigd door met 3 die steen te verlengen tot een keten van twee stenen (met drie vrijheden).
2A |
2B |
2C |
2D |
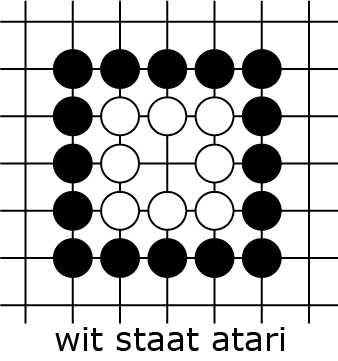
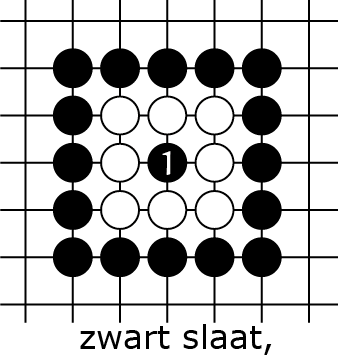
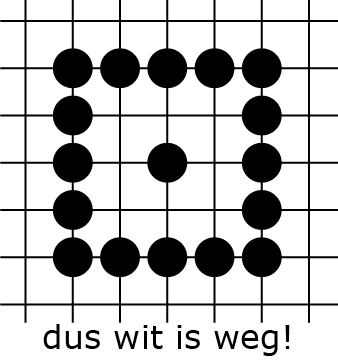
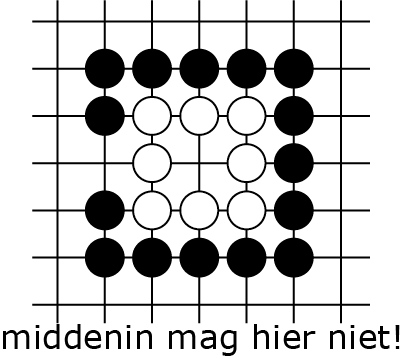
Voor de duidelijkheid: een keten met maar één vrijheid (we zeggen dat die 'atari staat') kan bij de volgende zet geslagen worden (als regel 5 dat toestaat), zelfs als je daarvoor zelf even een keten zonder vrijheden op het bord krijgt tijdens het zetten. Dus in stelling 2A mag zwart op het middenpunt spelen 2B en slaat dan de witte groep 2C. Maar in 2D mag dat niet, zwart moet eerst de zet van buitenaf spelen zodat wit echt nog maar één vrijheid heeft. Dat is genoeg over de regels, we gaan nu vechten! Een lokaal gevecht ontstaat als twee groepen elkaar aan het omsingelen zijn. Wie is er eerder bij en kan de andere slaan? Dat blijkt nog behoorlijk subtiel te kunnen worden: een keten kan veel meer vrijheden hebben dan op het eerste gezicht lijkt. Zelfs 'kwadratisch veel meer'! In het vervolgartikel gaan we daar een formule voor afleiden. Nu gaan we eerst begrijpen wat er speelt.
Bij het oplossen van dit soort wiskundige tel-problemen is het gebruikelijk om 'recursie' te gebruiken. Je beziet of je een ingewikkelder situatie kan reduceren tot iets eenvoudigers, en die tot nog eenvoudiger, totdat je hem kunt oplossen. En je houdt bij hoeveel zetten je steeds moet doen voor die reductie; aan het eind tel je alles op.
3A |
3B |
3C |
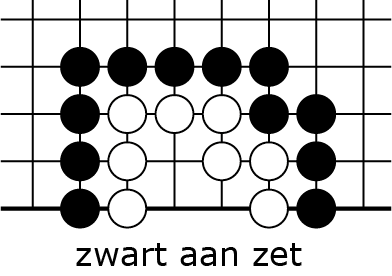
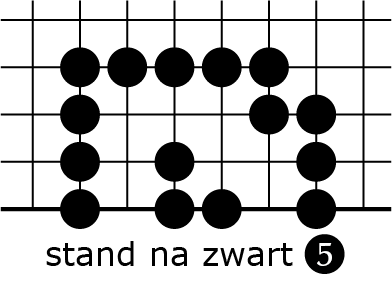
Bijvoorbeeld, als zwart een witte keten met drie interne vrijheden helemaal heeft omsingeld, heeft hij dan ook drie zetten nodig om hem van het bord te halen? In ieder geval op zijn minst drie, zoals de diagrammen 3A-C laten zien: (Om ruimte te besparen bestuderen we dit voor een stelling aan de bordrand, aangegeven door een dikke lijn. Het aantal vrijheden voor een punt aan de rand is $3$, want er zijn drie bordpunten via de lijntjes verbonden. Je kunt de principes die we hier ontdekken echter makkelijk overdragen naar een stelling midden op het bord.)
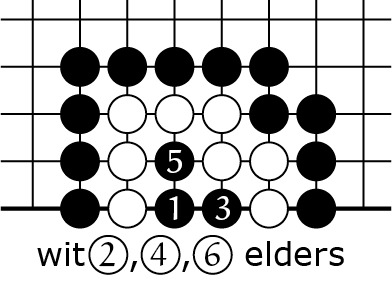
Terwijl zwart drie zetten doet om te slaan in figuur 3B, heeft wit intussen op drie plaatsen elders op het bord kunnen spelen met ![]() ,
, ![]() ,
, ![]() (totdat zwart weer aan zet is) en misschien waren dat wel heel nuttige zetten voor haar. Het nemen van de witte keten houdt zwart dus in feite drie zetten bezig.
(totdat zwart weer aan zet is) en misschien waren dat wel heel nuttige zetten voor haar. Het nemen van de witte keten houdt zwart dus in feite drie zetten bezig.
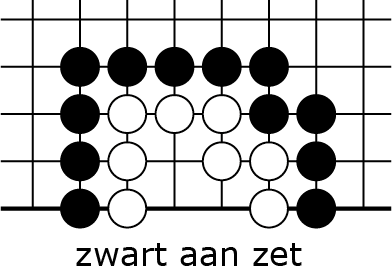
Maar misschien had wit zich nog beter kunnen verweren, bijvoorbeeld na zwart ![]() ?
?
4A |
4B |
4C |
|
4D |
4E |
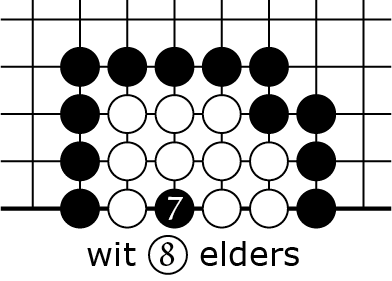
4F |
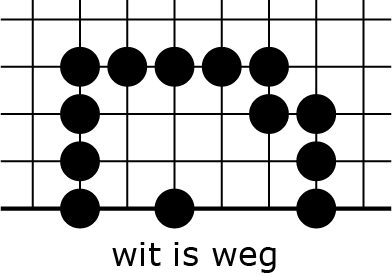
4G |
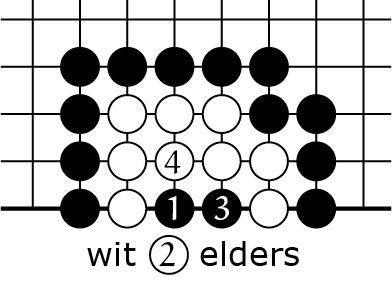
Je begint met zwart ![]() in 4B; als wit nu een eigen vrijheid bezet met
in 4B; als wit nu een eigen vrijheid bezet met ![]() dan kan je de keten pakken met
dan kan je de keten pakken met ![]() ; dus wit kan zet
; dus wit kan zet ![]() beter ergens anders op het bord spelen. Dan zet je zwart
beter ergens anders op het bord spelen. Dan zet je zwart ![]() , en nu zou je met de volgende zet de witte keten kunnen slaan, want zij heeft nog maar één vrijheid. Wit voorkomt dat door jou te slaan met
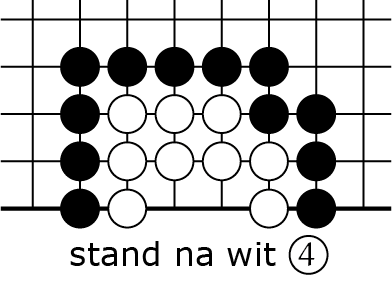
, en nu zou je met de volgende zet de witte keten kunnen slaan, want zij heeft nog maar één vrijheid. Wit voorkomt dat door jou te slaan met ![]() in 4B, zo onstaat 4C. Daarna kom je terug met
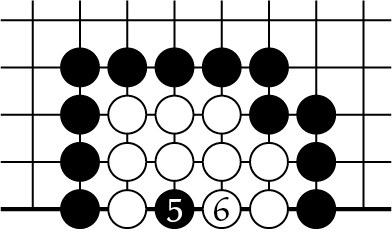
in 4B, zo onstaat 4C. Daarna kom je terug met ![]() in 4D, weer staat wit atari. In de volgende zet kan zwart wit pakken; zelf als wit nog even met
in 4D, weer staat wit atari. In de volgende zet kan zwart wit pakken; zelf als wit nog even met ![]() slaat in 4D, dan nog is zwart
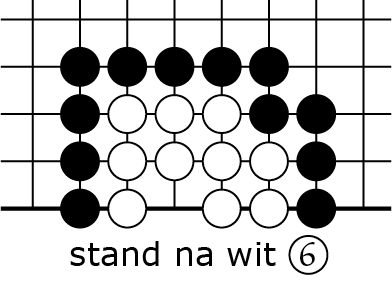
slaat in 4D, dan nog is zwart ![]() in 4F de doodsklap. Maar je ziet dat wit nu maar twee keer elders op het bord heeft kunnen spelen, met
in 4F de doodsklap. Maar je ziet dat wit nu maar twee keer elders op het bord heeft kunnen spelen, met ![]() en
en ![]() , dus dit is een minder goede mogelijkheid voor wit dan wat er in 3A-C gebeurde.
, dus dit is een minder goede mogelijkheid voor wit dan wat er in 3A-C gebeurde.
Overigens: je kunt het als zwart ook goed fout doen! Dat zie je in 5A-C:
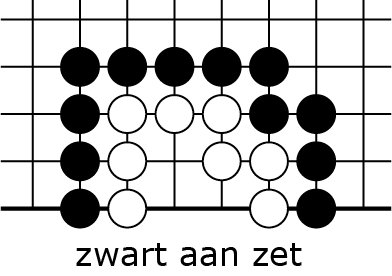
5A |
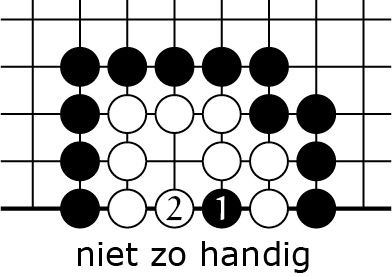
5B |
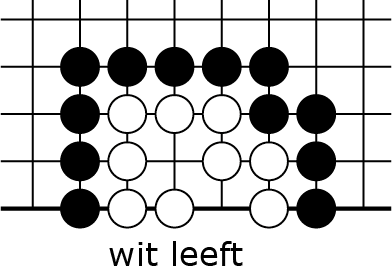
5C |
Als zwart begint ![]() in 5B, dan slaat wit
in 5B, dan slaat wit ![]() de zwarte steen. Nu ontstaat een stelling in 5C waarin zwart niet op de twee laatste vrijheden kan (of mag) spelen: hij zou dan een steen op het bord zetten die geen vrijheden heeft, en zonder dat hij daarmee de laatste vrijheid van een witte keten wegneemt. De witte keten die is ontstaan in 5C kan niet geslagen worden: we zeggen dat een keten met twee ogen 'leeft'. Dat soort levende ketens worden eigenlijk de eenheden waarin je denkt als je go speelt; het zijn als het ware je (schaak) stukken, maar je maakt ze zelf en ze zijn iedere keer weer anders. Het is esthetisch wel bevredigend om te zien dat deze grotere denkeenheden vanzelf ontstaan uit de spelregels op het niveau van ketensen vrijheden...
de zwarte steen. Nu ontstaat een stelling in 5C waarin zwart niet op de twee laatste vrijheden kan (of mag) spelen: hij zou dan een steen op het bord zetten die geen vrijheden heeft, en zonder dat hij daarmee de laatste vrijheid van een witte keten wegneemt. De witte keten die is ontstaan in 5C kan niet geslagen worden: we zeggen dat een keten met twee ogen 'leeft'. Dat soort levende ketens worden eigenlijk de eenheden waarin je denkt als je go speelt; het zijn als het ware je (schaak) stukken, maar je maakt ze zelf en ze zijn iedere keer weer anders. Het is esthetisch wel bevredigend om te zien dat deze grotere denkeenheden vanzelf ontstaan uit de spelregels op het niveau van ketensen vrijheden...
Bij drie binnenvrijheden zijn er dus drie zetten nodig, dat lijkt logisch, want terloops zagen we in 4C-G dat bij twee vrijheden twee zetten nodig zijn, en in 4E-G dan één vrijheid ook één zet kost. Voor vier binnenvrijheden dus vier zetten? Laten we eens kijken naar 6A, zo'n keten met vier binnenvrijheden.
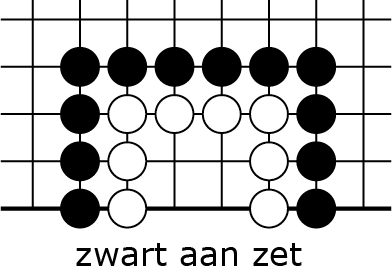
6A |
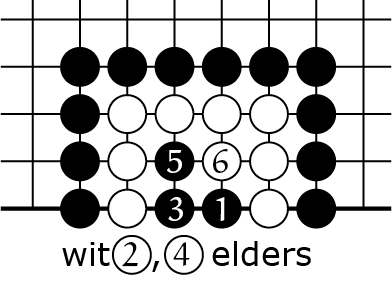
6B |
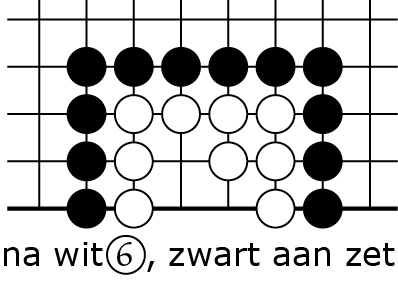
6C |
We beginnen met volzetten met zetten ![]() ,
, ![]() ,
, ![]() (terwijl wit dus twee zetten ergens anders speelt). Nu staat wit atari dus moet reageren met
(terwijl wit dus twee zetten ergens anders speelt). Nu staat wit atari dus moet reageren met ![]() . Daardoor slaat wit zwart, en ontstaat 6C. Hee, dit herkennen we, dat is precies wat we eerder hebben gezien: drie binnenvrijheden, dus drie zetten. In totaal heeft wit vijf zetten ergens anders kunnen spelen voordat hij werd geslagen, dus om vier binnenvrijheden op te vullen heb je vijf zetten nodig.
. Daardoor slaat wit zwart, en ontstaat 6C. Hee, dit herkennen we, dat is precies wat we eerder hebben gezien: drie binnenvrijheden, dus drie zetten. In totaal heeft wit vijf zetten ergens anders kunnen spelen voordat hij werd geslagen, dus om vier binnenvrijheden op te vullen heb je vijf zetten nodig.
Hoe gaat dit verder? Je kunt het spelenderwijs ontdekken, maar je kunt ook wiskundig gaan denken. En dat gaan we doen we in het volgende nummer van Pythagoras!
