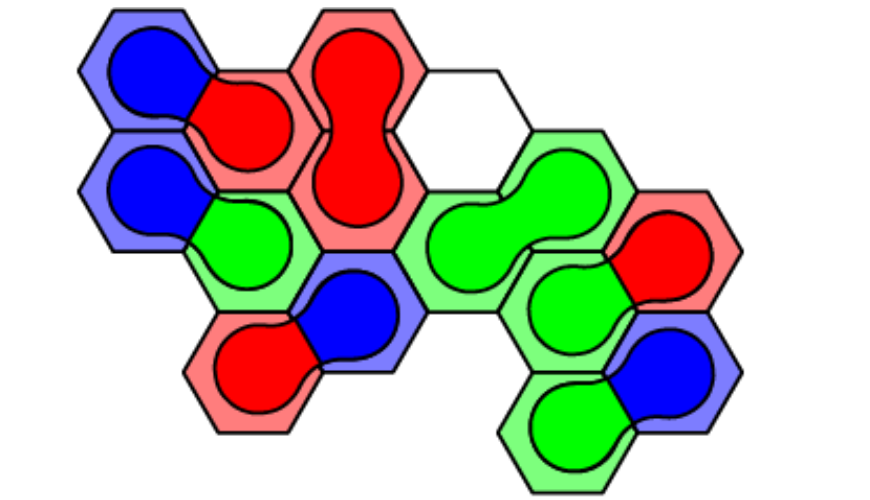
Gourds: een schuifpuzzel met een draai
Schuifpuzzels zijn er in allerlei vormen en maten, iedereen heeft er wel eens één gemaakt. Wat ze gemeen hebben, is dat je moet schuiven: naar links, naar rechts, naar boven of naar beneden. Wat nu als je ook schuin mag of moet draaien?

Eén van de oudere bekende puzzels is de zogenaamde 15-puzzel. Die bestaat uit een vierkant bord met daarin 15 vierkante tegels, genummerd van $1$ tot en met $15$. Deze tegels liggen op de posities van een $4\times 4$ raster, en dus is $1$ plek leeg. Door de tegels te schuiven verandert de plek die leeg is, en kunnen de tegels worden gesorteerd (figuur 1).

Een andere bekende puzzel is Rush Hour. Ook dit is een schuifpuzzel op een raster van vierkanten. Nu zijn de beweegbare stukken iets groter: ze zijn $2$ of $3$ vierkanten groot. Volgens de regels van de puzzel mogen deze "auto’s" niet zijwaarts schuiven, alleen in hun lengterichting. Ze blijven dus altijd in dezelfde rij of kolom. Het doel is altijd om de rode auto naar rechts van het bord af te schuiven (figuur 2).
Als puzzelontwerper probeer je vaak ideeën te combineren, of varianten op ideeën te bedenken die mooi, leuk, elegant en praktisch uitvoerbaar zijn. Enkele jaren geleden was ik op een congres in Japan waar een bekende puzzelwetenschapper, Ryuhei Uehara, een presentatie hield. Na de presentatie sprak ik met een vriend en collega genaamd Yushi Uno: zou het niet mogelijk zijn om een soort Rush Hour te ontwerpen waarin de auto’s de bocht om kunnen? We begonnen onze gedachten met de simpelste versie van zo’n puzzel: alle stukken zijn $2\times 1$, er is maar $1$ cel leeg, en het bord is rechthoekig (figuur 3).

Merk op dat zo’n bord dus altijd een oneven lengte en breedte heeft. Zie je waarom?
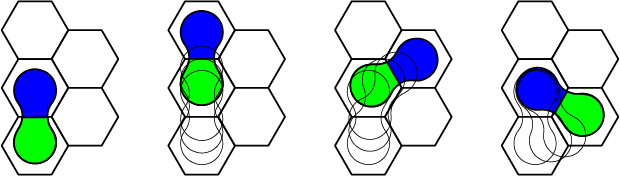
We wilden de stukken kleuren geven, en de opdracht is om de gekleurde stukken op een bepaalde plek te krijgen. In de figuur zie je hoe stukken kunnen verplaatsen op een $3\times 3$ bord. Het groene stukje beweegt de bocht om, hetgeen mogelijk is als de lege cel naast het groene stukje ligt. Daarna beweegt het blauwe stukje rechtdoor, hetgeen mogelijk is als de lege cel in het verlengde ligt van dat stukje. De gekozen vorm van een stukje lijkt enigszins op een flespompoen, ofwel bottle gourd in het Engels. We kozen voor een vorm bestaande uit twee cirkels verbonden door twee cirkelbogen.
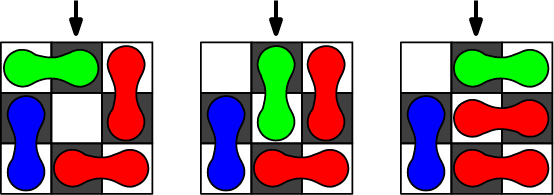
Als je een tijdje met een prototype van zo’n puzzel speelt, dan merk je dat het niet lukt om het groene stukje op de onderste rij te krijgen (figuur 4). Zijn we niet slim genoeg, is het bord misschien te klein, of is er iets structureels aan de hand? Dat laatste. Stel je voor dat het bord is gekleurd zoals een schaakbord. Deze kleuring heeft niets te maken met de rood-groen-blauwe kleuring voor de bestemming van stukjes, zoals voor de puzzel nodig is. De zwart-wit kleuring is alleen bedoeld om een bewijsargument te maken, en is dus denkbeeldig. Omdat het bord een oneven aantal cellen heeft, is er van één kleur cel eentje meer, laten we zeggen van wit.
Elk stukje ligt altijd op een witte en een zwarte cel, en er is altijd een witte cel leeg. Dus: hoe we een stukje ook verplaatsen, het gaat altijd van een zwarte en witte cel naar opnieuw een zwarte en witte cel, en weer zal er een lege witte cel zijn. Nooit zal een zwarte cel leeg worden, want dan passen de stukjes niet meer op de overige cellen.
Maar dat betekent dat een stukje nooit z'n zwarte cel kan 'loslaten'! Elk stukje zal altijd dezelfde zwarte cel bedekken. In de figuur zien we dat het groene stukje altijd de zwarte cel bovenaan, waar de pijl naar wijst, zal bedekken, en dus op één van de drie getoonde plekken zal liggen.
En dus kan het groene stukje niet naar de onderkant verplaatsen. Dit argument is geldig voor elk bord met een oneven aantal cellen waarvan er precies één leeg is. De stukjes kunnen nauwelijks verhuizen over het bord.
Yushi en ik besloten toen om dit soort puzzels te onderzoeken op een hexagonaal raster. Daar lijkt het eerdere probleem niet op te treden: we kunnen immers een bord met een hexagonaal raster niet kleuren met twee kleuren zodat elk stukje altijd op twee verschillende kleuren ligt. Zo'n kleuring bestaat niet.
Laten we eens kijken wat voor bewegingen mogelijk zijn op een hexagonaal raster. Dat blijken er drie te zijn. Als we stukjes als auto zien, dan bestaat rechtdoor, een flauwe bocht en een scherpe bocht. Bij een flauwe bocht verandert de richting met $60^{\rm o}$ en bij een scherpe bocht met $120^{\rm o}$. Daarmee is de scherpe bocht eigenlijk niet uit te voeren, met de vingers. Als we niet de metafoor van een auto gebruiken, dan is het laatste resultaat ook te bereiken door een andere beweging: een draai over $60^{\rm o}$ die we kantelen zullen noemen. Die kantelbeweging is makkelijker uit te voeren met de vingers en heeft minder plaats nodig dan de scherpe bocht. In figuur 5 zie je de drie mogelijke bewegingen.
Vanaf nu nemen we aan dat de puzzel drie soorten verplaatsingen toestaat: gewoon verplaatsen ("vooruit"), een flauwe bocht nemen en kantelen. We kunnen uitrekenen met wat wiskunde hoe groot de stukjes kunnen zijn zodat bij de verplaatsing van een stukje, geen ander stukje opzij geduwd moet worden. Maar we gaan daar in dit artikel niet verder op in.
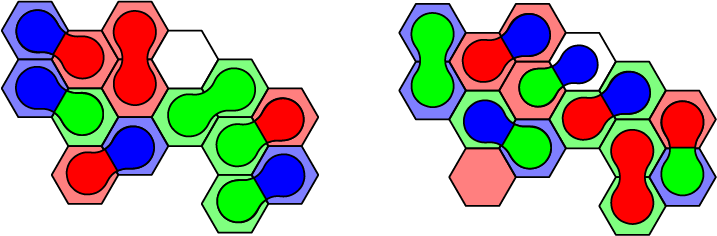
In ons onderzoek hadden we een andere vraag die we wilden beantwoorden: voor welke borden kan je altijd alle stukjes overal krijgen, met behulp van de drie soorten verplaatsingen? We noemen zulke borden herschikbaar. We bestuderen alleen borden met oneven veel hexagonen en zonder afgesloten buitengebied, de normale borden. Een voorbeeld van zo'n puzzel zien we in figuur 6, met links de oplossing en rechts een mogelijke beginsituatie.
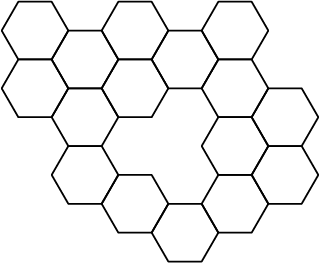
De vraag is dus of we de oplossing altijd kunnen bereiken, onafhankelijk van waar de stukjes beginnen. In figuur 7 met witte hexagonen zien we een bord dat wel een afgesloten buitengebied heeft: het gebied dat drie hexagonen groot is en midden in het eigenlijke bord ligt. Over dit soort borden doen we dus geen uitspraken. We vermoedden dat sommige normale borden wel herschikbaar zijn, en andere niet.
We kwamen er al snel achter dat er een soort normaal bord is dat nooit herschikbaar is: borden die in twee delen uit elkaar vallen als we een hexagon zouden wegnemen, zoals de hexagon waar de blauwe pijl naar wijst links in figuur 8. Deze borden hebben een zogenaamde flessenhals. We krijgen stukjes aan de ene kant van het bord nooit door de flessenhals naar de andere kant. Probeer het maar met halve lucifers of andere langwerpige dingen van de juiste grootte.
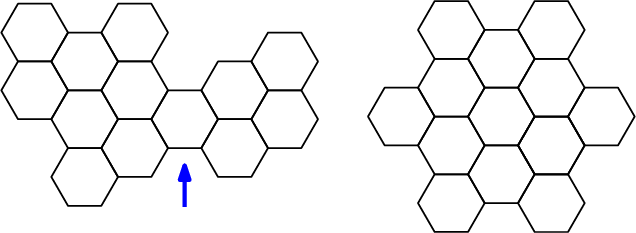
We kwamen er ook achter dat alle andere borden wel herschikbaar zijn, met precies één uitzondering. Deze uitzondering is een bord met 13 cellen dat lijkt op een regelmatige zespuntige ster. Of misschien een sneeuwvlok. Dit bord is rechts in figuur 8 te zien. Dit alles ontdekten we niet alleen, we konden het ook wiskundig bewijzen. Dus alle normale borden zonder flessenhals, en niet de sneeuwvlok, zijn altijd herschikbaar. Dat betekent dat je de stukjes willekeurig op het bord mag gooien, en je kan de puzzel altijd oplossen vanuit deze beginsituatie.
We hebben nog wat meer bewezen dat ook zeer van belang is voor een puzzelontwerper: het aantal verplaatsingen dat nodig is om een puzzel op te lossen is hoogstens kwadratisch in het aantal stukjes. Kortom, er bestaat een kwadratische functie $f(n)$, waarbij $n$ het aantal stukjes van de puzzel is, zodanig dat nooit meer dan $f(n)$ verplaatsingen nodig zijn om de puzzel op te lossen. Dit geldt voor elk bord en elke beginpositie van de stukjes. We noemen de functie $f(n)$ een bovengrens op het aantal benodigde verplaatsingen.
Er bestaan borden en beginposities van $n$ stukjes waarvoor werkelijk kwadratisch veel verplaatsingen nodig zijn. Dit is goed voor een puzzelontwerper om te weten. Je wil geen puzzel met honderden stukjes, want dan zijn misschien tienduizenden verplaatsingen nodig om de puzzel op te lossen, en dat kost uren.
Tenslotte denken we nog even na over die ene, vreemde uitzondering. Waarom lukt het niet om stukjes willekeurig te verplaatsen op het bord van de zespuntige ster?
Opgave 1Kleur de hexagonen van het bord van de zespuntige ster in drie kleuren zwart, grijs en wit, zodanig dat twee aangrenzende cellen nooit dezelfde kleur hebben. |
Merk op dat de kleuring in feite maar op een manier kan, al kan je hele kleuren omwisselen. Merk verder op dat het patroon van de kleuring uitgebreid kan worden naar een willekeurig groot bord. Het is een regelmatig, symmetrisch patroon. Laten we eens aannemen dat je voor de middelste cel de kleur grijs hebt genomen. Dan zullen ook de zes punten van de stervorm grijs zijn. De tussenliggende ring is afwisselend wit en zwart. Er zijn dus zeven grijze cellen, drie witte cellen en drie zwarte cellen.
Opgave 2Als we zes stukjes op het bord leggen, welke cellen kunnen allemaal leeg zijn? |
Er is dus altijd een grijze cel leeg, hoe de stukjes ook op het bord liggen. Na elke verplaatsing is weer een andere grijze cel leeg. De zwarte en witte cellen kunnen nooit leeg zijn, en dus kan een stukje dat een witte cel bedekt, nooit die witte cel loslaten. En datzelfde geldt voor zwart.
Het interessante is dat dit bord het enige bord is dat geen flessenhals heeft, geen afgesloten buitengebied, maar wel meer cellen in één van de kleuren dan van de andere twee kleuren samen.
Bron: Joep Hamersma, Marc van Kreveld, Yushi Uno, en Tom C. van der Zanden (2020), Gourds: a slidingblock puzzle with turning. 31st International Symposium on Algorithms and Computation (ISAAC 2020). Schloss Dagstuhl-Leibniz-Zentrum für Informatik, 2020. https://arxiv.org/pdf/2011.00968 |
