Elkaar succes wensen middels een ferme handdruk: of het nou helpt of niet, het is een sympathiek gebaar. Over handen schudden voorafgaand aan een examen ging de slotopgave van de tweede ronde van de Wiskunde Olympiade die op 11 maart plaatsvond:

Opgave C2 (NWO, Tweede ronde 2016) 

Studenten zitten in een zaal met tafeltjes in examenopstelling. Er zijn n rijen van m tafeltjes en alle tafeltjes zijn bezet. We weten bovendien dat $m\geq 3$ en dat $n\geq 3$. Studenten die direct achter elkaar, naast elkaar of diagonaal van elkaar zitten zijn buren. Studenten in het midden van de zaal hebben dus 8 buren. Voor aanvang van het examen schudt iedere student eenmaal de hand van al zijn buren. In totaal wordt er 1020 keer handen geschud. Bepaal het aantal studenten.

Voordat we gaan rekenen, zetten we de grote lijn uit. De opgave bestaat uit drie stappen:

Stap 1. Maak een vergelijking, waarin je het verband tussen $m,n$ en 1020 vastlegt. Krab daarbij even achter je oren, want er zit een beertje op de weg. Een vuistregel zegt namelijk dat je doorgaans bij twee onbekenden ook twee vergelijkingen nodig hebt, anders kan het gebeuren dat je oneindig veel oplossingen krijgt en dat is niet zo leuk. Een tweede vergelijking is dus misschien vereist.

Stap 2. Los deze vergelijking(en) op. Als het mee zit, levert dat $m$ en $n$ of eventueel alleen het product $mn$.

Stap 3. Geef antwoord op de gestelde vraag. Dat lijkt heel vanzelfsprekend, maar wordt helaas vaak vergeten.

STAP 1

We moeten ons eerst realiseren hoe handen schudden eigenlijk in zijn werk gaat. Je kunt iemand alleen een hand geven als de ander jou ook een hand geeft. Gelukkig maar, want anders zou je zomaar onthand kunnen raken. Als twee studenten elkaar een hand geven, wordt er één keer handen geschud. Verwar dit niet met ‘de hand reiken’, want dat is een eenzijdige actie, waarbij eigenlijk nog niets geschud wordt. Er wordt 1020 keer handen geschud. Dat betekent dat er 2040 keer door een kandidaat een hand wordt gegeven. 

We laten nu twee manieren zien waarop het aantal keer handen schudden uitgedrukt kan worden in $m$ en $n$.

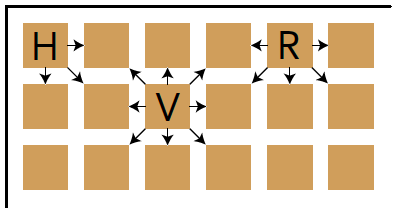
In figuur 1 zien we het handen schudden vanuit het gezichtspunt van de studenten. Er zijn hoekstudenten ($H$) die in de hoeken van de zaal zitten. Er zijn randstudenten ($R$) die aan de randen zitten, maar niet in de hoeken. En er zijn veldstudenten ($V$) die niet aan een rand zitten. In de tabel op pagina 23 zie je hoeveel er van deze soorten voorkomen en hoe vaak zij een hand geven. Een $H$-student geeft 3 keer een hand, een $R$-student 5 keer en een $V$-student 8 keer.

Zo komen we uit op $8mn – 6m – 6n + 4 = 2040$ en deze vergelijking is te herleiden tot

$$4mn-3m-3n=1018\ \ \ \ \ \ \ \ \ \ \  (1)$$ 

Maar we kunnen het ook bekijken vanuit de opstelling van de zaal. In figuur 2 zie je de tafeltjes als dikke stippen en elk verbindingslijntje stelt één keer handen schudden voor.

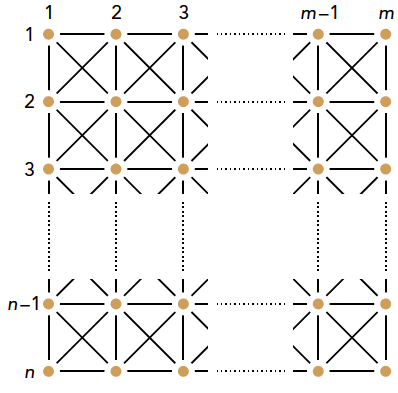
Er zijn $n$ rijen met elk $m$ tafeltjes. Elk verbindingslijntje tussen twee punten is één keer handen schudden. Er zijn $n(m – 1)$ horizontale verbindingen en $m(n – 1)$ verticale. Elk kruis betekent 2 verbindingen en er zijn $(m – 1)(n – 1)$ kruisen. Er zijn dus $n(m – 1) + m(n – 1) + 2(m – 1)(n – 1) = 4mn – 3m – 3n + 2$ verbindingen in totaal, dus $4mn – 3m – 3n + 2 = 1020$, oftewel $4mn – 3m – 3n = 1018$. Dat is (uiteraard) hetzelfde als wat we al eerder vonden.

STAP 2

Nu gaan we de gevonden vergelijking proberen op te lossen. Zoals we boven al vreesden, hebben we maar één vergelijking en dat is misschien niet genoeg, want dan bestaat het risico op oneindig veel oplossingen. Dat is hier inderdaad het geval. Laten we willekeurig maar wat proberen. Kies bijvoorbeeld $m = 10$. Invullen levert $4 \times 10 \times n - 3 \times 10 - 3 \times n = 1018 en als we dat oplossen, vinden we $n = 28\frac{12}{37}.

Aha! Dat is wiskundig wel een correcte oplossing, maar er bestaan gelukkig geen $\frac{12}{37}$ studenten. En daarmee hebben we dus meteen onze tweede eis te pakken, waar we dankbaar gebruik van gaan maken: $m$ en $n$ moeten natuurlijk gehele getallen zijn!

We gaan nu aan de slag met de ‘omgekeerde papegaaienbekmethode’ (zie het bovenstaande kader) om de vergelijking $4mn – 3m – 3n = 1018$ om te schrijven tot een factorisering, een vergelijking van de vorm $(2m + a)(2n + b) = d$. (We hadden ook voor een andere vorm zoals $(m + a)(4n + b) = d$ of $4(m + a)(n + b) = d$ kunnen kiezen; dat leidt uiteindelijk net zo goed tot vergelijking (2) hieronder.) Als we $(2m + a)(2n + b) = d$ uitwerken met de papegaaienbekmethode, staat er $4mn + 2bm + 2an + ab = d$, oftewel $4mn + 2bm + 2an = d – ab$.

soort	aantal studenten	aantal handen per student	aantal totaal gegeven handen
H	4	3	12
R	$2(m-2)+2(n-2) = 2m + 2n -8$	5	10m+10n-40
V	(m-2)(n-2) = mn -2m-2n+4	8	8mn-16m-16n+32
totaal	mn		8mn-6m-6n+4

 

We willen $a, b$ en $d$ zodanig kiezen dat hier in feite

gewoon de oorspronkelijke vergelijking $4mn – 3m - 3n = 1018$ staat. Dan moet er dus gelden dat $2b = -3$ en $2a = -3$ en $d - ab = 1018$. We vinden $a = -1\frac{1}{2}$ en $b = -1\frac{1}{2}$ en $d = 1018 + 2\frac{1}{4} = 1020\frac{1}{4}$. De op te lossen vergelijking wordt daarmee:

$$(2m-1\frac{1}{2})(2n-1\frac{1}{2})=1020\frac{1}{4},$$

waarbij $n$ en $m$ geheel zijn. Omdat we niet echt van breuken houden, vermenigvuldigen we beide kanten ten slotte met 4:

$$(4m – 3)(4n – 3) = 4081.\ \ \ \ \ \ \ \ \ (2)$$

 

Omdat we weten dat $m$ en $n$ gehele getallen zijn, komt het probleem er nu dus op neer om 4081 te schrijven als een product van twee gehele getallen. We leggen 4081 daarom even op de behandeltafel: we gaan hem ontbinden.

De ontbinding is handig te starten via de ‘1001-methode’ (zie het onderstaande kader): 4081 – 4004 = 77. Nu is 77 deelbaar door 7 en 11, dus hetzelfde geldt voor 4081. Na enig rekenwerk vinden we dat $4081 = 7 \times 11 \times 53$.

Omdat in dit probleem m en n verwisselbaar zijn, kunnen we ervoor kiezen dat $m \leq n$, zodat ook $4m – 3 \leq 4n – 3$. Daarmee blijven er vier opties over:

• $4m - 3=1$, dat levert $m=1$ en $n=1021$. Maar in het gegeven staat dat $m\geq 3$, dus die mogelijkheid vervalt.
• $4m-3=7$ levert geen gehele $m$.
• $4m-3=11$ levert ook geen gehele $m$.
• $4m-3 = 53$, jawel dat levert $m=14

(Het geval $4m – 3 = 77$ komt niet meer in aanmerking, want dan is $4m – 3 > 4n – 3$.)

Het geval $4m – 3 = 53$ komt overeen met $4n – 3 = 7 \times 11 = 77$ en dan is $n$ gelukkig ook geheel, namelijk $n = 20$. Dus we hebben hem!

Stap 3

Vergeet nu niet het antwoord te geven: er zijn $mn = 14 \times 20 = 280$ studenten. En kijk eens terug: waarom staat er in de opgave eigenlijk dat $m \geq 3$? We zagen toch onderweg dat $m = 1$ en $n = 1021$ (en dus $mn = 1021$) ook een oplossing was? Dat is inderdaad het geval, maar zie het even voor je. Dan hebben we een examen-‘zaal’ waarin 1021 studenten in één rij achter of naast elkaar zitten. Het examen zou dan bijvoorbeeld op een ongebruikte startbaan van een vliegveld moeten plaatsvinden en door surveillanten op een e-bike in de gaten moeten worden gehouden!

De 1001-methode over deelbaarheid door 7, 11 en 13

Als je wilt onderzoeken of een getal deelbaar is door 7, kun je er een (slim) veelvoud van 7 van aftrekken, want daarbij blijft de deelbaarheid behouden. Bijvoorbeeld: 203 - 63 =140, dus 203 is deelbaar door 7. Aan 682 - 42 = 640 kun je zien dat 682 niet deelbaar is door 7.

Omdat $7 \times 11 \times 13 = 1001$, kun je met 1001 drie vliegen in één klap slaan, want met veelvouden van 1001 kun je gemakkelijk rekenen. Demonstratie: we gaan $n = 293.527.108$ onderzoeken op deelbaarheid door 7, 11 en 13 door $n$ slim te verminderen (of eventueel te verhogen) met veelvouden van 1001.

Allereerst bekijken we 293.527.108 – 108.108 = 293.419.000. Die nullen aan het eind laten we weg, want die hebben toch geen invloed. Dan bekijken we bijvoorbeeld 293.419 – 293.293 = 126. Omdat 126 wel deelbaar is door 7 maar niet door 11 of 13, geldt datzelfde ook voor 293.527.108.