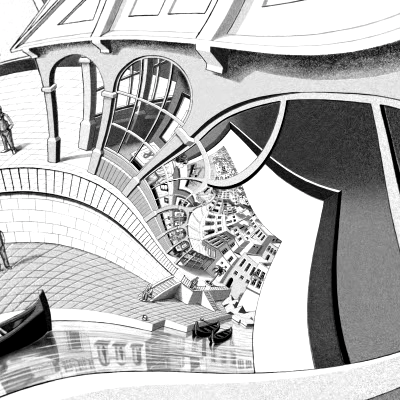
Maurits Cornelis Escher (1898 - 1972) voltooide zijn werk Prententoonstelling in 1956. Het is een van de meest ingewikkelde werken uit zijn oeuvre. Hij schrijft over zijn eigen verbazing in één van zijn brieven aan zijn zoon Arthur: "Zoiets raars heb ik, geloof ik, van mijn leven nog niet gemaakt." En: "Misschien ben ik niet ver verwijderd van Einsteins gekromde heelal!" Het lukte hem niet het werk helemaal af te maken. Hij liet een witte cirkel in het midden open en gebruikte dat voor de signering.

Waarom is Prentententoonstelling zo'n fascinerende voorstelling? Je ziet in figuur 1 de reconstructie (dus de complete versie) van de Universiteit Leiden uit 2002. Verplaats je eens in de jongeman links op de voorgrond. Wat ziet hij? Een schilderij van een boot en een wat huizen aan het water. Aan de linkerkant is het passe-partout goed zichtbaar. Maar hé, wat gebeurt er rechts op dat schilderij? De gebouwen lijken uit het schilderij te stappen. In een van de gebouwen leunt een vrouw uit het raam. En in dat gebouw is een prentententoonstelling en staat helemaal links een bezoeker, dezelfde jongeman. Wat ziet hij? Enzovoorts. 

In 2002 – maar liefst 56 jaar na de voltooiing van Prentententoonstelling – werd de wereld van de kunst en de wiskunde opgeschud. Het was een groep wiskundigen onder leiding van Hendrik Lenstra en Bart de Smit van de Universiteit Leiden gelukt het gat in het midden van de Prentententoonstelling in te vullen. Ze ontdekten de wiskundige afbeeldingsformule die achter de prent schuilging. Ze hebben er zo’n twee jaar aan gewerkt. 

Niet alleen om de formule te ontdekken, maar ook om de originele onvervormde prent te reconstrueren. Daarbij werd de hulp van illustrator Jacqueline Hofstra ingeroepen om ontbrekende stukken in te laten vullen. 

En wat staat er in dat witte gat, vraag je je natuurlijk af. Daar staat de complete voorstelling opnieuw, maar wel geroteerd en sterk verkleind. En je begrijpt het waarschijnlijk al, in dat middelpunt staat het werk nog een keer. Weer geroteerd en nog verder verkleind. Er ontstaat een soort van draaikolk, met daarin het Droste-effect. Zie in figuur 2 wordt steeds verder ingezoomd in het middelpunt.

$\color{White}{Figuur\ 2}$

Zebra-boekje nr. 60

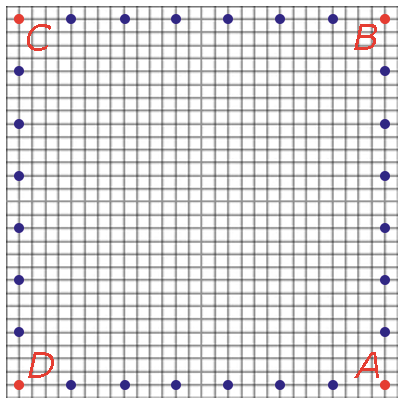
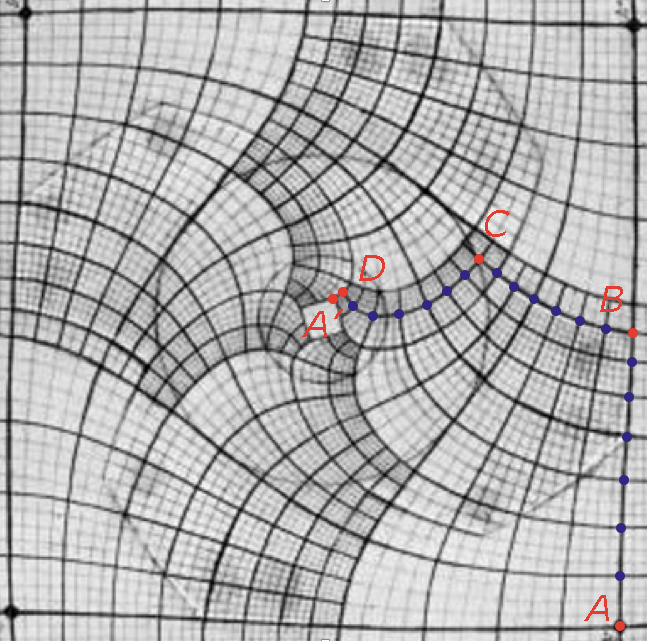
Het inzichtelijk maken van de wiskundige principes achter de 'transformatie' is niet eenvoudig. Afgelopen jaar – bijna 20 jaar na de ontdekking van de formule – verscheen de Zebra-uitgave Verdwijnpunt Prentententoonstelling van M. C. Escher opgelost. Rick Vooys, docent wiskunde en natuurkunde, neemt je stap voor stap mee in de transformatie. De oorspronkelijke afbeelding (die uiteindelijk door reconstructie is achterhaald) is Prentenvoorstelling getekend in een 'recht rooster'.  Escher ontwierp voor zijn weergave een eigen rooster (zie figuur 3). Vergelijk de roosters eens. Als je de route $ABCD$ doorloopt in het rechte rooster, doorloop je een vierkant. In het Escherrooster worden de afstanden steeds korter. Je komt
bovendien niet terug bij $A$ uit, maar bij $A^\prime$. 

Je ziet hoe het Droste-effect optreedt. Een kopie van punt $A$ vind je terug in het midden. Wat je misschien ook opvalt is dat de lijnen in zowel het rechte rooster als in het Escherrooster elkaar loodrecht snijden. Hoeken worden dus niet vervormd in het Escherrooster. Dit principe heet 'conformiteit' in de wiskunde en speelt ook een belangrijke rol in de cartografie. 

De roosters vormen ook de basis voor het ontdekken van de formule die erachter schuil gaat. In het boekje word je stap voor stap daarin meegenomen, zodat je uiteindelijk de exacte waarden van de vergrotingsfactor en de rotatiehoek vindt. Hierbij komt vooral het afbeelden van complexe getallen van pas. De ingewikkelde stappen worden in het Zebraboekje inzichtelijk gemaakt met 'behangpapier' dat je kunt oprollen tot een koker. Weet je de formule van het rechte rooster naar het Escherrooster, dan kun je met de inverse formule de originele prent in het rechte rooster reconstrueren. 

Al het werk van de Universiteit Leiden uit 2002 is nog altijd te vinden op escherdroste.math.leidenuniv.nl. Je kunt er diverse animaties downloaden die het Droste-effect van Prententoonstelling tot leven laten komen. Een tip: zet je speler niet op 'herhalen'. Je blijft er anders eindeloos naar kijken…

		Het Droste-effect is een klassieker uit de wereld van de vormgeving. Een dame serveert op een dienblaadje een kopje chocolademelk met een pak cacao ernaast. Met op dat pak dezelfde dame met hetzelfde dienblaadje met een kop choco en ook weer een pak Droste ernaast. Enzovoorts. Je ziet dat het plaatje telkens verkleind terugkomt. Na twee keer verkleinen zie je het pak al bijna niet meer.

 

		Pythagoras mag 3 exemplaren van dit boek verloten! Stuur voor 1 september 2021 een mailtje naar  [email protected] en misschien win jij  dit Zebraboekje!