Ik heb met twee binnenbanden een experiment gedaan, waarbij ik ze telkens verder oppompte en $d$ en $D$ opmat. Bij de eerste (I) hield ik er al mee op toen de buis krap twee keer zo dik geworden was. Ik had namelijk geen idee hoeveel druk een losse binnenband kan hebben zonder uit elkaar te klappen (zie figuur 1).

Bij de tweede binnenband (II) had ik voor een veiligheidsbril en gehoorbescherming gezorgd, en ben ik doorgegaan met pompen tot de band op pompslag 63 met een heidense knal explodeerde. Heel merkwaardig is, dat de band op twee plekken tegelijk barstte, zodat er twee losse stukken ontstonden.

We gaan nu eerst proberen theoretisch te voorspellen hoe een binnenband oppompt, en toetsen op het eind van dit artikel de theorie aan het experiment.

Krachten in evenwicht

Heel in het algemeen geldt, dat de luchtdruk $\rm P$ in de band tegen het rubber drukt. Daardoor rekt dit uit, wat een tegenkracht in het rubber opwekt. Hoe meer uitrekking, hoe meer rekkracht, totdat alle krachten in de band bij zekere $D$ en $d$ in evenwicht zijn met $\rm P$.

Omdat de druk door een gas (lucht) wordt geleverd, is $\rm P$ overal hetzelfde, en werkt die overal loodrecht op het rubber oppervlak (als dit niet zo was, zou er spontaan gas gaan stromen totdat het wel zo was).

Bij nader inzien lijkt dit de situatie juist erg gecompliceerd te maken. Immers, in elk punt staat de luchtdruk loodrecht op de rubberen wand, maar de rekkracht in het dunne rubber is parallel aan de wand, dus loodrecht op de luchtdruk. Hoe kunnen die elkaar dan ooit in evenwicht houden? Een kracht en een kracht loodrecht daarop zijn opgeteld immers nooit samen $0$.

In feite zorgt de kromming van de wand ervoor, dat er in elk stukje rubber ook een component van de rekkracht loodrecht op de wand staat die de luchtdruk in bedwang houdt. Maar we gaan het oprekken van de torus niet stukje voor stukje van de rubberen wand becijferen.

In plaats daarvan gaan we de torus twee keer handig 'aansnijden', en rekenen we de krachten op de snijvlakken uit.

Het oprekken van de ring

Eerst doorsnijden we de torus met een denkbeeldig vlak loodrecht op de buis (zie figuur 2).

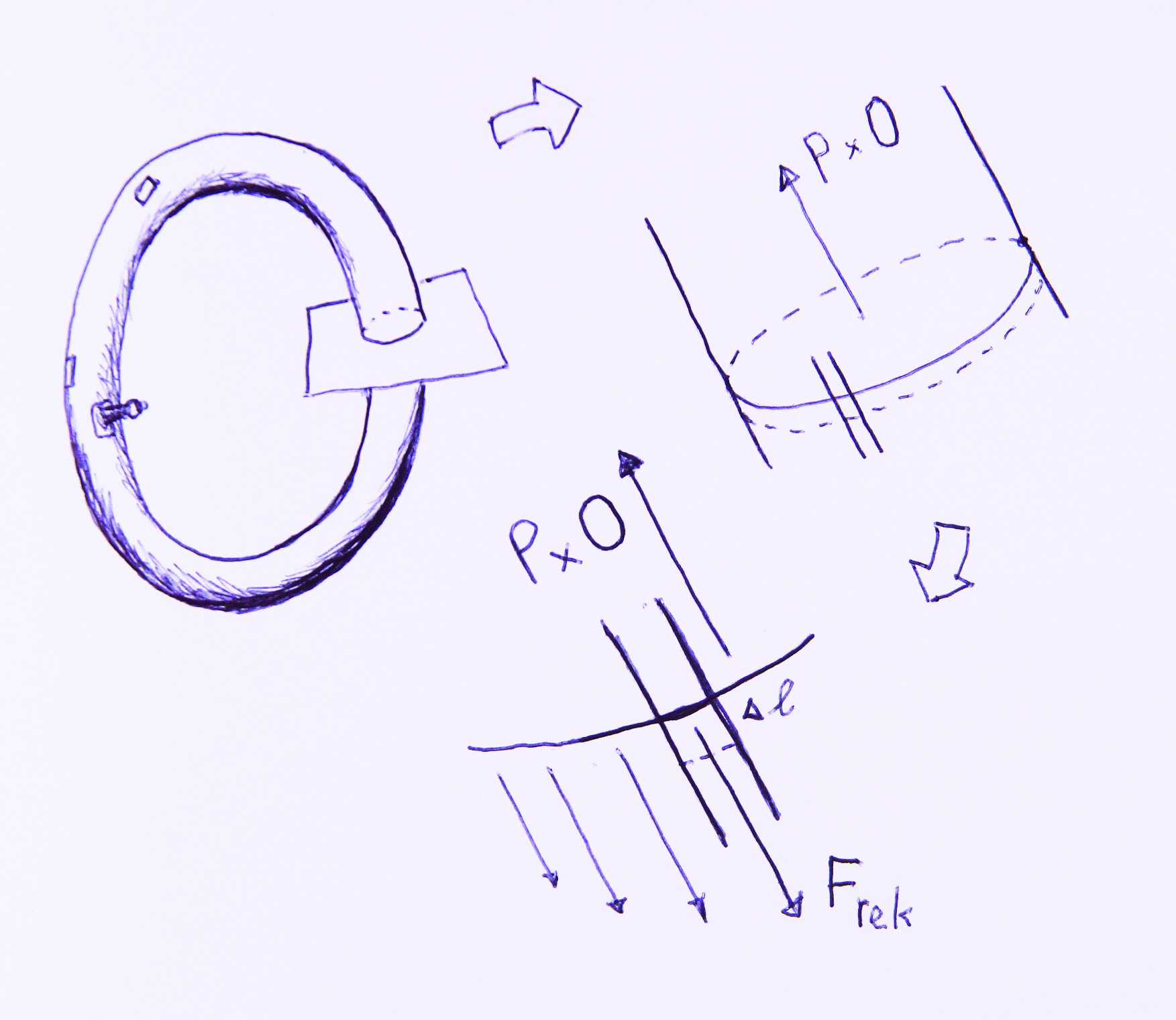
Als hier echt een luchtdicht vlak door de buis ging, zou de luchtdruk $\rm P$ de twee uiteinden uit elkaar drukken met een kracht $\rm P \times O$, met ${\rm O} = \pi/4 \times d^2$, de dwarsdoorsnede van de band.

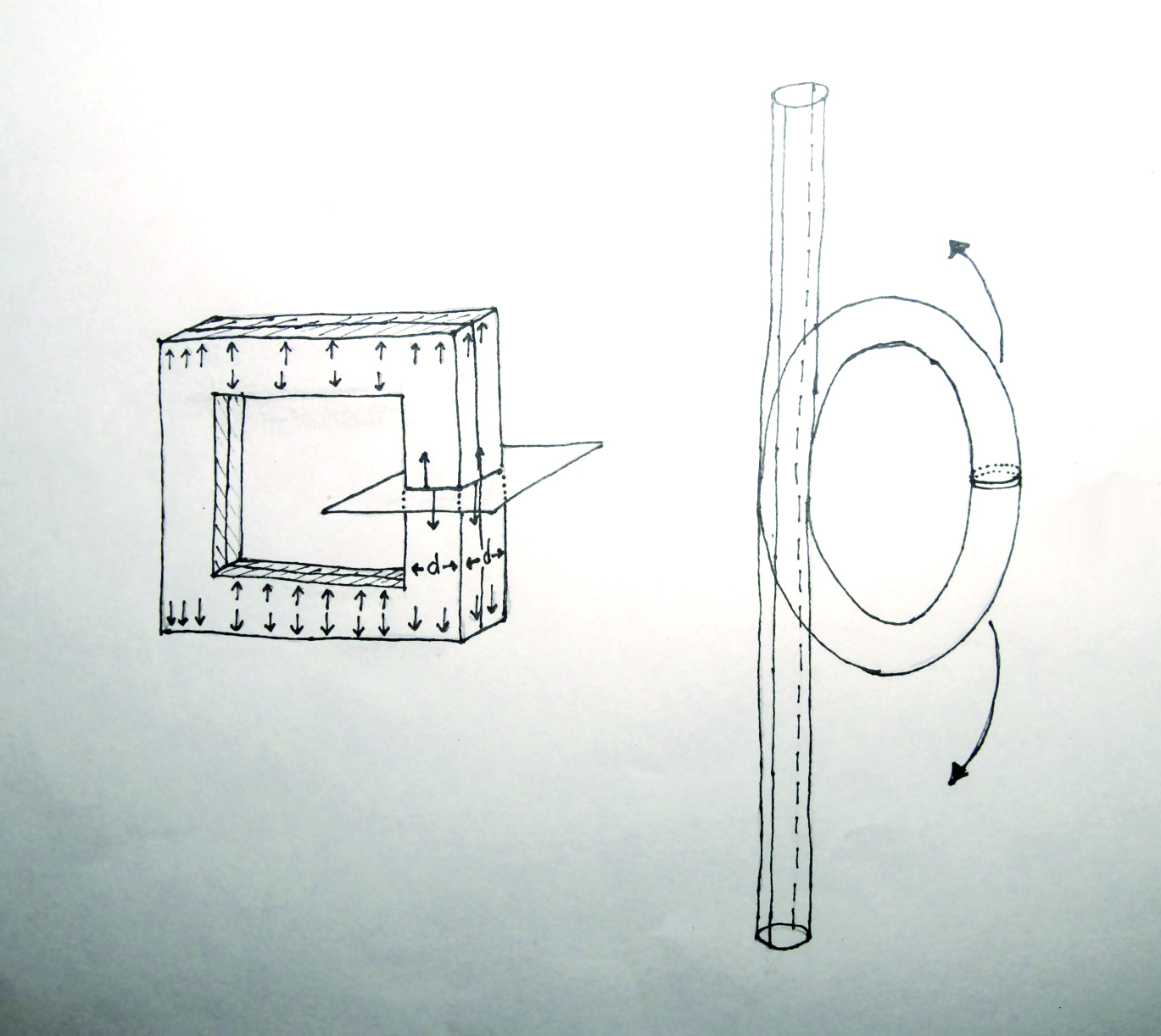
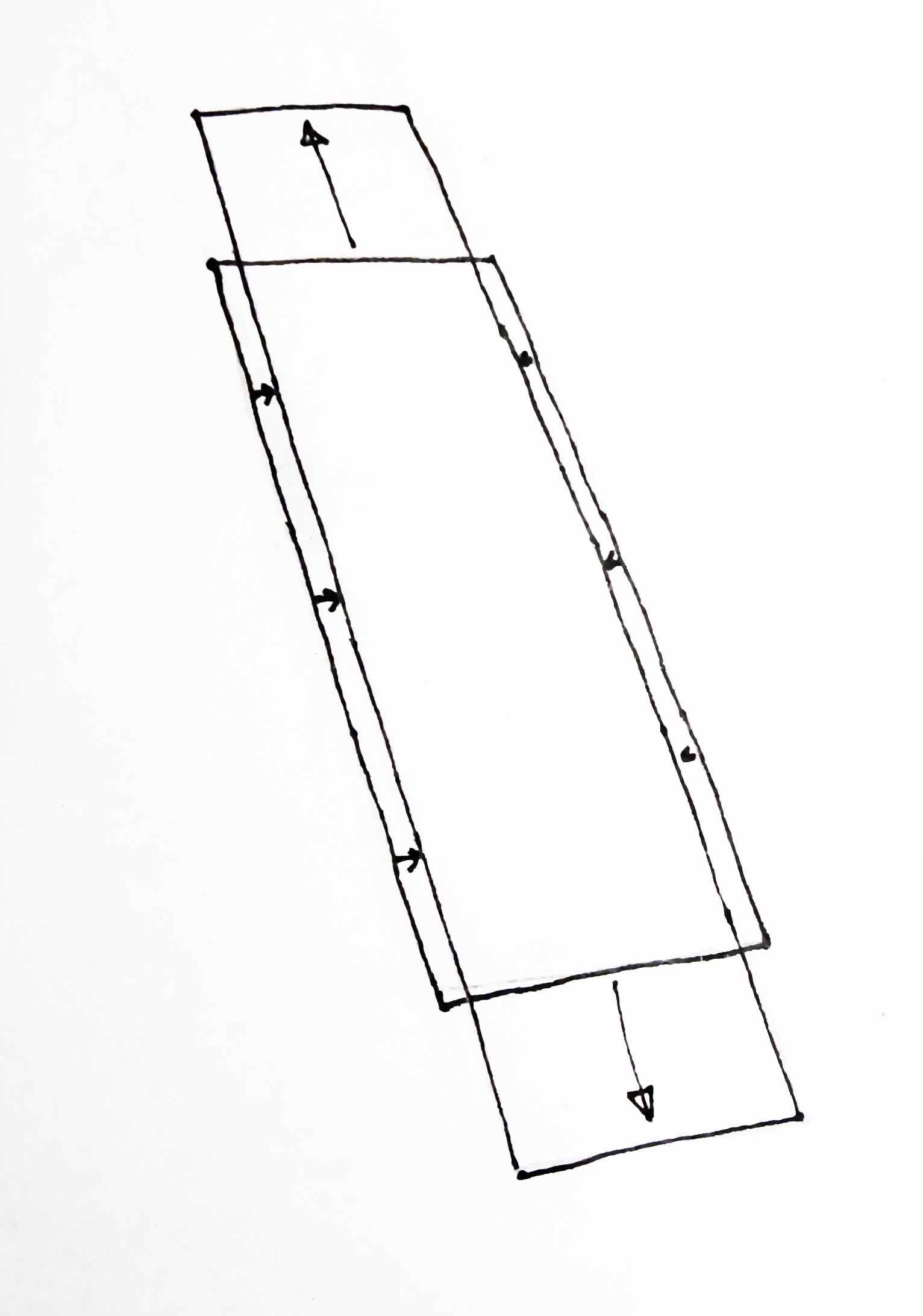
Als je niet meteen inziet waarom het zinnig is om zo'n snijvlak te kiezen, kun je in gedachten de torus vervangen door een vierkante torus als in figuur 3. De pijltjes geven aan hoe de luchtdruk op de binnenwand werkt (alleen de verticale componenten zijn getekend). De pijltjes naar boven en naar beneden heffen elkaar overal op waar de vierkante torus niet doorsneden is.

Maar op het snijvlak zal de luchtdruk $\rm P$ de twee helften uit elkaar willen duwen met  een kracht ${\rm P \times O = P} \times d^2$. In de ronde torus is de netto kracht die het rubber in de lengterichting  van de buis uit elkaar trekt eveneens $\rm P \times O$.

Nog een andere manier om je dit voor te stellen is, dat je de torus echt doorsnijdt en uitvouwt tot een rechte buis (een cilinder) met lengte $\pi D$. De luchtdruk tegen de uiteinden zal dan de buis uit elkaar willen trekken met dezelfde kracht $\rm P \times O$.

De luchtdruk moet gecompenseerd worden door de rekkracht van het rubber in de band. We definiëren nu $\rm f$, de rekkracht van het rubber per mm breedte van de buis. Let wel, $\rm f$ is geen constante, maar daar komen we zo meteen op terug. De totale rekkracht in de lengterichting van de buis is ${\rm f} \times \pi d$, met $\pi d$ de omtrek van de band.

Op het moment dat de band niet verder opgepompt wordt, is er evenwicht tussen alle krachten.

Dus:

${\rm F_{lucht} = P}\times \pi/4\times d^2$

$(1)$

en

${\rm F_{rek} = f} \times \pi d$

$(2)$

Nu nemen we voor de rekkracht aan dat die net zo werkt als een veer die je uitrekt: $\rm f$ is dan evenredig aan de uitrekking $\Delta \ell : {\rm f} = f \times \Delta \ell$, met $f$ het equivalent van de veerconstante voor een strookje rubber (dit is de wet van Hooke).

Echter, die veerconstante is weer omgekeerd evenredig met de totale beginlengte van het rubber dat uitgerekt wordt (hoe langer de strook rubber, hoe makkelijker het is om hem $1$ millimeter uit te rekken): $f = {\rm C}/\ell_0$. $\rm C$ is een constante, die iets zegt over hoe rekbaar het rubber van deze band is.

De relatie $f={\rm C}/\ell_0$ zullen we straks, bij de tweede doorsnijding van de band, opnieuw gebruiken, maar dan is $\ell_0$ anders. Hier is $\ell_0 = \pi D_0$, want de luchtdruk rekt de diameter $D$ van de band op vanaf $D_0$, de diameter van de band bij druk $0$.

We hadden al ${\rm f} = f \times\Delta\ell$, dus

$${\rm f = C}/\pi D_0\times\Delta\ell.$$

Voor de totale rekkracht $\rm F_{rek}$ in de lengterichting levert dit op:

${\rm F_{rek}=f}\times\pi d = {\rm C}/\pi D_0\times\Delta\ell\times\pi d={\rm C}/D_0\times\Delta\ell\times d$

$(3)$

Stel $(1)$ en $(3)$ aan elkaar gelijk:

${\rm F_{lucht} = F_{rek}}$ hieruit volgt ${\rm P}\times\pi/4\times d^2={\rm C}/D_0\times\Delta\ell\times d$ dus ${\rm P = 4C}\times\Delta\ell/(\pi D_0d)$

en als we ook nog schrijven $\Delta\ell=\pi\Delta D$ wordt dit:

${\rm P = 4C}\times\Delta D/(D_0 d)$

$(4)$

Het oprekken van de buisdikte

Vervolgens berekenen we de krachten als gevolg van het oprekken van de buisdikte. Als we een vlak door het midden van de buis nemen, (zie figuur 4) werkt de luchtdruk aan beide zijden loodrecht op dat vlak met een kracht:

${\rm F_{lucht}=P}\times k\times d.$

$(5)$

Deze kracht wordt gecompenseerd door de rekkracht in het rubber langs beide zijkanten van de buis, dus over een totale lengte $2k$.

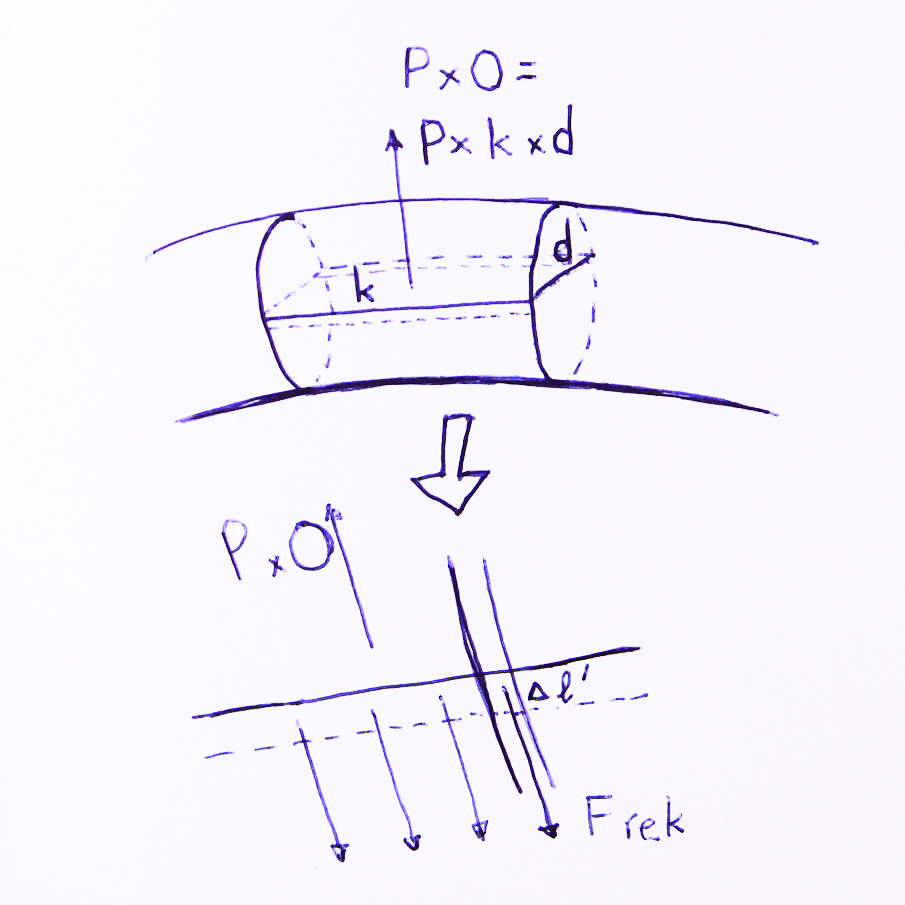
(In het beeld waarin de torus echt is doorgesneden en uitgevouwen tot een cilinder met lengte $\pi D_0$, kun je je ook voorstellen dat je de hele cilinder over de lengte doormidden snijdt. De lengte $2k$ wordt dan $2\pi D_0$, zie opnieuw figuur 3)

${\rm F_{rek}=f}\times 2k$

$(6)$

we schrijven weer ${\rm f = f}^{\prime}\times \Delta\ell^{\prime} = {\rm C}/\Delta\ell^{\prime}_0\times \Delta\ell^{\prime}$ waarbij $\Delta\ell^{\prime}$ en $\ell^{\prime}_0$ de uitrekking en de beginlengte zijn van een flinterdun strookje rubber dat rondom de buis loopt. Omdat $\Delta\ell^{\prime}=\pi\times\Delta d$  en $\ell^{\prime}_0=\pi\times d_0$, wordt dit:

${\rm F_{rek} = C}\times\Delta d/d_0\times 2k$

$(7)$

stel $(5)$ en $(7)$  aan elkaar gelijk:

	$\rm F_{lucht}=F_{rek}$ oftewel
	${\rm P}\times k\times d = {\rm C} \times\Delta d/d_0\times 2k$ dus
	${\rm P = 2C}\times\Delta d/(d\times d_0)$	$(8)$

We hebben nu de druk $\rm P$ uitgerekend op basis van de krachten in de lengte, en daarna op basis van de krachten in de breedte van de band. Die $\rm P$ moet natuurlijk in beide gevallen hetzelfde zijn, want een gas kan niet in de ene richting een andere druk uitoefenen dat een andere, dus $(4) = (8)$:

	$4{\rm C}\times \Delta D/(D_0d)=2{\rm C}\times \Delta d/(d_0\times d)$ dus
	$2\Delta D/D_0=\Delta d/d_0$	$(9)$

Het mooie is, dat de constante $\rm C$ is weggevallen; wat overblijft is een simpele uitdrukking voor de relatieve uitrekkingen van de torus wat betreft $D$ en $d$. Een grafiek van $D$ tegen $d$ zou een rechte lijn op moeten leveren.

Als de buisdikte en de diameter van de band relatief evenveel toe nemen, zou gewoon gelden: $\Delta D/D_0 = \Delta d/d_0$. De factor $2$ is het gevolg van de topologie van de torus, waarbij je onder topologie moet verstaan: die aspecten van de vorm die juist niet beïnvloed worden door het oppompen, of door de verhouding tussen $d$ en $D$.

Je kan je afvragen: waarom juist deze twee aansnijdingen van de torus? De reden is, dat in een torus alleen op deze twee snijvlakken de rekkracht overal in het rubber loodrecht op het snijvlak staat. Alleen daarom mag je de totale rekkracht gelijk stellen aan de druk maal de oppervlakte van de doorsnijding. Dat levert een veel simpeler berekening op, dan als je afzonderlijk rekening moet houden met componenten van de rekkracht loodrecht op, en parallel aan het snijvlak.

Toetsing aan de realiteit

Tot zover de theorie, maar klopt het ook met het experiment? De metingen leverden de grafiek in figuur 5 op.

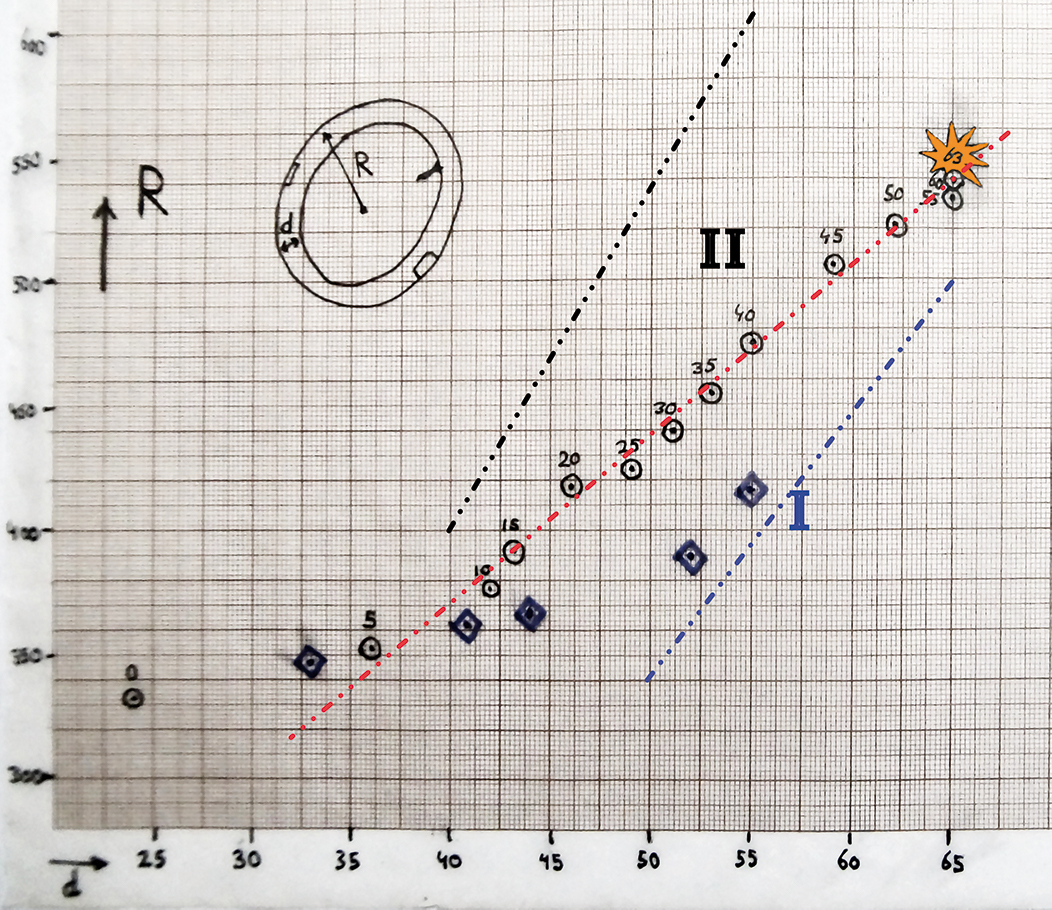
De blauwe ruitjes zijn binnenband I, de zwarte cirkeltjes binnenband II.

We zien meteen dat er nogal wat verschil is tussen de twee binnenbanden. In hoeverre dit strookt met de theorie gaan we nu na.

Uit $(9)$ volgt:

$2\Delta D/D_0=\Delta d/d_0$\ dus $\Delta D=(D_0/2d_0)\times \Delta d$

We bekijken voor beide binnenbanden de factor $(D_0/2d_0)$, de richtingscoëfficiënt (helling) van de hypothetische rechte lijn door de meetpunten.

Binnenband I

Als je invult $d_0=33$ en $D_0=2R_0=694$ (de afmetingen van de torus, in millimeter, toen er net voldoende lucht in zat om hem vorm te laten krijgen), wordt de helling:

$(D_0/2d_0)=10{,}5$

Dus voor iedere millimeter dat de buis dikker wordt, zou de diameter van de ring $10{,}5$ millimeter toe moeten nemen. Dit is de blauwe stippellijn in de grafiek, met richtingscoëfficiënt $10{,}5$.

In het begin klopt dit niet. Pas de twee laatste metingen suggereren dat de binnenband zich houdt aan het theoretisch afgeleide verband.

Binnenband II

Als je als beginafmetingen invult $d_0=24$ en $D_0=2R_0=664$ wordt de helling:

$(D_0/2d_0) = 13{,}8$

De zwarte stippellijn in de grafiek heeft richtingscoëfficiënt $13{,}8$. De metingen laten, na een aarzelende start, inderdaad een vrij overtuigende rechte lijn zien. De rode stippellijn is met een timmermansoog zo goed mogelijk door de meetpunten getrokken, (met verwaarlozing van het eerste meetpunt). De helling van deze lijn is ongeveer: 

$\Delta D/\Delta d=6{,}6$

De meest dubieuze aanname

De overeenstemming tussen theorie en experiment is dus maar pover. Binnenband I levert geen rechte lijn voor $D$ als functie van $d$ op, mogelijk omdat die niet ver genoeg is opgepompt. Voor binnenband II is er wel een rechte lijn in de grafiek, maar zou de 'topologische' factor $2$ eerder $4$ moeten zijn, om een waarde voor $(D_0/2d_0)$ van $6{,}6$ te krijgen.

Welke aanname in de berekening is het meest dubieus? Vrijwel zeker, dat een stuk rubber net zo uitrekt als een ideale veer. In feite zal een strookje rubber dat je in de lengte uitrekt, in breedte afnemen (zie figuur 6).

Voor een strook rubber met lengte $L$ en breedte $B$ die in de lengterichting wordt uitgerekt geldt de Poissonfactor $v$:

$\Delta B/B = v \times \Delta L/L$

Uit experimenten blijkt dat $v$ voor rubber ongeveer $1/2$ is: als je de strook in de lengterichting $10\%$ oprekt, wordt de breedte ongeveer $5\%$ minder. $(*)$

Dus als je een buis van rubber in de lengte uitrekt – niet door hem op te pompen, maar door een kracht van buitenaf - zal de diameter afnemen. Voor het oppompen van een binnenband betekent dit, dat je de uitrekking in de lengterichting, diameter $D$, niet onafhankelijk kunt zien van de uitrekking van de buisdiameter $d$, zoals in de afleiding boven wel gedaan is. Zodra de luchtdruk in de band toeneemt en $D$ gaat groeien, zal die luchtdruk tegelijkertijd de afname van $d$ teniet moeten doen.

Ik vermoed dat je dit niet meer in rekening kunt brengen in een statisch model met twee 'aansnijdingen' van de torus. Je ontkomt er dan niet aan om gekoppelde differentiaalvergelijkingen op te stellen voor de oprekking van een rubber torus. Dan worden de berekeningen veel gecompliceerder, en is als het ware het leuke er wel af.

Om echt te begrijpen hoe een torus die wordt opgepompt zich gedraagt, zouden zowel de experimenten als het model geavanceerder moeten zijn. De belangrijkste boodschap van bovenstaande berekeningen is eigenlijk, dat een torus niet uniform opzwelt als hij wordt opgepompt, en dat de topologie van de torus hierbij een belangrijke factor is. We mogen wel aannemen, dat dit ook voor allerlei andere ruimtelijke vormen geldt. Alleen een bol kan uniform opzwellen en een bol blijven, omdat die volkomen symmetrisch is.

$(*)$ Met dank aan Pythagoras-redacteur Jan Guichelaar, die me wees op het verstorend effect dat dit moet hebben op mijn model voor de rubber torus. Hij kon op theoretische wijze een Poissonfactor van exact $1/2$ afleiden, door aan te nemen dat het rubber bestaat uit een $2$-dimensionaal netwerk van atomen die aantrekkende krachten op elkaar uitoefenen waarvoor een veerconstante geldt.