Een fietswiel is opgebouwd uit drie onderdelen: een velg, een naaf en spaken. De buitenband en binnenband liggen om de velg en de naaf zit in het midden van het wiel. De spaken verbinden de naaf met de velg. Aan het ene eind van de spaak zit een kop. Net voor de kop maakt de spaak een hoek van 90 graden. Zo kan de spaak in de naaf worden 'gehaakt' Aan het andere uiteinde heeft de spaak ca. 1 cm schroefdraad, waar een nippel op wordt geschroefd. Met de nippel wordt de spaak in het wiel vastgezet. De kunst is de nippels zo vast te zetten, dat de spaak voldoende strak staat en de velg niet slingert als het wiel draait.

Het aantal spaken in fietswielen varieert, maar is altijd een veelvoud van vier. In een stadsfiets is 36 spaken het meest voorkomend, al komt 32 ook voor. En in fietsen met kleine wielen (kinderfietsen/vouwfietsen) zie je ook wel 20-spaakswielen. In fietsen voor zware toepassingen (bakfiets, tandem) zitten soms 48-spaakswielen. Je kunt elke naaf en velg met elk combineren, als ze allebei maar evenveel gaten hebben. Bij een naaf zijn de gaten verdeeld over beide kanten. De gaten zijn versprongen tegenover elkaar.

Op de foto hierboven zie je het vlechtpatroon van dichtbij bekeken. Spaken worden om en om met de kop naar binnen en naar buiten door de flens gehaakt. Deze naaf heeft 36 gaten. De 18 gaten in beide flenzen zijn versprongen ten opzichte van elkaar (zie de stippellijntjes). De diametrale afstand (d) tussen het midden van twee spaakgaten is essentieel voor het berekenen van de spaaklengte.

Spaakpatronen

Meest voor de hand liggend is om de naaf via de kortste weg met de velg te verbinden. Dit heet ook wel ‘radiaal gespaakt’. Spaken worden in dit patroon erg zwaar belast, met grote kans op spaakbreuk. Bij een tangentiaal spaakpatroon steken de spaken schuin van naaf naar velg over. Hierbij worden de krachten beter over de spaken verdeeld en breken ze minder gauw.

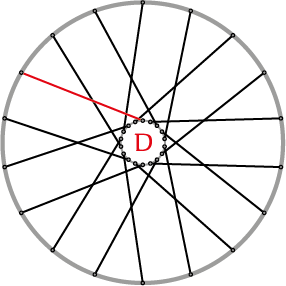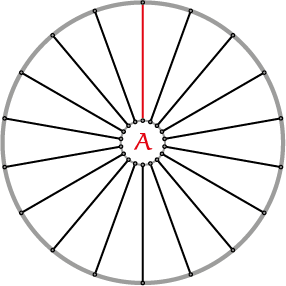
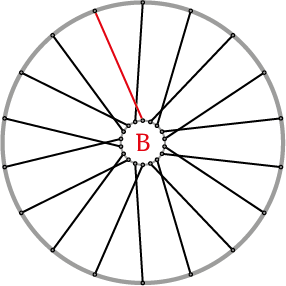
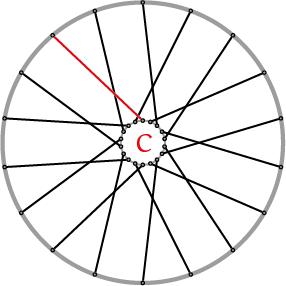
Schema 1 A Radiaal gespaakt (geen kruisingen); B Kruis over 1 (de rode spaak kruist 1 andere spaak); C Kruis over 2 (de rode spaak kruist 2 andere spaken); D Kruis over 3 (de rode spaak kruist 3 andere spaken)

Hierboven zie je schematisch vier spaakpatronen voor een 36-spaaks wiel. Je ziet hoe de 18 spaken aan een kant van het wiel van naaf naar velg lopen. Meestal is het spaakpatroon aan beide kanten van het wiel hetzelfde, maar dat hoeft niet per sé. Je kunt een patroon herkennen door te kijken naar hoeveel spaken een spaak onderweg kruist van naaf naar velg. In jargon zeggen fietsenmakers ‘kruis over 3’. Dat betekent dus dat een spaak drie andere kruist. Dit is het meest voorkomende patroon in stadsfietsen. Check het maar bij je eigen fiets.

De spaaklengte is behalve van het spaakpatroon ook nog afhankelijk van de flens van de naaf: hoe verder die flens van het midden staat, hoe schuiner de spaak loopt. Op de foto hiernaast is de flensafstand aangegeven met $a$, hier 20 mm.

Spaaklengte berekenen

Nu over naar de wiskunde. De vraag is: hoe groot is de afstand van het midden van het spaakgat in de naaf, tot aan de binnenkant van de velg. Deze afstand noemen we $L$. Als je deze lengte weet, kun je met een paar aanvullende gegevens de benodigde  spaaklengte berekenen.

De spaaklengte $L$ hangt af van de volgende gegevens:

• de diametrale afstand tussen de gaten van de naaf. Deze diameter noemen we $d$ en de bijbehorende straal $r$. 
• de  binnendiameter van de velg $D$ en straal $R$. 
• de afstand $a$ van flens naar het midden. 
• het gekozen spaakpatroon (met aantal kruisingen $k$). 
• het aantal spaken $n$ in het wiel. 

We gaan op zoek naar een formule waarbij we $L$ vinden door $r$, $R$, $a$, $k$ en $n$ in tevullen. We gaan daarbij stapsgewijs te werk. Eerst bekijken we een eenvoudigere situatie. We gaan er eerst even vanuit dat de spaken in één plat vlak liggen. We hoeven dan met $a$ nog even geen rekening te houden.

Opgave Wat is de spaaklengte van een plat radiaal gespaakt wiel zoals in het schema op de vorige pagina?

We gaan nu $L$ berekenen voor een 36-spaaks wiel met spaakpatroon kruis over 3. Omdat we in het platte vlak werken, noemen deze lengte $L_p$.

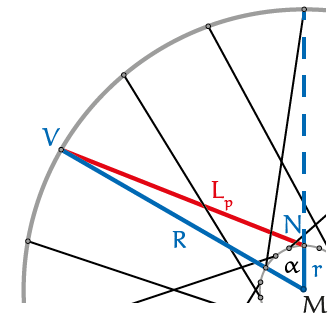In de figuur rechts tekenen we twee hulplijnen vanuit het middelpunt $M$ van het wiel. De ene hulplijn gaat naar het begin van
de spaak in het naafgat $N$ en trekken we door naar de velg. De andere lijn gaat naar het einde van de spaak in het velggat $V$. Vanwege de symmetrie van het spaakpatroon gaan beide lijnen door zowel een naafgat als een gat van de velg. De hoek tussen de beide hulplijnen kunnen we nu uitrekenen. Er zijn $1$8 spaakgaten. De hoek tussen 2 spaakgaten is dus $360^{\rm o} : 18 = 20^{\rm o}$ De hoek $\alpha$ tussen de twee hulplijnen is dus $60^{\rm o}$. In driehoek $MNV$ kunnen we nu met de cosinusregel kunnen we nu de spaaklengte $L_p$ uitrekenen. Er geldt:

$L^2=R^2+r^2-2Rr\cdot\cos(\alpha)$ met $\alpha=60^{\rm o}$.

Aangezien $\cos(60^{\rm o} = \tfrac{1}{2}$ geldt dus in deze situatie

$$L_p=\sqrt{R^2+r^2-Rr}.$$

We gaan nu kijken wat er aan de hand is in de werkelijke situatie, namelijk dat de spaken niet in één vlak liggen.

Op de foto links is $N$ het naafgat en $V$ het velggat. $L$ kan in deze rechthoekige driehoek worden berekend met Pythagoras:

$$L^2=a^2+L^2_p.$$

Door de eerder gevonden uitdrukking voor $L_p$ in te vullen en vervolgens links en rechts de wortel te trekken vinden we formule:

$$L=\sqrt{a^2+R^2+r^2-Rr}.$$

Deze formule geldt dus voor een 36-spaaks wiel met spaakpatroon kruis over 3.

Om de formule te veralgemeniseren kijken we allereerst naar het aantal spaken. Bij een spaakpatroon aan één kant van het wiel is de helft van het aantal spaken betrokken. De hoek tussen $2$ spaakgaten is bij $n$ spaken gelijk aan $360^{\rm o} : 0{,}5n = 720^{\rm o} : n$. We zagen dat we bij kruis over 3 deze hoek met $3$ moesten vermenigvuldigen. Die $3$ is niet toevallig gelijk aan het aantal kruisingen. Je kunt in schema 1 nagaan dat voor de andere spaakpatronen de hoek tussen twee spaakgaten met resp. $0$, $1$ en $2$ moet worden vermenigvuldigd. En dus wordt de algemene formule:

$$L=\sqrt{a^2+R^2+r^2-2Rr\cdot\cos\left(\frac{k}{n}\cdot 720^{\rm o}\right)}.$$

Millimeterwerk

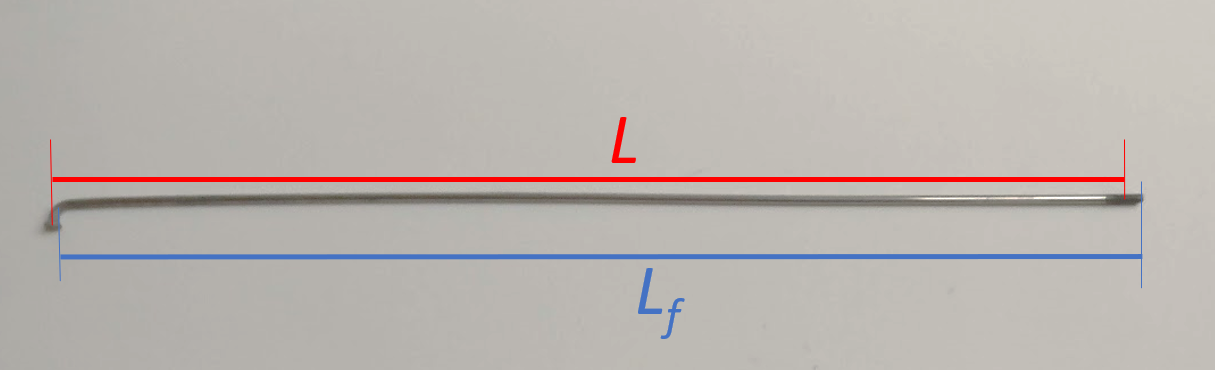
Nu kun je exact de lengte van de spaak berekenen. Om de spaaklengte te berekenen moet er dan nog alleen een aantal millimeter bij worden opgeteld. Dit aantal is afhankelijk van de dikte van de velg en het soort nippels dat wordt gebruikt. In de praktijk gaat het meestal om ongeveer 4 mm. Verder is er nog klein verschil bij de kop van de spaak: bij de formule reken je lengte $L$ vanaf het midden van spaakgat in de naaf.

De spaaklengte in de fietsvakhandel $L_f$ is echter de lengte tot aan de rand van het spaakgat (diameter is circa 2 mm). Bij het berekenen van de benodigde spaaklengte, haal je dus de halve diameter (circa 1 mm) af.

En dan nog een praktisch punt: spaken zijn niet in alle lengten verkrijgbaar. Tussen 8 en 30 cm loopt de lengte in stapjes van 2 mm op.