In Wie is de mol? moeten negen kandidaten de ene mol in hun midden ontmaskeren. Aan het eind van iedere aflevering vullen alle kandidaten een test in over wie ze denken dat de mol is. Degene die het minst weet van de mol, valt af, en de volgende aflevering heeft dus een kandidaat minder. In de laatste aflevering wint de persoon die het meest van de mol weet. Hoeveel mensen de mol weten te ontmaskeren hangt natuurlijk heel erg af van de kwaliteit van de mol en van de oplettendheid van de andere kandidaten. Maar grotendeels is het ontcijferen van de mol gewoon wiskunde!

Hoe goed is een slechte mol?

Stel dat je alleen maar heel domme kandidaten hebt. Ze zijn zo druk met opdrachten maken en met zichzelf verdacht maken, dat niemand eigenlijk een idee heeft wie de mol is. Daarom gokken ze aan het einde van de aflevering maar wie ze denken dat de mol is. En om de kandidaten nog iets dommer te maken, lijden ze vanaf het begin aan extreme 'tunnelvisie': ze zetten altijd alle vragen in de test aan het einde van de aflevering op hun kandidaat-mol in, en spreiden hun kansen dus niet over meerdere personen. Ze blijven deze persoon verdenken totdat hij of zij uit het spel gaat. In dat geval kiezen ze in de volgende aflevering gewoon een willekeurige andere mol. Met zulke kandidaten heeft de mol het maar makkelijk, zou je zeggen. Toch ontcijferen zelfs dergelijke kandidaten vaak de mol!

Wie zit al goed in aflevering twee?

In de eerste aflevering zijn er $9$ kandidatenen één mol. De kandidaten kiezen compleet willekeurig een mol uit alle $8$ andere kandidaten en de mol. Dus, met deze strategie selecteert een kandidaat de juiste mol met kans $1/9$. Gemiddeld vult dan dus maar $\color{green}{9 \cdot 1/9 = 1}$ kandidaat de juiste mol in bij de test. Dit betekent dat er gemiddeld $8$ kandidaten de foute mol selecteren. Een van de kandidaten die het fout heeft, gaat uit het spel. We noemen deze kandidaat $k_1$. Iedereen die op kandidaat $k_1$ zat, kiest in de volgende aflevering een nieuwe mol.

Dit betekent dat er in de test van de tweede aflevering gemiddeld al meer mensen de juiste mol verdenken. De gemiddeld ene persoon die al vanaf aflevering één correct zat, blijft dat zo houden. Maar nu krijgen de personen die op kandidaat $k_1$ zaten ook een nieuwe kans om de juiste mol te identificeren. Hoe veel zijn dit er gemiddeld? De personen die fout zaten, zaten allemaal niet op de mol (en we gaan er ook vanuit dat ze niet zo dom waren dat ze zichzelf verdachten). Dit laat $8$ personen over, waarvan kandidaat $k_1$ die uit het spel ging er één is. Kortom, alle personen die het fout hadden, zaten met kans $1/8$ op kandidaat $k_1$. In aflevering twee zijn er nog $8$ andere personen over, dus selecteren ze in aflevering twee de juiste mol met kans $1/8$. Een kandidaat die het fout had in aflevering één, zit dus goed in aflevering twee met kans $\color{orange}{1/8 \cdot 1/8}$. Gemiddeld waren er $8$ kandidaten die het fout hadden in aflevering één. Eén van deze kandidaten valt af, dus in aflevering twee zijn er gemiddeld nog $\color{blue}{7}$ kandidaten die nog niet wisten wie de mol was in aflevering één. In totaal is het gemiddelde aantal kandidaten met het juiste antwoord in aflevering twee dus $1 + \color{blue}{7} \cdot \color{orange}{1/8 \cdot 1/8} \approx 1{,}11$ Dus in aflevering twee zijn er gemiddeld al meer kandidaten met het juiste antwoord dan in aflevering één, zelfs met zulke domme kandidaten.

Op naar aflevering drie

Stel dat in aflevering twee $c_2$ kandidaten de correcte mol ingevuld hadden. Dan blijven deze kandidaten in aflevering drie overtuigd van hun gelijk, en vullen dan ook weer de juiste mol in. Er zijn in totaal nog $7$ kandidaten in aflevering drie, dus zijn er gemiddeld $7 - c_2$ kandidaten die het fout hadden in de vorige aflevering. Met kans $1/7$ hadden deze kandidaten op de persoon die net uit het spel is gegaan gegokt, en moeten ze dus een nieuwe mol selecteren. Met kans $1/7$ is dit de correcte mol. Vergelijkbaar met aflevering twee, hebben dan gemiddeld

$$c_2+\frac{7-c_2}{7^2}$$

kandidaten de juiste mol ingevuld bij de test in aflevering drie. We hadden berekend dat gemiddeld genomen $c_2 = 1{,}11$, dus gemiddeld kiezen dan $1{,}11 + (7 - 1{,}11)/72 \approx 1{,}23$ mensen de juiste mol, alweer meer dan in aflevering twee.

Deze formule klopt alleen niet helemaal. Want wat als iedereen al de juiste mol had ingevuld in aflevering twee? In dat geval, als $c_2 = 8$, dan was er in aflevering twee iemand uit het spel gegaan die wel de juiste mol had ingevuld, en klopt de bovenstaande formule niet. Als je dit meeneemt krijg je dat het aantal kandidaten dat het in aflevering drie goed heeft gelijk is aan

$$\min\left(c_2+\frac{7-c_2}{7^2},7\right)$$

$(1)$

omdat er nooit meer dan $7$ kandidaten zijn in aflevering drie, ook niet als alle $8$ kandidaten uit aflevering 2 het goed hadden.

Versterkend effect

Met vergelijkbare formules als vergelijking $(1)$ kun je blijven doorrekenen hoeveel kandidaten gemiddeld op de juiste mol zitten. Dan kom je op deze grafiek uit.

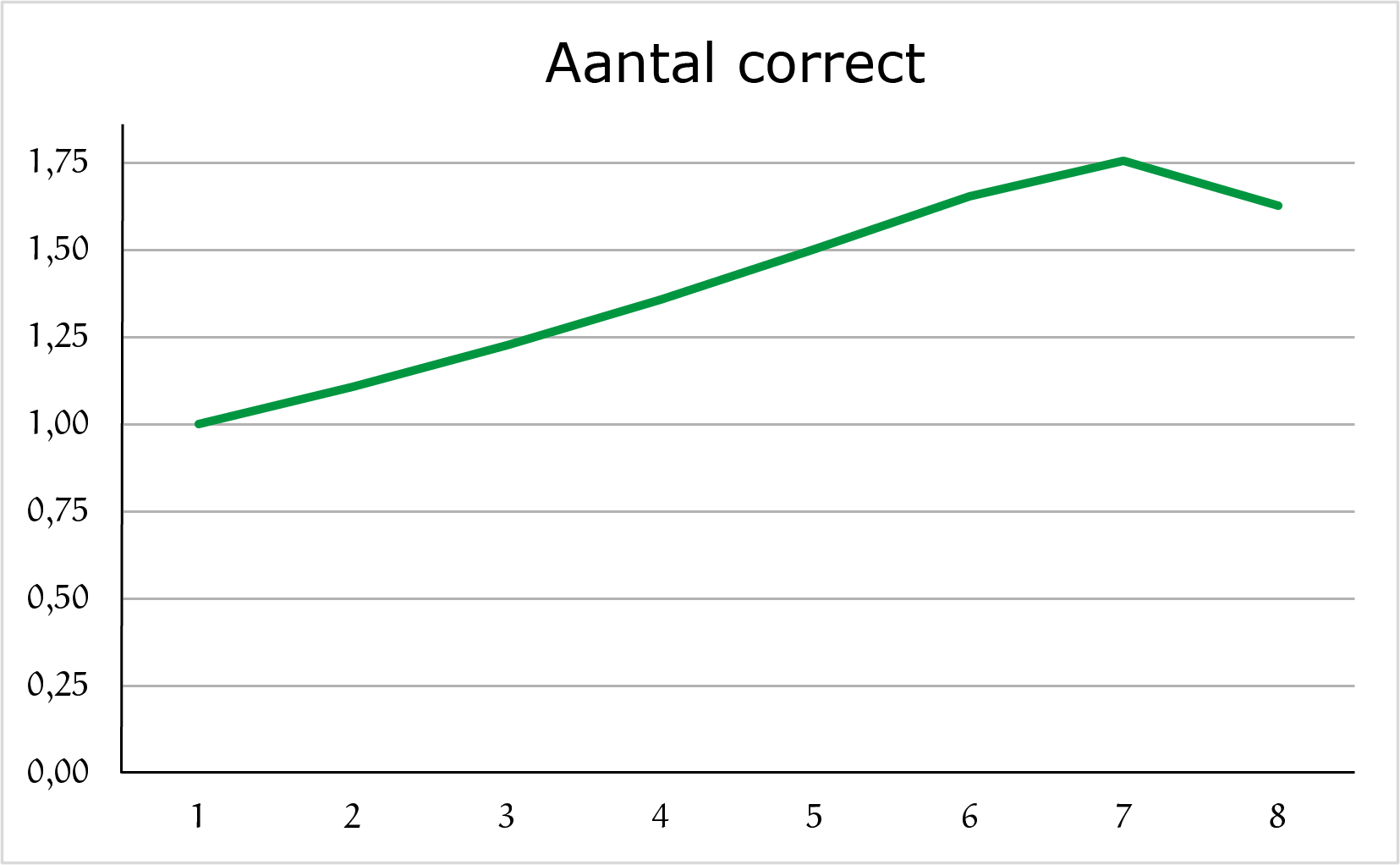
We zien dat in de finale gemiddeld wel $1{,}6$ van de overgebleven twee kandidaten op de juiste mol zitten! Iedere keer hebben de kandidaten die gokten op degene die uit het spel ging een nieuwe kans om de mol toch te vinden. We zien dus dat per aflevering het gemiddeld aantal kandidaten dat de juiste mol selecteert stijgt, behalve in de finale. Dit komt doordat in de halve finale vaak iedereen al de juiste mol raadt, waardoor er iemand uit het spel gaat die de juiste mol had. Dit is ook precies waarom het minimum in vergelijking $(1)$ nodig is.

Dit kunnen we ook zien in de volgende plot: wat is de kans dat alle domme kandidaten de juiste mol raden in de test? De eerste paar afleveringen is deze kans ongelofelijk klein. Maar in de finale is de kans dat iedereen de juiste mol heeft ongeveer $70%$!

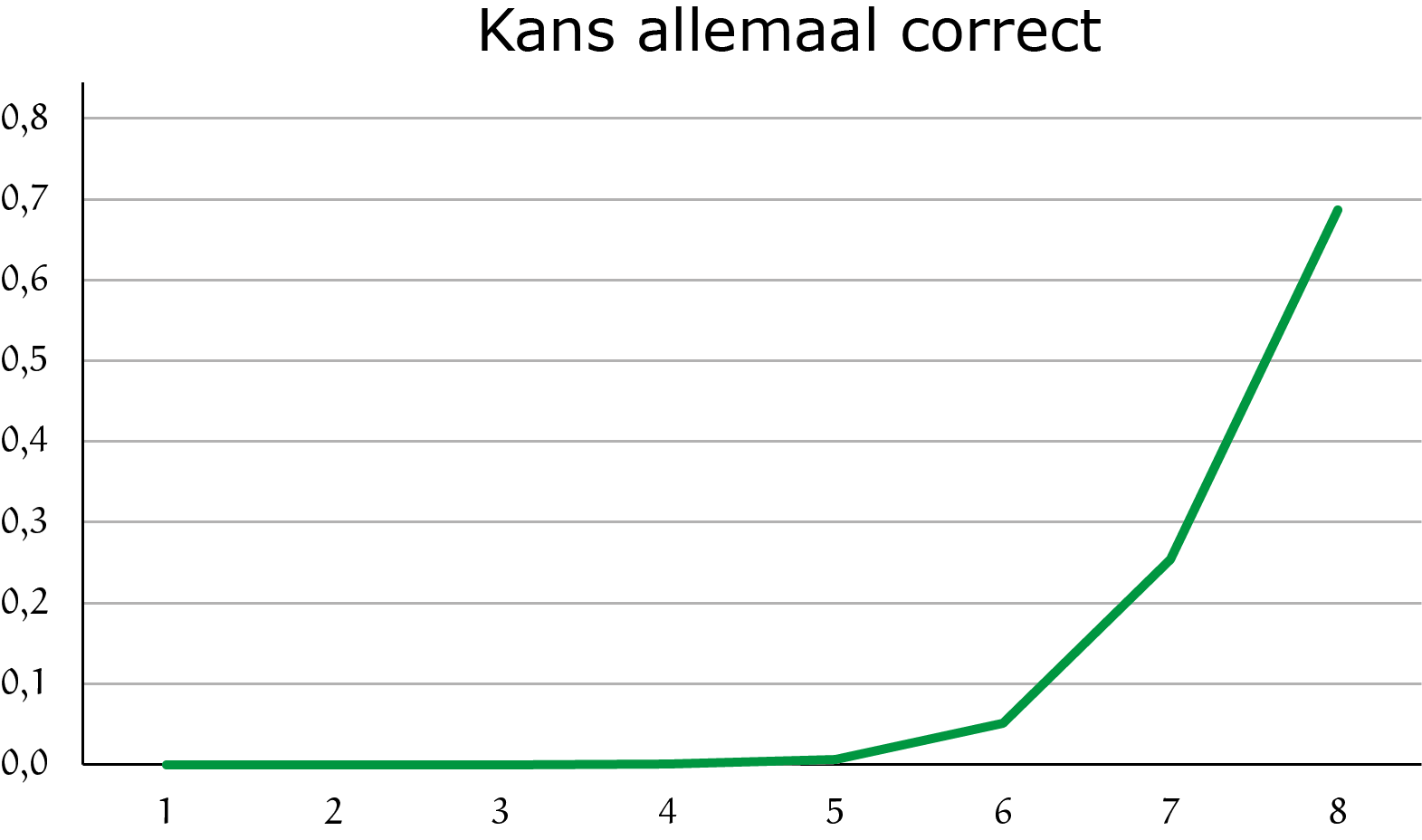
Kortom, als aan het einde van het spel iedereen weet wie de mol is, hoeft dit helemaal niet te betekenen dat de mol zo slecht is. Het kan ook gewoon wiskunde zijn.