De vlijtige leerling die bij de tweede ronde netjes van het begin naar het einde werkt, heeft al aardig wat hindernissen overwonnen om het tot vraag B4 te schoppen. Allereerst heeft deze leerling gevochten met de vraag wanneer de sommen van de cijfers van twee opeenvolgende getallen beide deelbaar zijn door $5$, om vervolgens de oppervlakte uit te rekenen van een parallellogram, waar op het eerste gezicht niet genoeg informatie voor gegeven lijkt te zijn. De derde opgave was opnieuw van een compleet verschillende aard; hier werd gevraagd om te bepalen wat er met de vakjes van een $8\times8$-vierkant gebeurt als je dit vierkant herhaaldelijk doormidden vouwt - ook dit is geen eenvoudige klus. Vervolgens komt deze leerling dan aan bij de vraag B4, een vraag die geen enkel kenmerk overeen heeft met de inmiddels getrotseerde problemen. Deze vraag staat in het kader.

De opgave Honderd kabouters (vrouwelijke scouts) zitten in een grote kring om het kampvuur. Elke kabouter heeft één of meer kastanjes en geen twee kabouters hebben hetzelfde aantal kastanjes. Elke kabouter deelt haar aantal door het aantal van haar rechter buurvrouw en schrijft de rest op een groen briefje. Elke kabouter deelt haar aantal ook door het aantal van haar linker buurvrouw en schrijft die rest op een rood briefje. Als bijvoorbeeld Anja $23$ kastanjes heeft en haar rechter buurvrouw Bregje heeft er $5$, dan schrijft Anja dus $3$ op haar groene briefje en schrijft Bregje $5$ op haar rode briefje. Als het aantal verschillende resten op de honderd groene briefjes gelijk is aan $2$, wat is dan het kleinst mogelijke aantal verschillende resten op de honderd rode briefjes?

Zoals vaker het geval bij Olympiadesommen, lijkt er niet direct een voor de hand liggende strategie te zijn die hier zal gaan werken om het antwoord te bepalen. Daar komt nog bij dat het helemaal niet duidelijk is wat het antwoord zou moeten zijn. Zeker ligt het ergens tussen de $1$ en de $100$, maar aan welk uiteinde van dit spectrum aan mogelijkheden moeten we zoeken? Als er slechts $2$ antwoorden op de groene briefjes voorkomen, dan zou je misschien denken dat dat op de rode briefjes ook zou moeten lukken. Echter, misschien maakt het lage aantal op de groene briefjes het juist wel moeilijk om weinig getallen op de rode briefjes te krijgen; op dit moment is het nog moeilijk te zeggen. Een gulden regel bij de Olympiade is altijd: als je geen idee hebt hoe je het moet aanpakken, probeer gewoon wat uit. Wellicht verwerven we op deze manier wat inzicht.

Laten we kijken of we überhaupt een situatie kunnen bedenken die voldoet aan de eisen van de opgave. Wat voor mogelijke aantallen kastanjes zouden ertoe kunnen leiden dat er slechts twee groene getallen op de briefjes staan? Vaak loont het om de situatie zo simpel mogelijk te houden en het verzinnen van honderd verschillende aantallen kastanjes klinkt nogal moeilijk. Laten we dus de vraag versimpelen, en doen alsof er geen honderd kabouters zijn, maar veel minder, zeg zes.

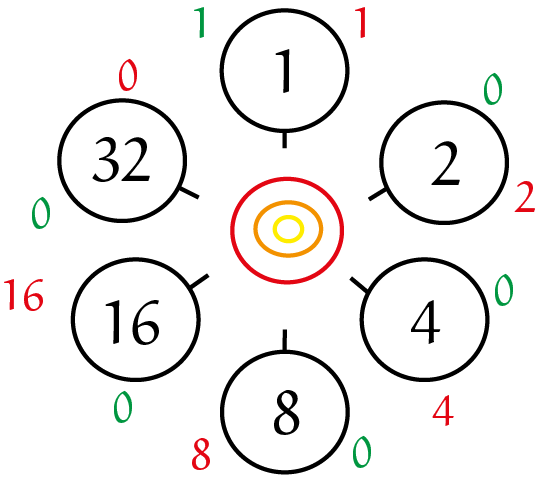Om het zo eenvoudig mogelijk te houden, laten we ook zeggen dat een van de kabouters, zeg kabouter 1, precies $1$ kastanje heeft. Haar linkerbuurvrouw, kabouter 2, zal haar aantal kastanjes delen door dat van kabouter $1$. Maar delen door $1$ levert nooit een rest, en dus zal kabouter 2 zeker het getal $0$ schrijven op haar groene briefje. Alle kabouters hebben een verschillend aantal kastanjes, dus in het eenvoudigste geval heeft kabouter 2 precies $2$ kastanjes. Laten we vanaf nu proberen altijd het getal $0$ op de groene briefjes te krijgen. Dit betekent dat het aantal kastanjes van elke kabouter een veelvoud moet zijn van dat van haar rechterbuur. We kiezen bijvoorbeeld dat kabouter 3 precies $4$ kastanjes heeft, en dat kabouter 4 bijvoorbeeld $8$ kastanjes heeft. Als we zo doorgaan, vinden we dat als kabouter 5 precies $16$ kastanjes heeft en kabouter 6 precies $32$ kastanjes heeft, bijna alle kabouters het getal $0$ op hun groene briefje hebben. Alleen kabouter 1 doet iets anders; als ze haar ene kastanje door de $32$ kastanjes van kabouter 6 deelt, houdt ze natuurlijk gewoon weer $1$ als rest over. In dit geval komen er dus in totaal twee verschillende getallen voor op de groene briefjes, namelijk $0$ en $1$. Dit is dus een situatie die voldoet aan het verhaaltje in de opgave, ware het dan met zes kabouters, in plaats van honderd.

Maar hoe zit het nu met de getallen op de rode briefjes? Kabouter 1 deelt haar aantal kastanjes door dat van kabouter 2. Maar 1 delen door $2$ geeft gewoon rest 1. Net zo deelt kabouter 2 het getal $2$ door $4$, maar dit geeft ook gewoon rest $2$. Net zo schrijven kabouters 3, 4 en 5 precies hun eigen aantal kastanjes op. Alleen bij kabouter 6 gebeurt er iets anders, want zij deelt haar aantal van $32$ kastanjes door $1$, en dit geeft natuurlijk rest $0$. Uiteindelijk vinden we dus dat alle resten op de rode briefjes in dit geval verschillend waren; dit geeft $6$ resten totaal.

Het bovenstaande zou kunnen worden opgevat als een mislukte poging. Ons wordt gevraagd om de laagst mogelijke waarde te vinden van het aantal verschillende getallen op de rode briefjes, en bovenstaand voorbeeld toont enkel aan dat het slechtst mogelijke geval, namelijk zes verschillende resten met zes kabouters, mogelijk is. Het lijkt alsof we nu helemaal niets zijn opgeschoten, maar niets is minder waar.

Wat we merkten bij het beschouwen van de rode briefjes is cruciaal. Als we een klein getal nemen en het delen door een groter getal, dan is de rest simpelweg gelijk aan het kleine getal. Dus stel dat een kabouter $a$ kastanjes heeft en de kabouter daar rechts van heeft er $b$, waar $a < b$, dan is de rest van $a$ bij deling door $b$ simpelweg gelijk aan $a$, en zo weten we zeker dat het getal $a$ op een groen briefje terecht komt. Er mogen echter maar twee verschillende getallen op de groene briefjes terecht komen, en dus kan deze situatie zich slechts hooguit twee keer voordoen. Dus de rechterbuurvrouw van een kabouter heeft altijd minder kastanjes dan zijzelf, op maximaal twee kabouters na. Dit is al enorm veel informatie!

We zijn er echter nog niet volledig. In ons voorbeeld was het zo dat de rechterbuur altijd minder kastanjes had, op slechts één kabouter na. Het zou echter nog kunnen dat er twee kabouters bestaan met, zeg, $a$ en $b$ kastanjes waar $a < b$, zodat voor alle kabouters behalve deze twee, de rechterbuur altijd minder kastanjes heeft. De twee resten die voorkomen op de groene briefjes moeten dus wel $a$ en $b$ zijn. Beschouw nu echter de kabouter links van de kabouter met $a$ kastanjes. Het getal op haar groene briefje wordt berekend door haar aantal kastanjes te delen door $a$ en dan de rest op te schrijven. Deze rest is altijd kleiner dan $a$, maar dat is gek! Namelijk, $a$ en $b$ waren de enige getallen die voorkwamen op de groene briefjes, dus er is niet ook nog ruimte voor een getal nog kleiner dan $a$. Dit kan dus niet gebeuren en we concluderen dat de enige mogelijkheid is dat de rechterbuur van elke kabouter minder kastanjes heeft, op slechts één kabouter na.

Maar nu zijn we er eigenlijk. Namelijk, we bevinden ons weer precies in de situatie van ons voorbeeld. Elke kabouter behalve de rechterbuur van de kabouter met het kleinste aantal kastanjes zal haar eigen aantal op het rode briefje schrijven. De laatste kabouter schrijft een getal op dat kleiner is dan al die getallen, omdat zij de rest opschrijft bij deling door het kleinste voorkomende aantal kastanjes, en dat is altijd nòg kleiner. Dit zijn dus altijd $100$ verschillende getallen en daarom moeten er op de rode briefjes altijd $100$ verschillende getallen voorkomen.

Het bovenstaande is een voorbeeld van een opgave die erg moeilijk op te lossen is, tot je het probleem versimpelt en probeert om een situatie te vinden waar de opgave over spreekt. Dan is het direct veel minder abstract, en blijkt veel van de vrijheid die je op het eerste gezicht lijkt te hebben, direct te verdwijnen als sneeuw voor de zon. De structuur van de situatie wordt dan veel duidelijker en dan is het nog slechts een bescheiden stap naar het juiste antwoord. Een echte doordenker, zoals het op de Olympiade ook hoort.