Kleine nootjes zijn eenvoudige opgaven die weinig of geen wiskundige voorkennis vereisen om opgelost te worden. De antwoorden vind je onderaan zodra het volgende nummer van Pythagoras verschenen is.

Deze jaargang is er steeds een speciaal nootje over poolbiljart.

12=34?

In het 5-tallig stelsel is het getal $(42)_5 = 4 \times 5 + 2 = (22)_{10}$ in het tientallig stelsel.

Wat zijn de kleinste getallen $m$ en $n$, zodat: $(12)_m = (34)_n$?

Het was een hete zomer

Bekijk de volgende optelling. 

      H  E  T
      W  A  S
         Z  O
   ------------ +
   W  A  R  M

Er komen 10 verschillende letters in voor. Gebruik alle cijfers van 0 tot en met 9. Gelijke letters zijn gelijke cijfers. Zoek een oplossing van deze optelling.

BMI

De Body-Mass-Index of $\rm BMI$ is gedefinieerd als: ${\rm BMI} = G/L^2$.

Hierin is $L$ de lengte van de persoon in meters en $G$ het gewicht in kilogrammen.

Het aanbevolen gebied voor een gezond gewicht is een $\rm BMI$ tussen $20$ en $25$. Obesitas begint bij ${\rm BMI} = 30$.

Kees zegt: ‘Mijn moeder zei vroeger: als je net zoveel kilogrammen weegt als je centimeters boven de meter meet, heb je een goed gewicht. En daar zit ik precies op. Maar mijn $\rm BMI$ is maar net in orde.’

Hoeveel weegt Kees en hoe lang is hij?

Buiten, binnen, evenwijdig?

In een regelmatige zevenhoek worden at random 2 diagonalen getekend. Bepaal de kans dat dit paar zijn snijpunt op, binnen of buiten de zevenhoek heeft of dat het evenwijdig is. (Met dank aan Kees Vugs.)

Poolbiljart

Kan je met de ballen 1 t/m 6 onderstaande driehoeken afmaken zodat geldt: het getal op elke bal is het verschil van de twee ballen die erboven liggen?

 

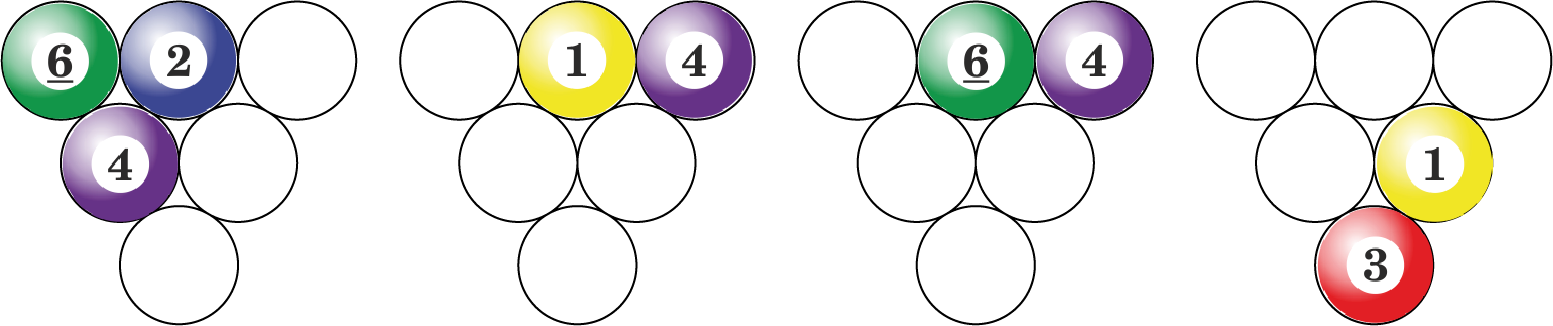
Bekijk oplossing