POOLBILJART

$6$  $2$  $5$    $6$  $1$  $4$    $1$ $6$  $4$    $2$  $6$  $5$
  $4$  $3$        $5$  $3$         $5$  $2$        $4$  $1$
    $1$            $2$              $3$             $3$

HET WAS EEN HETE ZOMER

    $9$  $2$  $8$
    $1$  $0$  $4$
         $3$  $5$
----------- +
$1$  $0$  $6$  $7$

12=34?

Er geldt: $(12)_{17} = (34)_5$. Dus $m = 17$ en $n = 5$. Je krijgt dan het getal $19$ in het tientallig stelsel.

BMI

Kees’ moeder zei: ‘$G = (L – 1) × 100$’. Een net niet te hoog BMI is $25$. Dan geldt: $G/L^2 = (L – 1) × 100/L^2 = 25$. Dus: $L^2 – 4L + 4 = 0$. Of: $(L – 2)^2 = 0$. En dus: $L = 2$ meter en $G = (L – 1) × 100 = 100$ kilogram.

BUITEN, BINNEN, EVENWIJDIG?

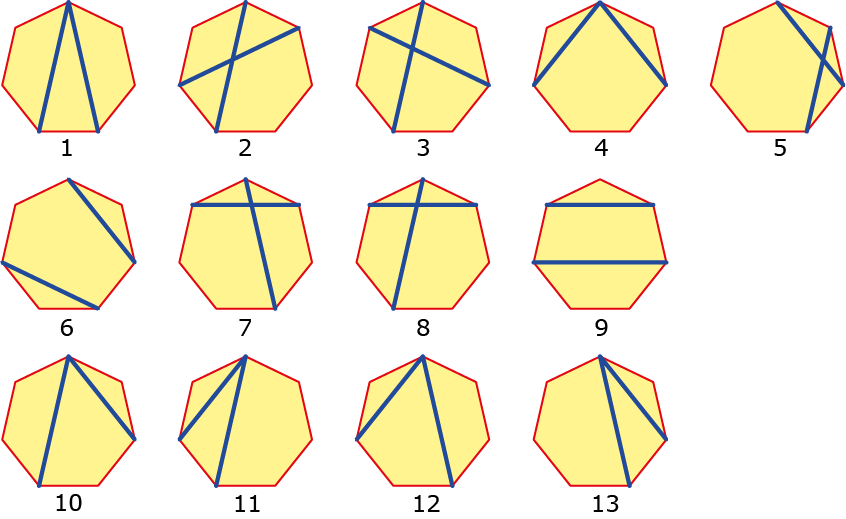Een regelmatige zevenhoek heeft $7$ lange diagonalen en $7$ korte, waaruit $14x13\div 2=91$ paren gekozen kunnen worden.

• Kies je $2$ lange dan hebben $7$ paren hun snijpunt op de zevenhoek (figuur $1$), $14$ paren hun snijpunt binnen de zevenhoek (figuren $2$ en $3$) en geen paar buiten de zevenhoek of evenwijdig.
• Kies je $2$ korte dan hebben weer $7$ paren hun snijpunt op de zevenhoek (figuur $4$), $7$ paren binnen de zevenhoek (figuur $5$) en $7$ paren buiten de zevenhoek (figuur $6$) en zijn er geen evenwijdige paren.
• Kies je $1$ lange en $1$ korte diagonaal, dan hebben $14$ paren hun snijpunt binnen de zevenhoek (figuren $7$ en $8$), $7$ evenwijdige paren (figuur $9$) en $28$ paren op de zevenhoek (figuren $10$, $11$, $12$ en $13$) en geen buiten de zevenhoek.

Samenvattend: kans op $= 42/91 = 6/13$, kans binnen $= 35/91 = 5/13$, kans buiten $= 7/91 = 1/13$ en kans evenwijdig $= 7/91 = 1/13$. Samen natuurlijk $1$.