Veelhoeken

Je kunt in de figuur van $3 \times 3$ punten vierhoeken tekenen. (Zijden mogen elkaar niet snijden, behalve uiteraard in de hoekpunten van de veelhoek. Op een zijde mag nog een derde punt liggen, dat natuurlijk niet meetelt als hoekpunt. Congruentie mag er ook niet zijn na draaiing, verschuiving of spiegeling.)

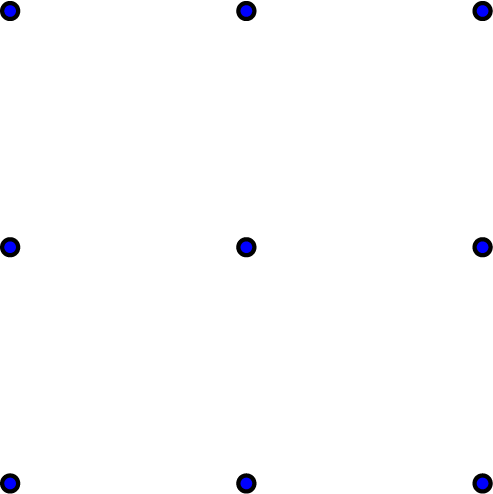
Hoeveel verschillende vierhoeken kun je maken zonder spiegel- of rotatiesymmetrie?

Niets over

Je hebt een stapel munten van $1$ euro. Vandaag geef je er een zeker percentage van uit. Morgen geef je $10%$ meer uit van de munten die je dan over hebt. Overmorgen geef je nog $10%$ meer uit. Dan heb je niets  meer over.

Hoeveel euromunten had je minimaal?

Spel met zes kaarten

Twee vrienden Kaj en Kjeld spelen steeds een spel met zes kaarten. Op elke zijde staat een cijfer. De kaarten hebben de volgende cijfers: $(1,1), (2,2), (3,3), (1,2), (1,3), (2,3).$  Kaj neemt blind een willekeurige kaart en legt hem met een willekeurige zijde naar boven op tafel. Wat boven is, is Kajs getal.

Nu is Kjeld aan de beurt. Hij mag de kaart laten liggen of hij mag die kaart omdraaien. De bovenkant is nu Kjelds getal. Als Kjeld ervoor kiest de kaart niet om te draaien, zijn de getallen van Kjeld en Kaj gelijk en gaan ze over naar het volgende spel. Bij ongelijke getallen wint degene met het grootste getal. Hij krijgt dan 1 euro van de ander. Kjeld kan ervoor kiezen nooit een kaart om te draaien. Dan verliest hij dus nooit, maar wint ook niets. Maar kan hij ook winnen? Hoe  moet Kjeld spelen om gemiddeld het meeste te verdienen?

Alle wegen lopen

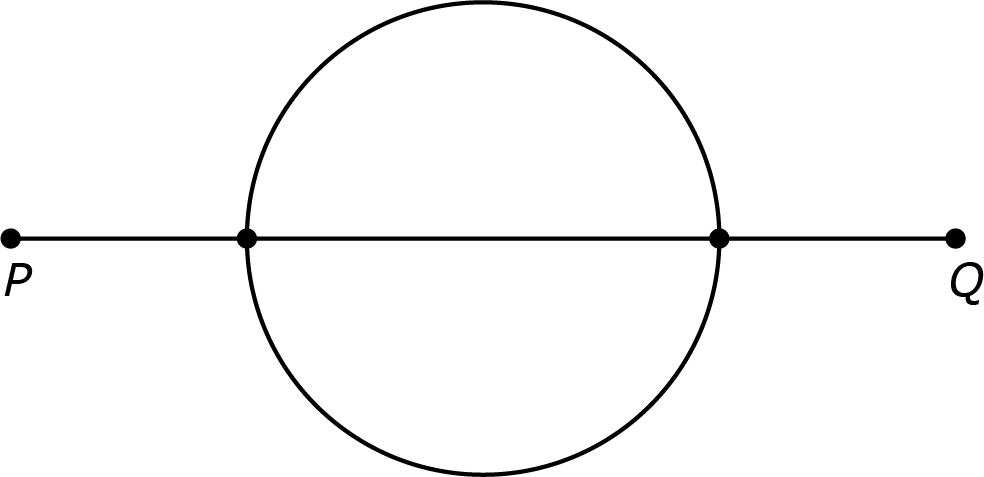
In de bovenste figuur zie je 5 weggedeeltes. Je loopt van $P$ naar $Q$ en wilt alle weggedeeltes precies één keer lopen. Kruispunten passeren mag meerdere keren.

Op hoeveel verschillende manieren kun je van $P$ naar $Q$ lopen?

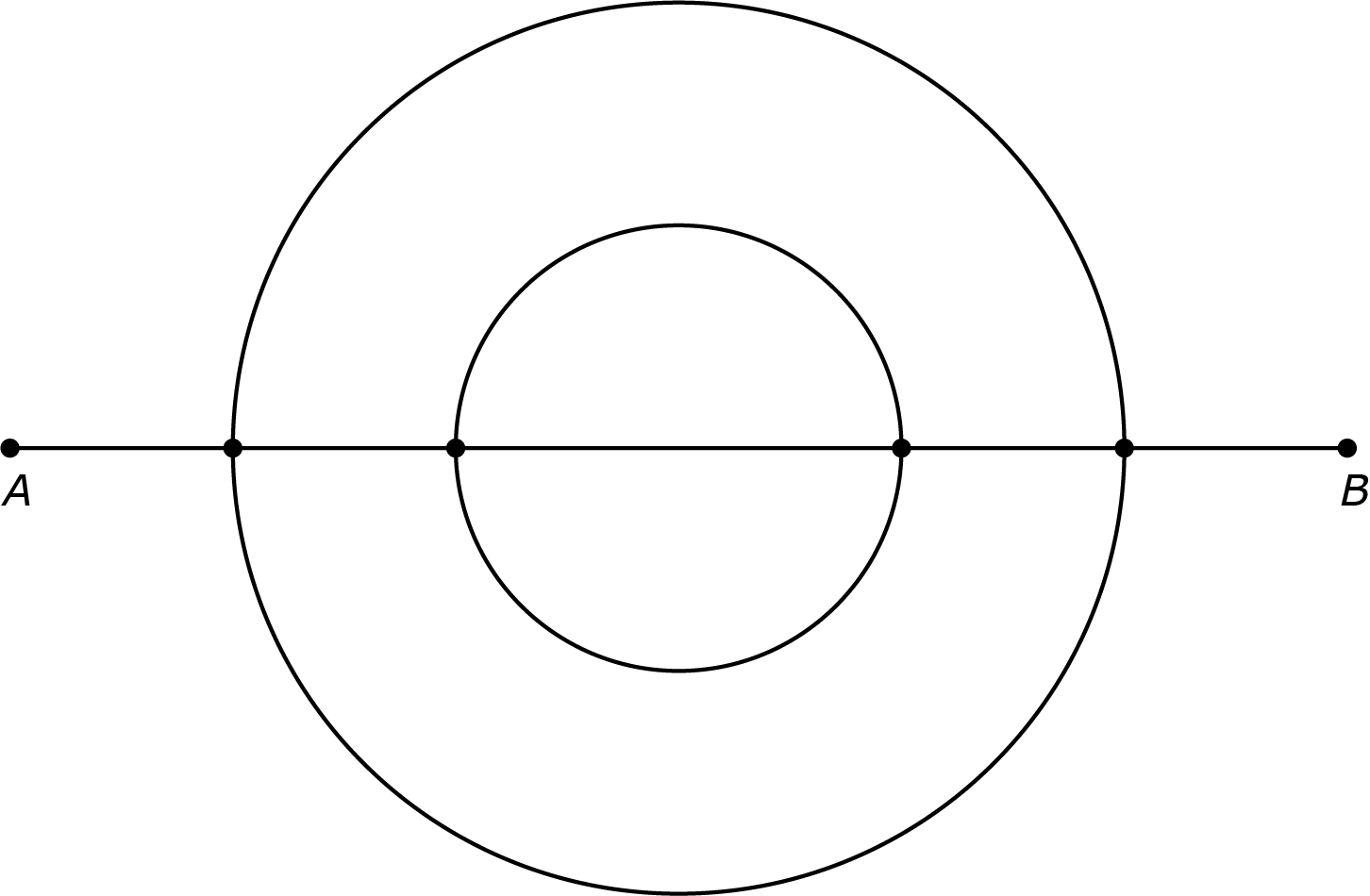
Kijk vervolgens naar de volgende figuur. Op hoeveel verschillende manieren kun je nu van $A$ naar $B$ lopen, waarbij je weer elk weggedeelte precies één keer passeert?

Bonbons

Madelon houdt erg van bonbons. Maar ze  wil er niet elke dag van eten, hoewel dat niet altijd lukt. Maandag eet ze twee bonbons meer dan woensdag. Haar gemiddelde over maandag en dinsdag is 50% meer dan dat over dinsdag en woensdag.

Haar gemiddelde over maandag, dinsdag en woensdag is gelijk aan het aantal dat ze eet op maandag.

Slaagt Madelon erin om op een van de dagen geen bonbons te eten?

Bekijk oplossing