AaNvuLling

In het vorige nummer verscheen de oplossing van het Nieuwjaarsprobleem GELUKKIG 2019. De oplossingen liepen tot 30. Aad van de Wetering gaf extra oplossingen tot en met 42. Daarvoor dank.

31=29 + 1 + 0!
32=10 × √9 + 2
33=√9 × (12 – 0!)
34=10 + ((√9)!-2)!
35=√9 × 12 – 0!
36=√9 × 12 + 0
37=√9 × 12 + 0!
38=2 × 19 + 0
39=√9 × (12 + 0!)
40=120 / √9
41=√(2¹⁰) + 9
42=21 × (√9 – 0!)

Zijn dit ze dan nu wel allemaal?

BONbonS

De aantallen die ze eet op maandag, dinsdag en woensdag, zijn $m, d$ en $w.$ Dan gelden: $m = w + 2, (m + d) : 2 = (3 : 2)(d + w) : 2, (m + d + w) : 3 = m.$

De oplossing is: $m = 2, d = 4, w = 0.$ Het is Madelon dus gelukt.

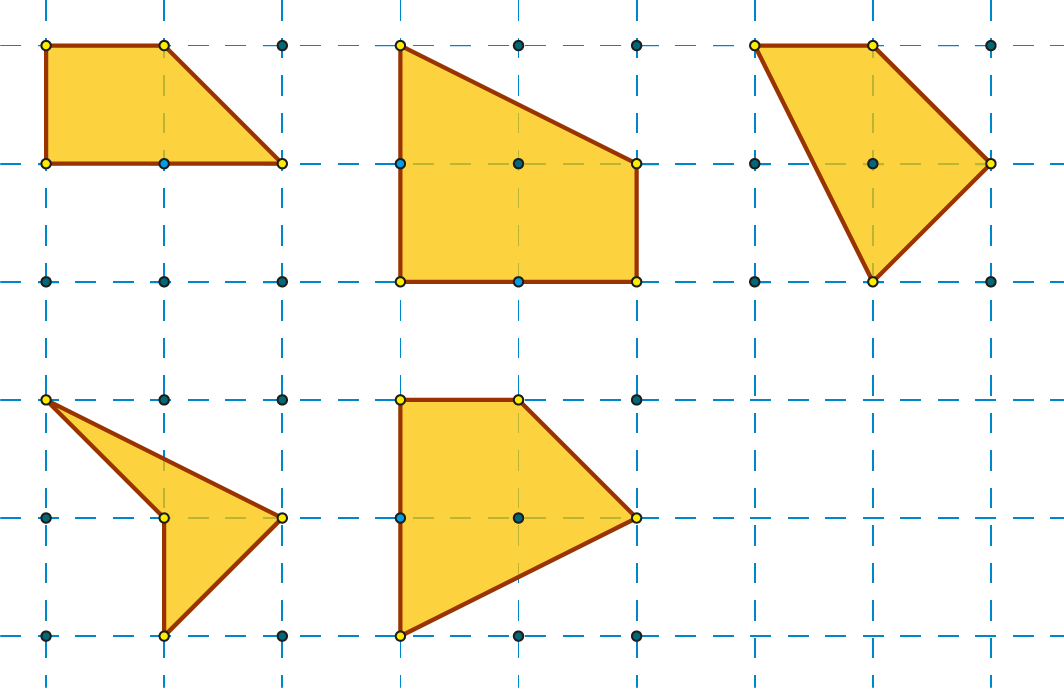
VEeLHOEKEN

Er  zijn vijf vierhoeken zonder symmetrie.

NIETS OVeR

Op de derde dag maak je alles op. Dus dan is je percentage $100.$ De dag daarvoor dus $90,$ en de eerste dag $80.$ Stel je begint met $E$ euromunten. Dan geef je op dag 1 $0{,}8 \cdot E$ munten uit en houdt er $0{,}2 \cdot E$ over. Op dag 2 geef je $0{,}9 \cdot 0{,}2 \cdot E$ munten uit en houd nog $0{,}02 \cdot E$ munten over. Op dag 3 geef je de rest uit. Die rest van $0{,}02 \cdot E$ moet minstens 1 euro zijn. Dus $E = 50$ euromunten.

SPEL MeT ZES  KaARtEN

In elke serie van 12 spellen komt elk van de 12 kanten gemiddeld 1 keer boven.

• Vier keer een 3. Dan doet Kjeld niets. Hij kan hoogstens verliezen.
• Vier keer een 2. Als Kjeld niets doet wint hij niets. (Als Kjeld ervoor kiest om de kaart  om te draaien, dan ziet hij 2 keer een 2, 1 keer een 1 (verlies) en 1 keer een 3 (winst). Dat levert dus niets op.)
• Vier keer een 1. Kjeld draait de kaart om. Dan ziet hij 2 keer een 1, en een 2 of een 3 (beide winst).

Kjeld wint dus in 2 van de 12 spelletjes. Of 1/6 euro per spel.

ALlE WeGEN LOPEN

Er zijn 6 verschillende routes van $P$ naar $Q.$ Als je van $A$ naar $B$ gaat, heb je weer 6 routes, waarbij het ‘binnenstuk’ voor 6 telt. Er zijn dus $6 \times 6 = 36$ verschillende wegen.