Veelhoeken

Je kunt in een vierkant van $3 \times 3$ punten vierhoeken tekenen met de hoekpunten op de $9 $ punten van de figuur. Zijden mogen elkaar niet snijden en op een zijde mag nog een derde punt liggen, dat natuurlijk niet meetelt als hoekpunt. Hoeveel verschillende vierhoeken kun je tekenen waar precies één van de $9$ punten strikt binnen ligt? Congruente vierhoeken die gedraaid, gespiegeld of verschoven zijn tellen niet extra.

Maxima

Zet de getallen $1$ tot en met $6$ bij de hoekpunten van een regelmatige zeshoek. Zet bij elke zijde het verschil (positief) van de getallen bij de twee eindpunten. Hoe moet je ze plaatsen om de som van de zes verschillen zo groot mogelijk te maken? Zet nu bij de zes zijden het product van de getallen bij de twee eindpunten. Hoe moet je ze nu plaatsen om de som van de zes producten zo groot mogelijk te maken?

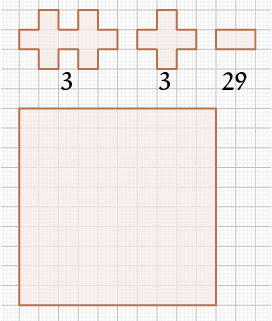Bord bedekken

Je hebt drie soorten puzzelstukken: $ 3$ grote van $9$ vierkantjes groot, $3$ kleinere van $5$ vierkantjes groot en $29$ kleine van elk $2$ vierkantjes groot. In totaal kun je hiermee een oppervlakte van $3\times 9 + 3\times 5 + 29\times 2=100$ vierkantjes bedekken. Kun je er een vierkant bord van $ 10\times 10$ mee bedekken?

Zoek de getallen

Zoek acht verschillende cijfers uit $0, 1, 2, 3, 4, 5, 6, 7, 8, 9$. Maak daarmee vier getallen van twee cijfers. Als je nu $1$ optelt bij elk van die vier getallen, krijg je soms opnieuw vier getallen van twee cijfers met acht verschillende cijfers. Een voorbeeld is: $20, 49, 63, 78$. Na optellen van $1$ krijg je $21, 50, 64, 79. $ Probeer hetzelfde, waarbij je $2$ bij elk getal van twee cijfers optelt. En ook voor $3, 4, 5, 6, 7, 8$ en $9$. Bij $9 $ is er een oplossing waarbij beide sets van vier getallen alleen de cijfers $1$ tot en met $8$ bevatten.

Minder prikkers

Schrijf met cocktailprikkers een ware berekening, met de cijfers in letters ($+$ met $2$ prikkers, $-$ met $1$, $/$ met $1$, $\times$ met $2$, $E$ met 4, $F$ met $3$, $R$ met $5$). Voorbeeld: $E\ E\ N + D\ R\ I\ E = V\ I\ E\ R$. Deze som kun je leggen met $41$ cocktailprikkers. Controle: $4+4+3+2+4+ 5+1+4+2+2+1+4+5=41. $ Wat is het kleinste aantal cocktailprikkers waarmee je een soortgelijke som kunt leggen?

Bekijk oplossing