VeElhoeken

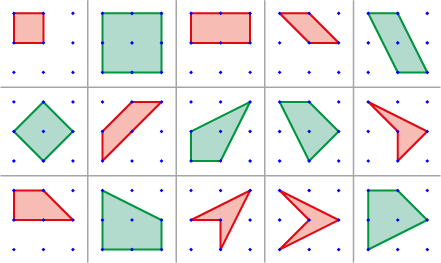
Er zijn $7$ oplossingen met een punt binnen de vierhoek.
Zie de figuur met alle mogelijke vierhoeken.

MaximA

Maximale som: $1\ 5\ 3\ 4\ 2\ 6$ (de $6$ staat naast de $1$). De maximale som is $4 + 2 + 1 + 2 + 4 + 5 = 18$. 

Maximaal product: $1\ 2\ 4\ 6\ 5\ 3$ (de $3$ staat naast de $1$). De maximale som hierbij is $2 + 8+ 24 + 30 + 15 + 3 = 82$.

Zoek de getalLen

Tel $2$ op bij $40, 51, 69, 87$ en krijg $42, 53, 71, 89$.
Tel $3$ op bij $40, 59, 72, 86$ en krijg $43, 62, 75, 89$.
Tel $4$ op bij $13, 56, 78, 90$ en krijg $17, 60, 82, 94$.
Tel $5$ op bij $12, 34, 57, 80$ en krijg $17, 39, 62, 85$.
Tel $6$ op bij $12, 34, 56, 87$ en krijg $18, 40, 62, 93$.
Tel $7$ op bij $12, 43, 57, 80$ en krijg $19, 50, 64, 87$.
Tel $8$ op bij $12, 43, 65, 78$ en krijg $20, 51, 73, 86$.
Tel $9$ op bij $12, 34, 56, 78$ en krijg $21, 43, 65, 87$.

Bord bedEkKen

Neem een dambord van $10 \times 10$ met afwisselend zwarte en witte velden. Er zijn evenveel zwarte als witte velden. De kleine puzzelstukken bedekken net zoveel zwarte als witte velden. Als je een groot puzzelstuk legt, bedek je $7$ zwarte en $2$ witte velden (of omgekeerd). Dan heb je, afhankelijk van de plaatsing, een overschot van $5$ of $15$ zwarte velden. Die moeten goed gemaakt worden met de drie puzzelstukken van $5$ vierkantjes. Zo’n stuk heeft een overschot van $3$ witte velden (of omgekeerd). Een overschot van $5$ zwarte velden kun je niet goedmaken, omdat $3$ geen deler is van $5$. En een overschot van $15$ zwarte velden kun je niet goedmaken, omdat je maar drie stukjes hebt met een overschot van $3$ witte velden. Je kunt met deze set puzzelstukken het bord dus niet bedekken.

Minder priKkeRs

$ELF - ELF = NUL$

kan met $4 + 2 + 3 + 1 + 4 + 2 + 3 + 2 + 3 + 3 + 2 = 29$ prikkers.