Kleine Nootjes 59-6
SymMetrische vergelIjkingen
- Kun je vier positieve gehele getallen $a, b, c$ en $d$ vinden die aan de volgende twee vergelijkingen voldoen: $ab = c + d$ en $cd = a + b$? Hoeveel oplossingen kun je vinden?
- Kun je oplossingen vinden met $a = 0$?
(Met dank aan Nico van Wageningen.)
TwEe keEr rond?
Op een hardloopbaan van 400 meter start een hardloopster. Ze loopt op een rare manier. Ze gooit bij de start een muntje op en loopt dan bij kop via de linkerhelft $L$ van de baan en bij munt via de rechterhelft $R$ van de baan, in beide gevallen 200 meter, tot precies de overkant. Daar aangekomen gooit ze weer het muntje op om terug te keren naar het beginpunt, bij kop weer via de linkerkant van de baan en bij munt weer via de rechterkant. Dit doet ze vijf keer. Het kan voorkomen dat ze de baan in twee halve banen achter elkaar keurig in het rond loopt (linksom of rechtsom). Dat kan zelfs daarna nog een keer gebeuren.

Hoe groot is de kans dat ze in die 1000 meter de baan twee keer volledig rond loopt, in twee halve rondes achter elkaar en beide rondes ook in dezelfde richting?
ÉéN van de gewichten is 1
Alle gewichtjes in dit vraagstuk zijn een geheel veelvoud van $1$ gram. Je neemt een enkel gewichtje. Als je er twee gelijke gewichtjes aan toevoegt, daalt het gemiddelde van de drie gewichtjes naar $10$ onder het eerste gewichtje. Als je er
dan drie gelijke gewichtjes aan toevoegt, daalt het gemiddelde weer met $10$. Ten slotte voeg je er vier gelijke gewichtjes aan toe, waardoor het gemiddelde weer gelijk aan het eerste gewichtje is. Kan één van de gewichtjes $1$ gram zijn?
Welk gewichtje is dat dan en hoe zwaar zijn de andere gewichtjes?
Hoe grOot is het vierkant?
In het vierkant in de figuur zijn twee gekleurde oppervlaktes, $A$ en $B$, gegeven.
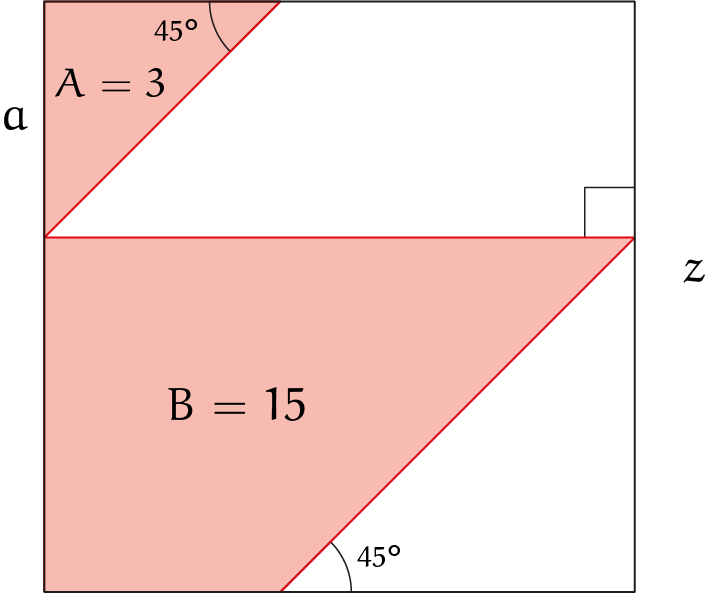
Hoe groot zijn de zijden $z$ van het vierkant?
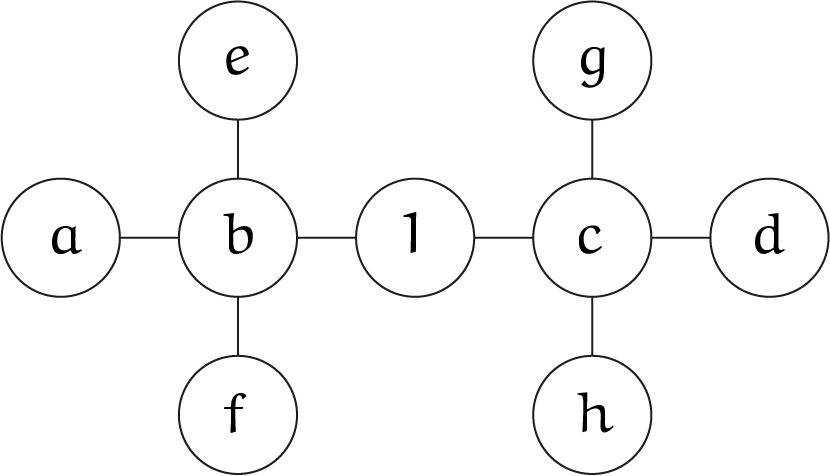
éÉn in het miDden
In de negen cirkels in de figuur moeten de getallen $1$ tot en met $9$ geplaatst worden. Het cijfer $1$ staat in het midden. Er zijn vier drietallen die allemaal dezelfde som hebben: $a + b + 1 = 1 + c + d = e + b + f = g + c + h$.
Vind de getallen $a$ tot en met $h$.