DobBelstEen

Je kijkt met één oog naar een dobbelsteen. Dan kun je één zijvlak zien, of twee of drie, meer niet. Je kunt bijvoorbeeld de dobbelsteen zo houden, dat je de $1$, de $3$ en de $5$ ziet, samen $9$. Mijn bewering is: je kunt de dobbelsteen zo voor je oog draaien dat je alle sommen $1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14$ en $15$ kunt zien. 

Is mijn bewering juist?

KubUspuZzel

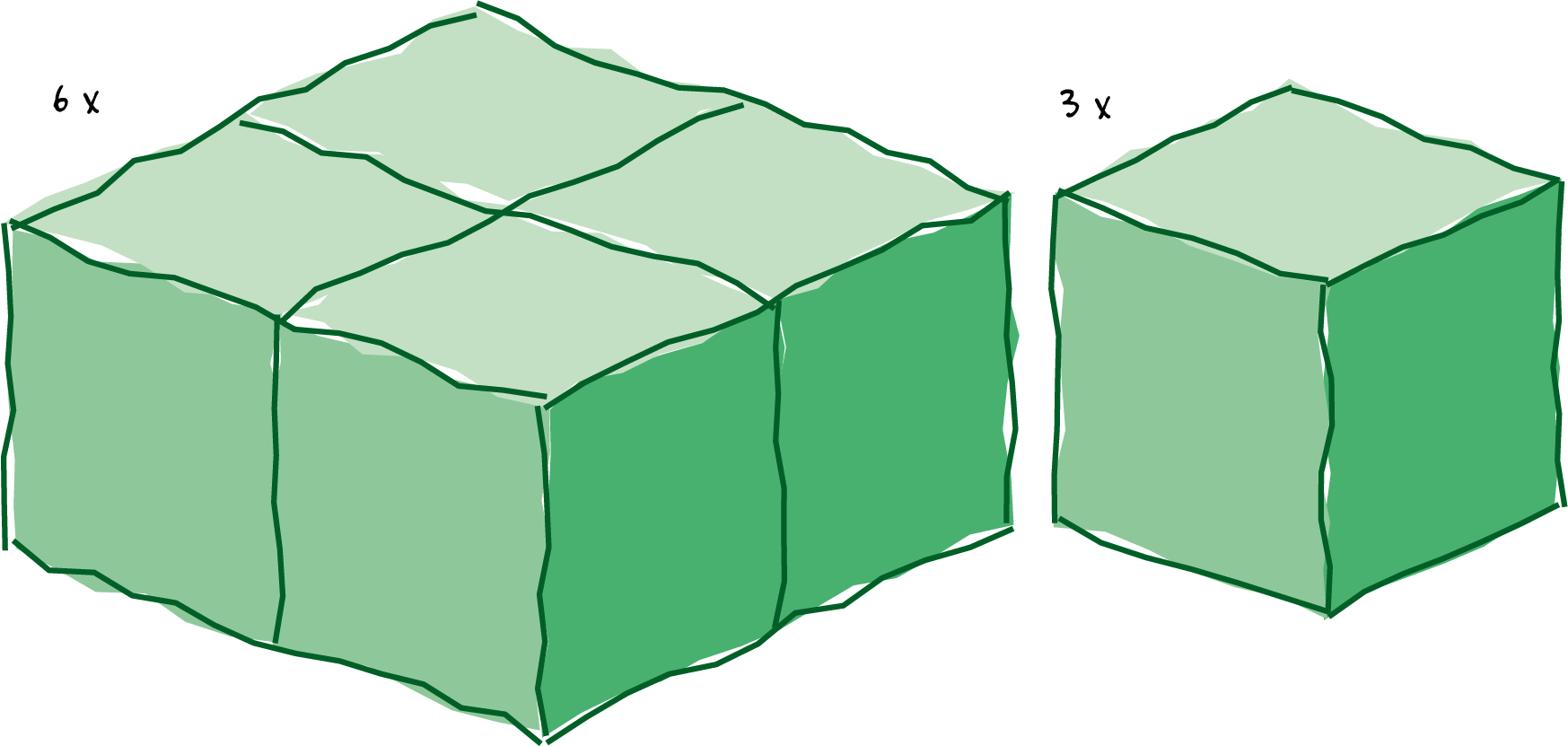
Neem $27$ identieke kleine kubusjes. Daarmee kun je natuurlijk een grote kubus van $3 \times 3 \times 3$ opstapelen. Je kunt ook $4$ van de kubusjes in een vierkant aan elkaar plakken $(2 \times 2 \times 1)$. Als je dat zes keer doet, heb je in totaal $9$ puzzelstukken ($6$ grote van $4$ en $3$ kleine van $1$).

Kun je met deze $9$ stukken weer een kubus van $3 \times 3 \times 3$ maken?

AutobioGrafisCh getal

$2020$ is een zogenaamd autobiografisch getal, want het bevat in volgorde $2$ keer een $0$, $0$ keer een $1$, $2$ keer een $2$ en $0$ keer een $3$. Ook $1210$ is een autobiografisch getal. In een autobiografisch getal $abcdefg$ van $7$ cijfers staat dus $a$ keer een $0$, $b$ keer een $1$, $c$ keer een $2$ tot en met $f$ keer een $5$ en $g$ keer een $6$.

Bepaal dat getal.

Honingbij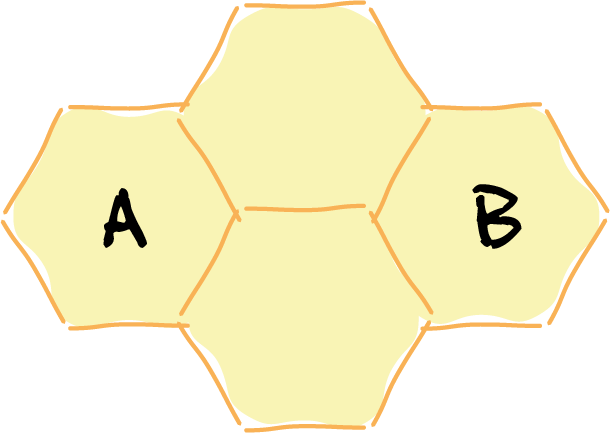

Een bij vliegt van cel naar cel. Daarbij gaat ze telkens van een cel naar een willekeurige aangrenzende cel, elk met gelijke kans. Zo kan ze in twee keer vliegen van cel $A$ naar cel $B$ komen, maar meestal doet ze daar langer over. Hoeveel vluchten 
heeft ze gemiddeld nodig om van $A$ naar $B$ te komen?

Waarheid en leugen

Om een grote ronde tafel zitten $13$ mensen. Een deel liegt altijd en het andere deel spreekt altijd de waarheid. Iedereen weet wie van de anderen de waarheid spreekt of liegt. Ze kijken allemaal naar hun twee buren links en twee buren rechts. Ze zeggen dan allemaal: 

"Bij mijn vier buren, twee links en twee rechts, zitten minstens twee leugenaars."

1. Bedenk een volgorde waarin deze $13$ mensen rond de tafel kunnen zitten.
2. Bedenk ook een volgorde als er maar $11$ mensen rond de tafel zitten.
3. Bestaat er een volgorde voor alle aantallen groter dan $4$?

Bekijk oplossing