AutObiografisch getal

Het gezochte getal is $3211000$. Immers het bevat $3$ keer een $0$, $2$ keer een $1$, $1$ keer een $2$, $1$ keer een $3$, $0$ keer een $4$, $0$ keer een $5$ en $0$ keer een $6$.

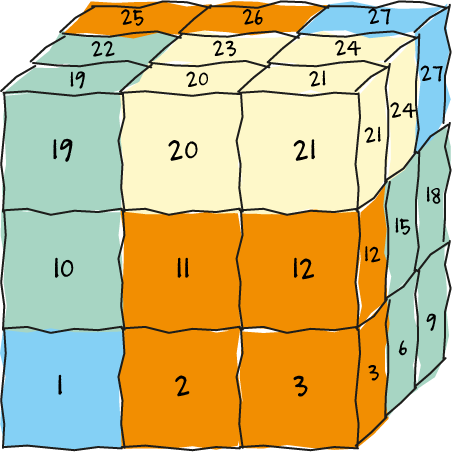
KubUspuZzel

Een oplossing is de volgende. Nummer de $27$ plaatsen in de $3\times 3\times 3$-kubus in het ondervlak van links naar rechts en van voren naar achter met $1, 2, 3; 4, 5, 6; 7, 8, 9$. In het horizontale middenvlak krijgen we dan $10, 11, 12; 13, 14, 15; 16, 17, 18$. En in het bovenvlak $19, 20, 21; 22, 23, 24; 25, 26, 27$. Zet in het voor- en achtervlak twee grote stukken zo, dat het hoekblokje rechts-voor-onder bedekt is door het voorste stuk en het hoekblokje links-achter-boven bedekt is door het achterste stuk. De twee stukken bedekken dan de nummers $(2, 3, 11, 12)$ en $(16, 17, 25, 26)$. Zet dan in het boven- en ondervlak weer twee grote stukken met de nummers $(20, 21, 23, 24)$ en $(4, 5, 7, 8)$. Zet ook in het linker- en rechterzijvlak twee grote stukken op de nummers $(6, 9, 15, 18)$ en $(10, 13, 19, 22)$. Zet de drie enkele stukjes op de nummers $1$, $14$ en $27$ op een lichaamsdiagonaal.

DobBelsteEn

Je zult met enig proberen uitvinden dat je alle sommen op de dobbelsteen kunt zien, behalve $13$. Dat kan niet, omdat je in ieder geval de $6$ moet zien. Met $5$, $4$ en $3$ kom je niet verder dan $12$. Dan moet je met de andere twee kanten nog $13 - 6 = 7$ samen zien. Dan zou je $2$ en $5$, of $3$ en $4$ nodig hebben. Maar die zitten tegenover elkaar. Dus $13$ gaat niet lukken.

HoNingbIJ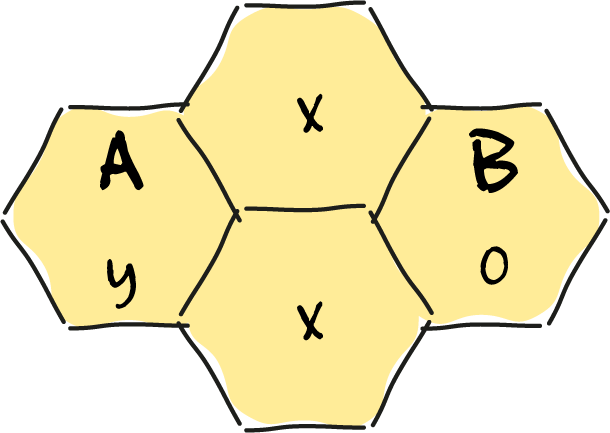

Noem het gemiddeld aantal vluchten dat de bij nodig heeft om van $A$ naar $B$ te komen $y$, en het aantal om van een van de middelste cellen naar $B$ te komen $x$. Vanuit $A$ komt de bij na een vlucht altijd op een van de twee middelste cellen terecht en moet ze daarna nog gemiddeld $x$ vluchten uitvoeren, dus $y = 1 + x$. Vanuit een van de middelste cellen komt ze met kans $1/3$ in $A$, met kans $1/3$ in $B$ en met kans $1/3$ in de andere middelste cel. Daarna moet ze nog $y$, $0$ en $x$ keer vliegen. Dus $x = 1 + 1/3y + 1/3 × 0 + 1/3x$, of $2x = 3 + y$. Uit de twee vergelijkingen volgt $y = 5$. De honingbij moet gemiddeld vijf vluchten uitvoeren om van $A$ naar $B$ te komen.

WaArheid En lEuGen

Noem een leugenaar $L$ en iemand die de waarheid spreekt $W$. Voor elk 3-voud rond de tafel is de volgende oplossing goed, waarbij de laatste $L$ naast de eerste $W$ zit:

$$WWLWWLWWL \dots WWLWWL.$$

Voor elk 3-voud - 1 is de volgende oplossing goed (laat de eerste $W$ in de vorige oplossing weg):

$$WLWWLWWL \dots WWLWWL.$$

Voor elk 3-voud + 1 is de volgende oplossing goed (zet een $L$ achter de eerste oplossing):

$$WWLWWLWWL \dots WWLWWLL.$$

Omdat elk getal geschreven kan worden als een 3-voud, een 3-voud - 1 of een 3-voud + 1, is er voor elk aantal personen groter dan of gelijk aan $5$ rond de tafel een oplossing.