We hebben gezien dat een mens een Light Up puzzel (of Akari zoals de puzzel internationaal heet) oplost door naar bepaalde lokale situaties te zoeken. Daarmee kan je steeds een paar kruisjes of lampjes plaatsen. Door die lampjes en kruisjes krijg je soms ook weer nieuwe situaties.

Je zou een computer ook naar dit soort lokale situaties kunnen laten zoeken. Het probleem is dat je hem maar een eindige lijst met situaties kan geven. Hierdoor kan hij niet elke puzzel oplossen, want voor elke eindige lijst met situaties die je algoritme kan herkennen, kan je een puzzel verzinnen waarin een situatie voorkomt die je algoritme niet kan herkennen. Je kan dit probleem oplossen met trial and error. Je zou je algoritme gewoon een lampje kunnen laten gokken als hij niets nieuws meer kan halen uit zijn lijst met situaties. Daarna laat je hem weer verder gaan met de situaties zoeken. Als hij hem op een gegeven moment oplost, ben je klaar, en als hij een tegenspraak tegenkomt weet hij dat het gegokte lampje een kruisje moest zijn, en dan kan je vanaf daar weer verder. Dit voelt alleen een beetje als een goedkope oplossing, en het ondermijnt het idee van een logische puzzel.

Om te zorgen dat ons algoritme toch elke puzzel op kan lossen, moesten we dus zorgen dat hij zelf een nieuwe situatie kan verzinnen waar afleidingen uit te halen zijn. Hiervoor hebben we het probleem geabstraheerd. Het blijkt dat je een Akari om kan zetten naar een aantal ongelijkheden. Een vakje met een lampje kan je waarde $1$ geven, en een vakje zonder lampje kan je waarde $0$ geven.

Dat hints een bepaald aantal lampjes om zich heen moeten hebben, laat zich dan vertalen in dat de waardes van de aangrenzende vakjes een bepaalde som moeten hebben (wat zowel een groter-dan-of-gelijk als een kleiner-dan-of-gelijk-ongelijkheid is).

Voor deze vergelijkingen schrijven we dus twee ongelijkheden in plaats van één gelijkheid. Dit is om praktische redenen, zodat het algoritme alleen maar met ongelijkheden hoeft te werken, in plaats van dat het onderscheid moet maken tussen ongelijkheden en gelijkheden. Dat elk vakje beschenen moet worden laat zich vertalen in dat de som van de waardes van alle vakjes die gezien worden door een vakje minstens $1$ moet zijn. En dat $2$ lampjes elkaar niet mogen beschijnen laat zich vertalen in dat de som van de waardes in een segment hoogstens $1$ is.

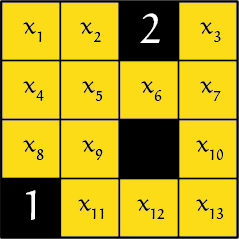In het bord hiernaast krijgen we zo bijvoorbeeld onder andere de volgende ongelijkheden:

$2 \le x_2 + x_3 + x_6 \le 2$,
$1 \le x_1 + x_4 + x_8 + x_9$ en
$x_2 + x_5 + x_9 + x_{11} \le 1$.

Omdat de $x_i$ alleen gelijk kunnen zijn aan $0$ of $1$, kunnen we in bepaalde situaties een $x_i$ bepalen op basis van zo’n ongelijkheid. Als bijvoorbeeld $a + b + 2c \ge 3$, dan weten we $c = 1$, want als $c = 0$, dan is de linkerkant hoogstens $2$. En als juist $a + b + 3c \le 2$, dan weet je $c = 0$, want anders is de linkerkant sowieso te groot.

We laten ons algoritme alle ongelijkheden afgaan om te kijken of hij bepaalde variabelen op deze manier kan forceren. Het is mogelijk dat geen enkele ongelijkheid meer nuttig is voordat de puzzel is opgelost. Met nuttig bedoelen we hier dat je een variabele kan forceren door alleen naar die ongelijkheid te kijken. Als geen enkele ongelijkheid meer nuttig is, dan laten we het algoritme elk tweetal ongelijkheden optellen. Dit komt overeen met bijvoorbeeld meerdere rijen naast elkaar bekijken, of twee hints die bij elkaar staan tegelijk bekijken. Hierdoor krijgen we nieuwe ongelijkheden die mogelijk wel nuttig zijn. De ongelijkheden $a + b \ge 1$ en $a + b + 3c \le 3$ zijn bijvoorbeeld elk afzonderlijk niet nuttig. Om ze op te tellen, moet het ongelijkheidsteken dezelfde kant op staan, dus we vermenigvuldigen de eerste met $-1$. Als we ze dan optellen, krijgen we $3c \le 2$, dus $c = 0$.

Door deze nieuwe ongelijkheden, kan het algoritme meestal weer nieuwe variabelen forceren. Hierdoor kunnen de oude ongelijkheden weer opnieuw nuttig worden. De ongelijkheid $a + b \ge 1$ is bijvoorbeeld niet meer nuttig, maar als we $a = 0$ weten door de nieuwe ongelijkheden, dan weten we door deze ongelijkheid ook $b = 1$. Zodra de nieuwe en de oude ongelijkheden allemaal opnieuw uitgeput zijn, telt het algoritme weer elk paar ongelijkheden bij elkaar op en gaat hij ze weer langs om te kijken of hij variabelen kan forceren. Dit herhaalt hij net zolang totdat de puzzel opgelost is.

ConClusie

Voor een computer en een mens is het anders om een Akari op te lossen. Als mens gaat het om patronen herkennen, en af en toe nieuwe patronen ontdekken. Een computer heeft deze visuele intuïtie niet. In plaats daarvan is een computer juist beter in abstract met nullen en enen werken, en gelukkig is het mogelijk om een Akari naar een abstract probleem te vertalen.

Je zou kunnen zeggen dat dit algoritme nog steeds trial and error is. Het algoritme telt namelijk elk paar ongelijkheden bij elkaar op in de hoop dat er een paar nuttige tussen zitten. Een intelligent algoritme zou kunnen voorspellen of het optellen van twee ongelijkheden wel of niet nuttig gaat zijn, en zou selectief ongelijkheden optellen in plaats van op goed geluk alle paren. Maar het algoritme hoeft geen nullen en enen te gokken, die kan hij wel met zekerheid afleiden. Dus al met al hebben we gezien dat abstractie een krachtig middel is om problemen op te lossen. Vooral voor computers is dit fijn, voor mensen kan een thematisch verhaaltje en visuele intuïtie ook nog nuttig zijn.

Via de knop [Bekijk oplossing] hieronder kom je op een pagina met een uitgewerkt voorbeeld en een link naar een Light-Up-Solver.

 

Bekijk oplossing