Wie ooit het vak optica heeft gehad is ongetwijfeld bekend met de lensformule. Die luidt als volgt:

$$\frac{1}{f}=\frac{1}{v}+\frac{1}{b}.$$

Hierin is $f$ de brandpuntsafstand van de lens, $v$ de afstand van een voorwerp tot de lens en $b$ de afstand van de lens tot het oppervlak waarop een beeld van het voorwerp wordt gevormd.

Nemen we bijvoorbeeld een positieve lens met een brandpuntsafstand van $30$ cm en plaatsen we een kaars links van de lens op een afstand van $50$ cm, dan zullen we op een afstand van $75$ cm rechts van de lens een scherp, omgekeerd beeld van de kaars zien als we daar een projectiescherm plaatsen (figuur 1).

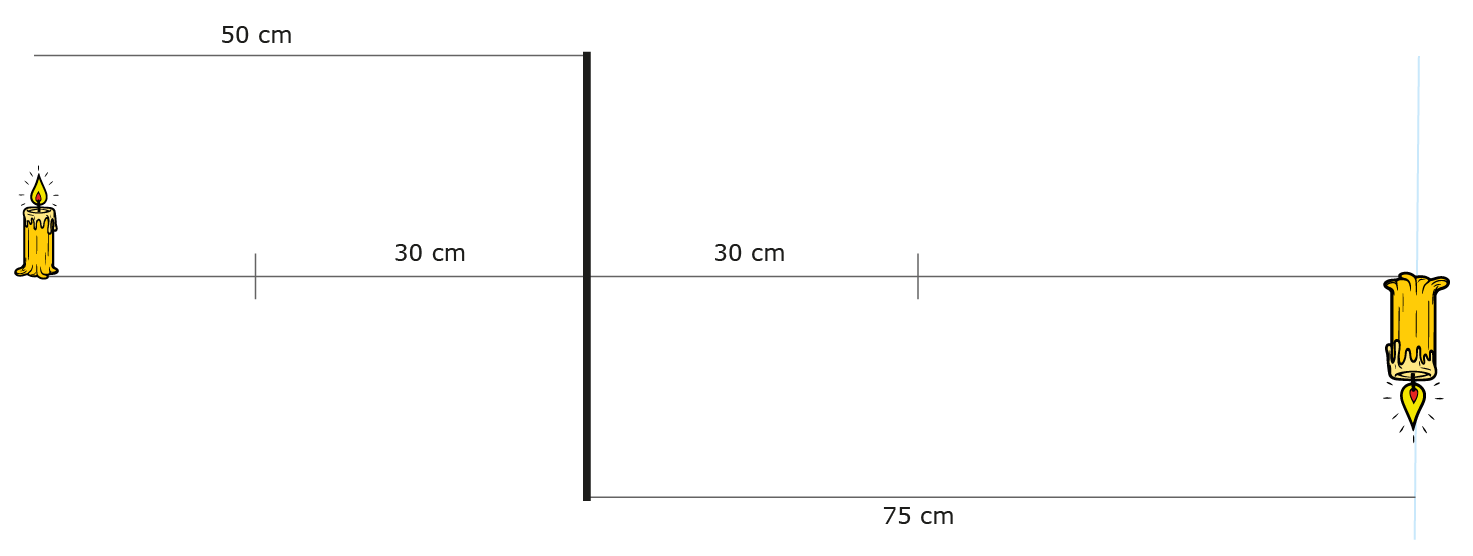
Stel dat we nu een lens hebben waarvan we de brandpuntsafstand niet weten. Die kunnen we dan vinden door de kaars op een zekere afstand van de lens te plaatsen en vervolgens het projectiescherm te verschuiven, net zolang tot we een scherp beeld van de kaars op het scherm zien. De voorwerpsafstand $v$ en $b$ kunnen we dan meten en met behulp van de lensformule kunnen we de brandpuntsafstand $f$ berekenen.

Nu geldt de lensformule alleen voor een ideale lens. Dat betekent onder andere dat we de dikte van de lens verwaarlozen. De afstanden $v$ en $b$ worden gemeten tot aan de verticale lijn die de lens voorstelt. In werkelijkheid hebben lenzen natuurlijk een zekere dikte. Bovendien hoeft een lens niet aan beide zijden dezelfde kromming te hebben zoals de lenzen in figuur 2 laten zien.

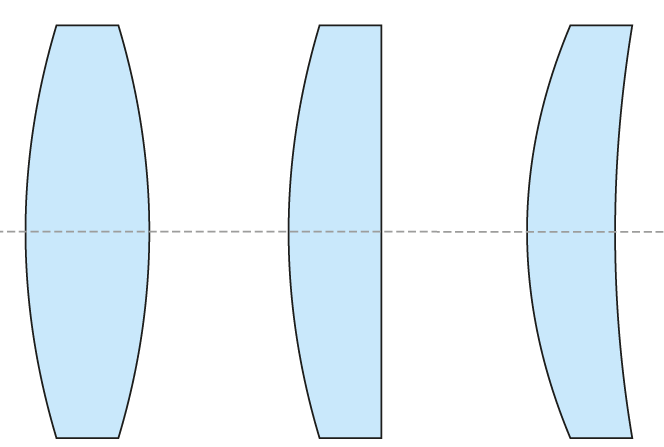
Dit heeft tot gevolg dat we de voorwerpsafstand $v$ en de beeldafstand $b$ niet exact kunnen bepalen. Ons meetlint kan immers maar tot het oppervlak van de lens komen, we kunnen niet verder in de lens meten waar het optisch centrum van de lens ligt om zo de exacte afstanden $v$ en $b$ te bepalen. Om dit probleem op te lossen bedacht de Duitse astronoom en wiskundige Friedrich Bessel in 1840 een slimme methode. 

Bessel was een veelzijdig wetenschapper. Hij heeft bijdragen geleverd aan de wiskunde, natuurkunde en sterrenkunde. Daarnaast was hij ook directeur van de Sterrenwacht van Königsberg, het huidige Kaliningrad. Daar was hij de eerste persoon die door middel van de parallaxmethode de afstand heeft kunnen bepalen naar een andere ster. Maar in dit artikel willen we de methode beschrijven die hij bedacht om de brandpuntsafstand van een lens te bepalen.

Als we weer kijken naar de afbeelding van de lens en de kaars hierboven dan zien we dat de kaars en het projectiescherm op een afstand van $50 + 75 = 125$ cm staan. Als we de kaars en het scherm laten staan maar nu de lens verschuiven, dan zullen we zien dat we weer een scherp beeld op het scherm hebben als de voorwerpsafstand $75$ cm is en de beeldafstand $50$ cm. Dat is natuurlijk geen verrassing. In de lensformule hoeven we alleen maar de waarden van $v$ en $b$ te verwisselen en dan zullen we weer een scherp beeld hebben. Als het scherm en de kaars op een vaste plek staan dan zijn er dus twee posities van de lens waarbij we een scherp beeld van de kaars op het scherm krijgen. Dit gegeven kunnen we ook gebruiken om de brandpuntsafstand van een dikke lens te bepalen.

We hebben een kaars en een scherm en die plaatsen we op een vaste afstand $L$ van elkaar. Vervolgens plaatsen we daartussen een lens waarvan we de brandpuntsafstand willen bepalen. We verschuiven de lens totdat we een scherp beeld zien. Dat gebeurt op zekere $v_1$ en $b_1$. Dan verschuiven we de lens totdat we weer een scherp beeld op het scherm zien. De daarbij horende waarden zijn dan $v_2$ en $b_2$. Nu kunnen we $v_1$, $b_1$, $v_2$ en $b_2$ niet meten vanwege de dikte van de lens. Maar we kunnen wel exact de afstand tussen de eerste en de tweede positie van de lens meten. Laten we die afstand $d$ noemen.

Wat nu volgt is een aardige vingeroefening in algebra. We weten

$\begin{align*}
v_1 &= b_2\\
v_2 &= b_1\\
v_2-v_1 &= d 
\end{align*}$

Hieruit volgt dat

$v_2-b_2=d.$

Uit de opstelling van kaars, projectiescherm en lens zien we dat

$v_2+b_2=L.$

Combineren van de laatste twee vergelijkingen geeft

$v_2=\tfrac{1}{2}(d+L)$

en

$b_2=\tfrac{1}{2}(L-d).$

Voor de tweede positie van de lens geldt

$\frac{1}{f}=\frac{1}{v_2}+\frac{1}{b_2}$

en met behulp van de uitdrukkingen voor $v_2$ en $b_2$ vinden we

$\frac{1}{f}=\frac{1}{\tfrac{1}{2}(d+L)}+\frac{1}{\tfrac{1}{2}(L-d)}$

waaruit volgt

$\frac{1}{f}=\frac{4L}{L^2-d^2}$

en uiteindelijk

$f=\tfrac{1}{4}L-\frac{d^2}{4L}.$

$L$ en $d$ zijn bekend dus hiermee hebben we de brandpuntsafstand $f$ berekend. Als we $f$ als functie van $d$ in een grafiek tekenen krijgen we een bergparabool (figuur 3).

Dit is de grafiek voor $L = 125$ cm, de waarde uit het voorbeeld aan het begin van dit artikel. De top ligt op , $f = \tfrac{1}{4}L= 31{,}25$. In dat geval geldt $d = 0$ dus dan is er maar één plaats voor de lens om een scherp beeld te krijgen. Dat is dan ook de maximale brandpuntsafstand die je kan meten voor een gegeven $L$.

Deze methode komt vooral van pas als we de brandpuntsafstand van een combinatie van lenzen willen bepalen. Bij een samenstellling van lenzen is het sowieso niet duidelijk wat de afstanden $v$ en $b$ zijn. Moet die afstand gemeten worden tot het oppervlak van de voorste lens, tot het meetkundige midden van de lenscombinatie, of iets anders? De methode van Bessel geeft ons de mogelijkheid om de lenscombinatie in gedachten te vervangen door een enkele lens met een effectieve brandpuntsafstand.

Tegenwoordig zijn er andere methoden om de brandpuntsafstand van een lenscombinatie te bepalen, maar in de 19^e en begin 20^e eeuw was Bessels methode de standaard in de optische werkplaatsen.