De 3×3-matrices in dit artikel hebben 3 rijen, 3 kolommen, 2 diagonalen en 9 cellen. In figuur 1 krijgen de drie soorten cellen in een 3×3-matrix verschillende kleuren. De middelste cel wordt rood, de 4 hoekcellen blauw en de 4 zijcellen geel.

De cellen worden vaak met getallen gevuld maar er zijn andere mogelijkheden. Denk eens aan het spel boter–kaas–en–eieren. Hier worden de cellen gevuld met 0-en en X-en door twee spelers die allebei proberen als eerste drie op een rij te krijgen.

Laten we, voordat we naar andere voorbeelden zoeken, afspreken dat we de cellen met alleen verschillende positieve hele getallen vullen. Daardoor vermijden wij gevallen zoals in figuur 2 en figuur 3.

Stel nu dat je de cellen wil vullen met de cijfers 1 tot en met 9 op zo’n manier dat de som in alle rijen, kolommen en diagonalen hetzelfde is. Als dit lukt dan heb je een magisch vierkant. Probeer het zelf voordat je verder gaat lezen.

Omdat de som van alle 9 cijfers 45 is en het vierkant bestaat uit drie rijen, moet de som van de getallen in iedere rij, kolom en op de diagonalen 15 zijn. De middelste cel moet op 4 manieren aangevuld kunnen worden tot 15 met andere cijfers. Het enige cijfer waarmee dit lukt is 5 en die moet dus in het midden. Het cijfer 1 moet in een zijcel want hij heeft slechts 2 aanvullingen. Dan moet de 9 in dezelfde lijn als de 1 en de 5. Nu komen de 6 en 8 aan weerszijden van de 1 en de rest is duidelijk. Afgezien van rotaties of spiegelingen is er maar één manier om deze 9 cijfers in te vullen. Ik noem dit het kleinste magische vierkant.

Voor degenen die al bekend zijn met killer sudoku’s zullen deze redeneringen wel bekend voorkomen. Als je die nog nooit hebt gemaakt, kun je ermee kennismaken op dailykillersudoku.com.

Er zijn oneindig veel magische vierkanten die we direct zouden kunnen genereren uit het kleinste voorbeeld boven.

Opgave 1

Hoe zou je magische vierkanten kunnen genereren op basis van het gegeven kleinste magische vierkant?

In het kleinste voorbeeld boven was de waarde 5 in de middelste cel een derde van de som 15 in alle rijen, kolommen en diagonalen.

Opgave 2

Laat zien dat deze verhouding van 1/3 geldt voor alle 3×3 magische vierkanten.

In het kleinste magische vierkant zijn twee sterke patronen te zien die met het gemiddelde van twee getallen te maken hebben.

Opgave 3

Wat zijn die patronen?

Opgave 4

Laat met behulp van de 1/3-regel zien dat deze patronen ook gelden in alle andere 3×3 magische vierkanten.

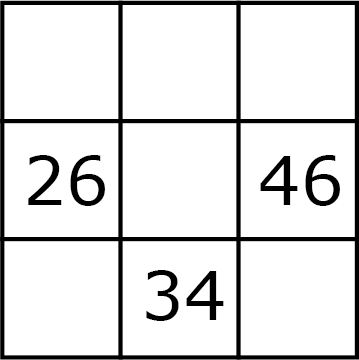
Nu kun je de matrix in figuur 4 afmaken als magisch vierkant. Dit magische vierkant is niet af te leiden uit het kleinste magische vierkant door bij alle cellen een constante op te tellen, of door alle cellen te vermenigvuldigen met een constante.

Opgave 5

Hoe kun je dat weten?

De operatie + is commutatief: (a + b) = (b + a), en associatief: (a + b) + c = a + (b + c). Dit maakt het eenvoudig om te praten over dé som in een rij, kolom of diagonaal. De operatie × heeft ook deze eigenschappen. Misschien is het mogelijk om magische 3×3 matrices te maken met de operatie × in plaats van +. Met behulp van machten kun je van een + magisch vierkant oneindig veel × magische vierkanten maken.

Opgave 6

Laat dat met een voorbeeld zien.

Opgave 7

Laat zien dat er analoge regels zijn voor alle 3×3 magische × vierkanten zoals de 1/3 regel en de twee gemiddelde regels voor + magische vierkanten.

Een matrix die begint zoals in figuur 5 kan tot een × magisch vierkant worden gemaakt, maar niet op basis van machten van één getal.

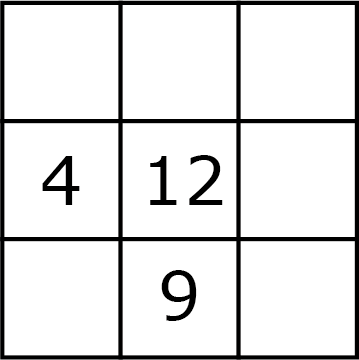
Opgave 8

Maak figuur 5 af als een × magisch vierkant.

Opgave 9

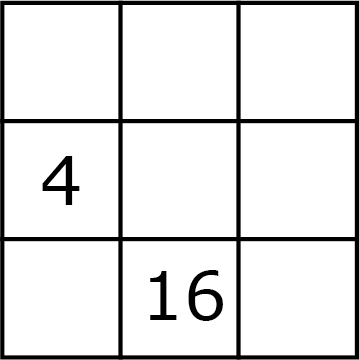
Laat zien dat de matrix die begonnen is in figuur 6 het begin kan zijn van oneindig veel + magische vierkanten maar ook het begin kan zijn van oneindig veel × magische vierkanten.