Opgave 1

Als je een constante optelt bij de waarden in alle cellen van een magisch vierkant dan is het nieuwe vierkant ook magisch. Hetzelfde geldt als je de waarden in alle cellen van een magisch vierkant vermenigvuldigt met een constante.

Opgave 2

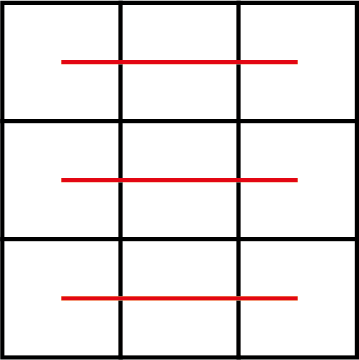
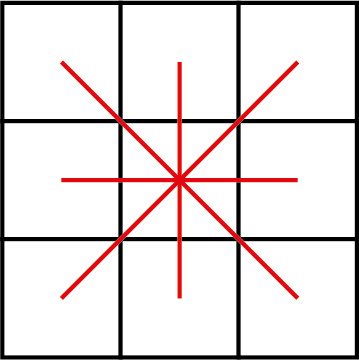
Uit de figuren 1 en 2 hieronder komt de vergelijking $3S = 4S - 3x$ waar $S$ de gemeenschappelijke som is en $x$ de waarde in de middelste cel.

Hieruit volgt dat $3x = S.$

Opgave 3

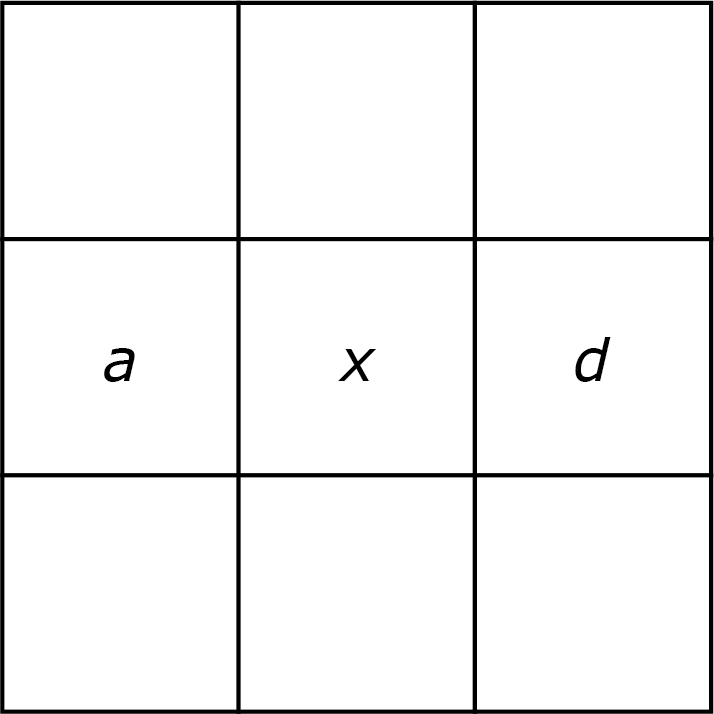
In figuur 3a zie je dat $\frac{a+d}{2}=x$ en alle vier lijnen door de middelste cel leveren een soortgelijke vergelijking.

In figuur 3b geldt $c=\frac{a+b}{2}.$ Deze relatie herhaalt zich ook vier keer.

Opgave 4

Van figuur 3a komt de vergelijking $a + x + d = 3x$ en dus $\frac{a+d}{2}=x.$ Van de rechterkolom in figuur 3b komt de vergelijking $c + (2x - a) + (x + c - b) = 3x$ en dus $c=\frac{a+b}{2}.$

Opgave 5

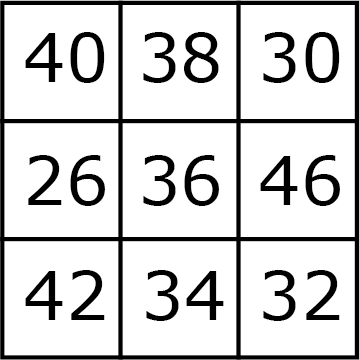
De waarden in de cellen vormen geen rij van getallen met onderling gelijke afstanden.

Opgave 6

Bijvoorbeeld:

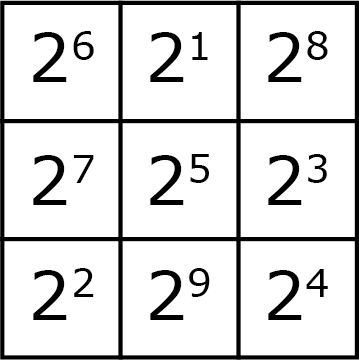
Opgave 7

Noem het gemeenschappelijke product $P.$ Dan komt uit figuur 1 en figuur 2 de vergelijking $P^3=\frac{P^4}{x^3}.$ Hieruit volgt dat $x^3 = P.$

In figuur 4a geldt $adx = x^3$ en dus $x=\sqrt{ad}.$

Figuur 4b geeft ons de vergelijking $\frac{c^2x^2}{ab}=x^3,$ dus $c=\sqrt{ab}.$

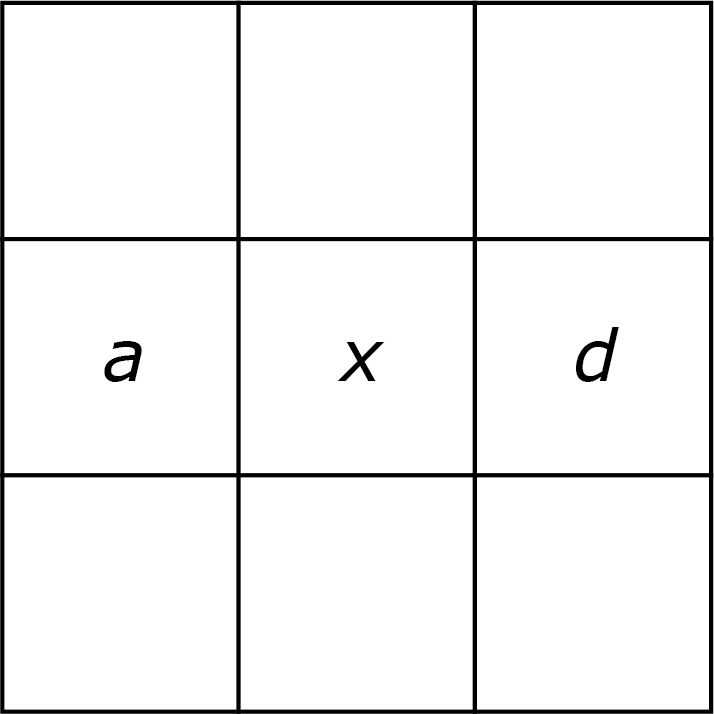
Opgave 8

Met behulp van de regels uit opgave 7 krijgen we het vierkant zoals in de onderstaande figuur.

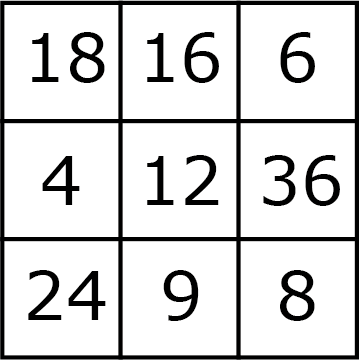
Opgave 9

De oplossingen voor de + magische vierkanten komen uit figuur 5a met alle $x$-waarden groter dan 8 behalve 10, 13, 16 en 22.

De oplossingen voor de × magische vierkanten komen uit figuur 5b met als $x$-waarden alle veelvouden van 4 groter dan 8 behalve 16 en 32.