We beginnen hier met affiene meetkunde. Dit is een meetkunde waarin de oorsprong 'is vergeten' (dit klinkt niet zo exact, maar de Franse meetkundige Marcel Berger vatte het zo samen). Hoewel we in de wiskunde op school gewend zijn te rekenen met coördinaten ten opzichte van een oorsprong en loodrecht op elkaar staande assen met dezelfde lengtemaat, is er noch in de werkelijke wereld noch in virtuele werelden in computerspelen een speciaal punt en een natuurlijk assenstelsel. Laten we eens onderzoeken hoe we in het vlak los kunnen komen van een willekeurig gekozen referentiepunt en coördinatenstelsel. Op het rooster in figuur 1 zijn twee verschillende oorsprongen of gezichtspunten $O$ en $Q$ aangegeven om punten te beschrijven. Ten opzichte van $O$ is $A = (4,2), B = (1,5)$ en ten opzichte van $Q$ is $A = (8,-1), B = (5,2)$. Als je de coördinaten optelt geldt vanuit $O$ gezien $A + B = (5,7), B - A = (-3,3)$ en vanuit $Q$ geldt $A + B = (13,1), B - A = (-3,3)$. Voor $A + B$ vinden we verschillende getallenparen, terwijl $B - A$ een eenduidige uitkomst heeft.

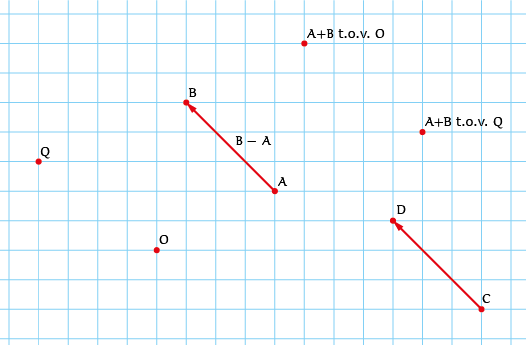
Deze vingeroefening leert ons dat als we de oorsprong willen vergeten, het verschil tussen punten belangrijk is. Dit verschil kan worden voorgesteld door een vector, een gericht lijnstuk of pijl van het ene naar het andere punt. De affiene ruimte bestaat uit punten en vectoren. We noteren de vector van punt $A$ naar punt $B$ als $B - A = \overrightarrow{AB}$.

Punten hebben een vaste plaats, maar vectoren niet. Bijvoorbeeld in figuur 1 geldt $\overrightarrow{AB}=\overrightarrow{CD}$. Een punt plus een vector geeft een ander punt: $B = A + \overrightarrow{AB}$. Maar punten kunnen niet worden opgeteld. Er is wel de mogelijkheid in een punt vectoren staart aan kop te leggen, met als hun som de diagonaal van het parallellogram dat ze opspannen. Dit geeft bijvoorbeeld $\overrightarrow{OA}+\overrightarrow{AB}=\overrightarrow{OB}$.

En we mogen vectoren schalen met een factor. Dit betekent dat vanuit $A$ een ander punt $X$ op dezelfde lijn als $A$ en $B$ kan worden bereikt door de vector $\overrightarrow{AB}$ met een factor $\lambda$ te vermenigvuldigen: $X=A+\lambda\cdot\overrightarrow{AB}$; $\lambda$ is de verhouding tussen $\overrightarrow{AX}$ en $\overrightarrow{AB}$. In het bijzonder is het midden $M$ tussen de punten $A$ en $B$ dus te schrijven als $M = A+\tfrac{1}{2}\overrightarrow{AB}$.

Beschouwen we $M$ zowel vanuit $O$ als vanuit $Q$, dan ontdekken we iets opvallends:

$\begin{align*}
M &= O + \overrightarrow{OA}+\tfrac{1}{2}\overrightarrow{AB}=O+\overrightarrow{OA}+\tfrac{1}{2}\left(\overrightarrow{OB}-\overrightarrow{OA}\right)=O+\tfrac{1}{2}\overrightarrow{OA}+\tfrac{1}{2}\overrightarrow{OB}\\
&=O+\tfrac{1}{2}\left(\overrightarrow{OQ}+\overrightarrow{QA}\right)+\tfrac{1}{2}\left(\overrightarrow{OQ}+\overrightarrow{QB}\right)\\
&=O+\overrightarrow{OQ}+\tfrac{1}{2}\overrightarrow{QA}+\tfrac{1}{2}\overrightarrow{QB}=Q+\tfrac{1}{2}\overrightarrow{QA}+\tfrac{1}{2}\overrightarrow{QB}.
\end{align*}$

Vanuit $O$ en $Q$ heeft de vector naar $M$ uitgedrukt in de vectoren naar $A$ en $B$ dezelfde coëfficiënten, namelijk ½ respectievelijk ½.

Opgave Ga na dat meer algemeen geldt: $O + \lambda\cdot\overrightarrow{OA} + (1-\lambda)\cdot\overrightarrow{OB} = Q + \lambda\cdot\overrightarrow{QA} + (1-\lambda)\cdot\overrightarrow{QB}$.

Dus als de coëfficiënten van de vectoren naar $A$ en $B$ optellen tot $1$, dan kom je vanuit $O$ en $Q$ op hetzelfde punt uit. En daarmee is de beschrijving van dat punt vanuit elk gezichtspunt in die zin gelijk en doet de keuze van de oorsprong er niet toe. En dat is juist wat we wilden bereiken. 

Opgave Ga na dat hetzelfde geldt voor drie punten $A$, $B$, $C$ en coëfficiënten $\kappa$, $\lambda$ en $\mu$, waarbij $\kappa + \lambda + \mu = 1$.

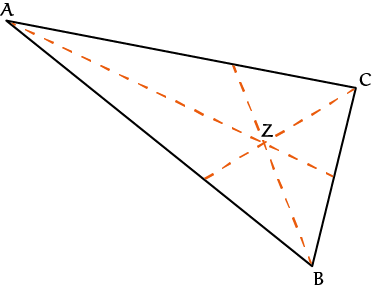
Het punt $Z=O+\kappa\cdot\overrightarrow{OA} +\lambda\cdot\overrightarrow{OB} +\mu\cdot\overrightarrow{OC}$ in figuur 2 hangt voor een gegeven driehoek en gegeven coëfficiënten dus niet af van de keuze van $O$. Om beter te begrijpen wat dit punt voor gegeven $0 < \kappa, \lambda < 1$ kan voorstellen, gaan we iets slims doen. We kiezen $O = Z$. Dan volgt uit $Z=Z +\kappa\cdot\overrightarrow{ZA}+\lambda\cdot\overrightarrow{ZB}+\mu\cdot\overrightarrow{ZC}$ dat $\kappa\cdot\overrightarrow{ZA}+\lambda\cdot\overrightarrow{ZB}+\mu\cdot\overrightarrow{ZC}=\overrightarrow{0}$, de nulvector.

Hieraan kunnen we een natuurkundige duiding geven. Beschouw drie puntmassa's $m_a, m_b, m_c$. Ze vormen een driehoek $ABC$. Nemen we $\kappa=\frac{m_a}{m_a+m_b+m_c}$, $\lambda=\frac{m_b}{m_a+m_b+m_c}$, $\mu=\frac{m_c}{m_a+m_b+m_c}$, dan is $Z$ het zwaartepunt van de drie puntmassa's. Immers, de som van de vectoren vanuit $Z$ gewogen met de overeenkomende (genormaliseerde) massa's is gelijk aan nul (met een natuurkundige benaming: de krachtmomenten ten opzichte van $Z$ heffen elkaar op). Een driehoekig plaatje met verwaarloosbare massa met in de hoeken de massa's is in evenwicht als je een potloodpunt onder $Z$ houdt.

Resteert nog het punt $Z$ aan te wijzen, opnieuw met een slimmigheidje. Kies $O = C$. De lijn door $C$ en $Z=C+\kappa\cdot\overrightarrow{CA}+\lambda\cdot \overrightarrow{CB}$ snijdt de zijde tegenover $C$ in het punt $C+\frac{\kappa}{1-\mu}\cdot\overrightarrow{CA}+\frac{\lambda}{1-\mu}\cdot\overrightarrow{CB}$. Dit snijpunt verdeelt de zijde volgens de verhouding $\kappa:\lambda=m_a:m_b$. Evenzo voor de andere hoekpunten. De ligging van het zwaartepunt van drie massa's kun je dus bepalen door de verhoudingen tussen de puntmassa's af te zetten op hun onderlinge verbindingslijnen. Hiervoor zijn geen oorsprong, coördinaten of goniometrie nodig.

Affiene meetkunde is de studie van meetkundige eigenschappen van figuren die bewaard blijven onder affiene afbeeldingen. In het vlak zijn dit alle afbeeldingen die een rooster van gelijke parallellogrammen overvoeren in een willekeuring ander rooster van (andere) gelijke parallellogrammen, te weten verschuivingen, afschuivingen, schalingen, draaiingen, spiegelingen en samenstellingen ervan. Ze verbinden verwante (Latijn: affinis) werelden. Lijnen gaan over in lijnen. Parallelle lijnen gaan over in parallelle lijnen. De verhoudingen tussen de onderlinge afstanden tussen drie punten die op dezelfde lijn liggen blijven behouden, maar in het meten van afstanden is niet voorzien. Afstanden en hoeken blijven in het algemeen niet behouden en zijn dan ook geen begrippen die in de affiene meetkunde worden gehanteerd. Toch volstaat de affiene meetkunde voor het bewijzen van allerlei stellingen.

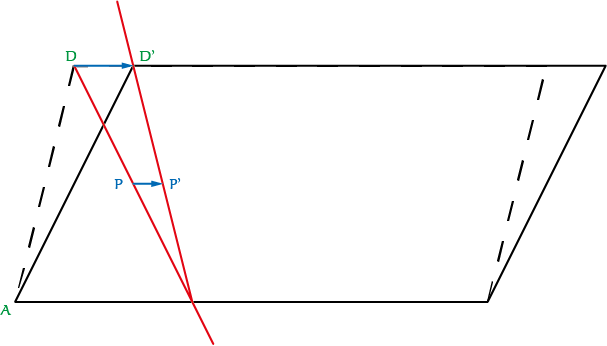
Van de genoemde afbeeldingen zijn afschuivingen misschien minder bekend. Een afschuiving ten opzichte van een bepaalde lijn verschuift elk punt in de richting evenwijdig aan die lijn over een afstand evenredig aan zijn afstand tot die lijn (met inachtneming van teken). In figuur 3 verandert een parallellogram door een afschuiving in een ander parallellogram (dat dezelfde hoogte heeft). Afschuiving kan ook zonder afstandsbegrip worden gedefinieerd, dus binnen de affiene meetkunde. De figuur toont dit als een 'constructie zonder woorden'.

Opgave Probeer te begrijpen hoe een punt $P$ afschuift naar $P'$. Tip: Er is niet meer gegeven dan de drie punten $A, D, D'$, en bedenk dat je een lijn kunt trekken met dezelfde richting als een andere lijn.

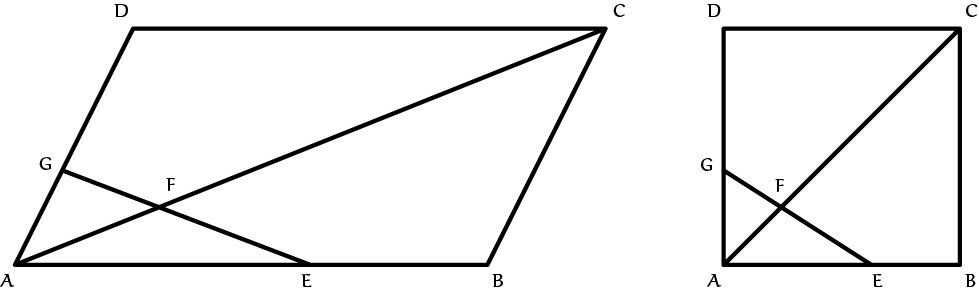
In figuur 4 doorsnijdt een lijn een parallellogram. De snijpunten verdelen twee van de zijden en de diagonaal elk in twee stukken in lengteverhoudingen die voldoen aan:

$$\frac{AB}{AE}+\frac{AD}{AG}=\frac{AC}{AF}$$

$(\star)$

Let wel, dit zijn verhoudingen tussen lijnstukken op dezelfde lijn. Zoals gezegd kent de affiene ruimte verhoudingen tussen gelijkgerichte lijnstukken, maar het is niet mogelijk lengten te meten en lijnstukken te vergelijken die niet in lijn liggen. Dit lijkt vreemd, maar veel wiskundige theorieën beogen met beperkte uitgangspunten een strak verhaal met krachtige stellingen te zijn en niet een onbestemde brij waarin van alles door elkaar loopt. Straks maken we nog een uitstapje naar de 'gewone', Euclidische meetkunde waarin meer kan.

We bewijzen $(\star)$ eerst met een berekening. In het parallellogram geldt:

$\begin{align*}
C&=A+\tfrac{AC}{AF}\cdot\overrightarrow{AF}=A+\tfrac{AC}{AF}\left(\overrightarrow{AE}+\overrightarrow{EF}\right)\\
&=A+\tfrac{AC}{AF}\left(\overrightarrow{AE}+\tfrac{EF}{EG}\cdot \overrightarrow{EG}\right)=A+\tfrac{AC}{AF}\left(\overrightarrow{AE}+\tfrac{EF}{EG}\left(\overrightarrow{AG}-\overrightarrow{AE}\right)\right)\\
&=A+\tfrac{AC}{AF}\left(1-\tfrac{EF}{EG}\right)\overrightarrow{AE}+\tfrac{AC}{AF}\tfrac{EF}{EG}\cdot\overrightarrow{AG},
\end{align*}$

maar ook:

$C=A+\overrightarrow{AB}+\overrightarrow{BC}=A+\overrightarrow{AB}+\overrightarrow{AD}=A+\tfrac{AB}{AE}\cdot \overrightarrow{AE}+\tfrac{AD}{AG}\cdot \overrightarrow{AG}$.

Opgave Reken na dat $(\star)$ volgt uit het gelijkstellen van de bovenstaande twee uitdrukkingen voor $C$.

Er is ook een ander bewijs voor $(\star)$. Wie bekend is met affiene meetkunde kan daarmee de opgave omzetten in een vorm die gemakkelijker op te lossen is. Vervorm het parallellogram tot een vierkant via een afschuiving en een schaling. Omdat dit affiene afbeeldingen zijn, beelden ze de lijn af op een lijn en handhaven ze de genoemde verhoudingen. In het vierkant kunnen we gemakkelijker rekenen dan in het parallellogram. Bijna ongemerkt zijn we in de 'gewone', Euclidische meetkunde terecht gekomen. We kunnen immers alleen spreken van een vierkant als we de begrippen afstand en hoek tot onze beschikking hebben!

Opgave Bewijs dat in het vierkant $(\star)$ geldt.  Tip: Neem het eenheidsvierkant, $AB = AD = 1$, $AC = \sqrt{2}$, beschrijf de lijn in coördinaten (neem $O = A$) en bedenk dat het punt $F$ op de diagonaal van het vierkant ligt.)

Dit is een eenvoudige toepassing, maar er zijn er ook die verrassender zijn. Sommige affiene stellingen waren al in de klassieke oudheid bekend. Tegenwoordig, zo'n twee millennia later, wordt affiene meetkunde gebruikt in technieken achter computer graphics en computer aided design, waar veel draait om het verplaatsen en vervormen van personages of voorwerpen, wat je wellicht spannender vindt dan het bestuderen van eigenschappen van eenvoudige figuren. Maar de eerste stap is een goed begrip van de beginselen, en daarvan hebben we er hier een aantal behandeld.