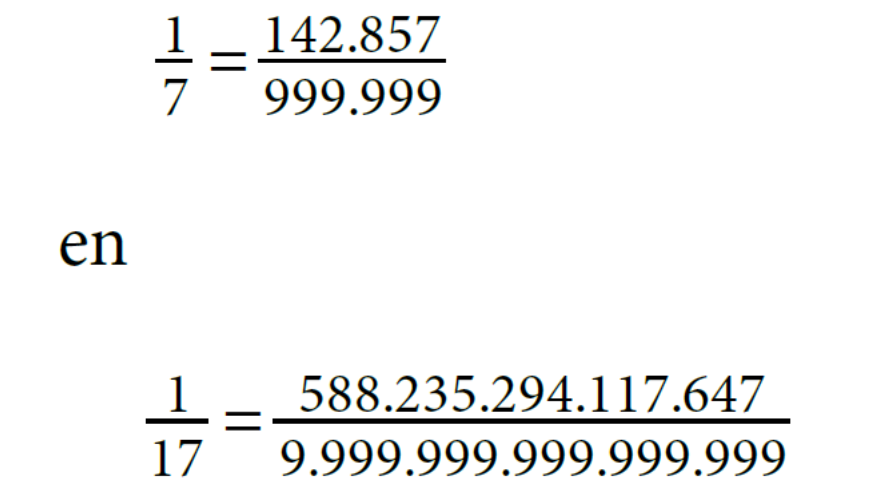
Megaperiodieke breuken maken
In november en januari heb je kunnen lezen over de ‘periode van een decimaal getal’. In dit artikel bekijken we wat er gebeurt als we ‘periodieke breuken’ met elkaar vermenigvuldigen. Breuken (uitgeschreven als decimaal getal) waarvan de periode erg groot is, bijvoorbeeld duizend of zelfs een miljoen, blijken verrassend simpel te construeren, uit kleine priemgetallen.
Als je de breuk $\frac{1}{7}$ schrijft als decimaal getal, krijg je $0,\overline{142857}$. De streep boven het groepje van zes cijfers betekent dat dit groepje eindeloos herhaald wordt. We zeggen: de periode van $\frac{1}{7}$ is gelijk aan 6.
In het artikel ‘De periode van een decimaal getal’ in het januarinummer stelden we zonder bewijs:
Kies twee priemgetallen a en b. Als hun omgekeerden $\frac{1}{a}$ en $\frac{1}{b}$, decimaal uitgeschreven, periode $p_a$ en $p_b$ hebben, dan heeft het product $\frac{1}{ab}$ periode $kgv(p_a, p_b)$. Hierbij staat kgv voor ‘kleinste gemene veelvoud’.
Met behulp van de 9-getallen uit het vorige artikel is het bewijs simpel. We geven het aan de hand van een voorbeeld, namelijk a = 7 en b = 17. We zeiden al dat $\frac{1}{7}$ periode 6 heeft. Verder heeft $\frac{1}{17} =0,\overline{0588235294117647}$ periode 16. Dus de breuk $\frac{1}{7}·17 = \frac{1}{119}$ zou, decimaal uitgeschreven, periode kgv(6, 16) = 48 moeten hebben.
Eerder bewezen we, dat elke periodieke breuk te schrijven is als een breuk met een 9-getal als noemer:
$$0,\overline{142857} = \frac{142.857}{999.999}$$
en
$$0,\overline{0588235294117647} = \frac{(0)588.235.294.117.647}{9.999.999.999.999.999} .$$
Je ziet: het aantal negens in de noemer is gelijk aan de periode van het decimale getal.
Uiteraard moet gelden:
$$\frac{1}{7}= \frac{142.857}{999.999}$$
en
$$\frac{1}{17} = \frac{588.235.294.117.647}{9.999.999.999.999.999}$$
en dat klopt, want 7 $\times$ 142857 = 999.999 en 17 $\times$ 588.235.294.117.647 = 9.999.999.999.999.999.
In feite bepaalt dit de periode van een breuk (uitgeschreven als decimaal getal): 999.999 is het kleinste 9-getal met een factor 7, en het kleinste 9-getal met een factor 17 is 9.999.999.999.999.999.
De schrijfwijze van een periodieke breuk als gewone breuk met een 9-getal in de noemer legt nu de volgende eis op:
(*) Voor $\frac{1}{7}·17$ (het product van 17 en $\frac{1}{17}$ ) hebben we een 9-getal in de noemer nodig met zowel een factor 7 als een factor 17, opdat we kunnen schrijven: $$\frac{1}{119} = \frac{1}{7·17} = \frac{\text{een of ander geheel getal}}{\text{9-getal met factor 7 en factor 17}}.$$
Nu gebruiken we twee eigenschappen van 9-getallen die we ook al eerder bewezen:
- een 9-getal van P – 1 cijfers heeft minstens één factor P (mits P niet 2 of 5 is);
- als het 9-getal met N cijfers het kleinste 9-getal is dat P als factor heeft, dan hebben enkel de 9-getallen met N, 2N, 3N, … cijfers één of meer factoren P.
Toegepast op het voorbeeld betekent dit, dat we van tevoren al wisten dat 999.999 een factor 7 moet bevatten, en 9.999.999.999.999.999 een factor 17. Hoe maken we hieruit een 9-getal dat zowel een factor 7 als een factor 17 bevat? Simpel: wegens de tweede eigenschap bevatten alle 9-getallen met 6, 12, 18, ... cijfers een factor 7, en alle 9-getallen met 16, 32, ... cijfers bevatten een factor 17. Het kleinste 9-getal dat in beide rijtjes voorkomt, is het 9-getal met aantal cijfers kgv(6, 16) = 48. Volgens de tweede eigenschap zijn deze twee rijtjes ook de enige 9-getallen met factoren respectievelijk 7 en 17, dus is het 9-getal met 48 cijfers ook echt de kleinste mogelijkheid.
Dit betekent dat de breuk $\frac{1}{119}$ te schrijven is als
$$\frac{\text{een of ander geheel getal van 48 cijfers}}{\text{9-getal met 48 cijfers}} .$$
Decimaal uitgeschreven is dit een breuk met periode 48, namelijk
$$\frac{1}{119} =0,\overline{008403361344537815126050420168067226890756302521}.$$
KWADRATISCHE STAMBREUKEN
Als a = b kan deze regel niet kloppen, immers, kgv(a, a) = a. We keren terug naar de eis, geformuleerd bij (*), maar vertaald naar het geval a = b, met a = 7 als voorbeeld:
(*) Voor $\frac{1}{7·7}$ hebben we een 9-getal in de noemer nodig met twee factoren 7, opdat we kunnen schrijven: $\frac{1}{49} = \frac{1}{7·7} = \frac{\text{een of ander geheel getal}}{\text{9-getal met twee factoren 7}}.$
We weten al dat $\frac{1}{7}$ periode 6 heeft, dus de 9-getallen met 6, 12, 18, ... cijfers hebben allemaal een factor 7. Maar wanneer komt daar een tweede factor 7 bij? Algemeen: als het kleinste 9-getal met een factor P een lengte van N cijfers heeft (10$^N$ – 1), wat is dan het kleinste 9-getal met een factor P$^2$?
Omdat $10^N – 1$ een factor P heeft, is het een of ander veelvoud V van P, dus kunnen we schrijven:
$$10^N – 1 = VP,$$
dus
$$10^N = VP + 1,$$
dus
$$10^{PN} = (10^N)^P = (VP + 1)^P.$$
Schrijf dit vervolgens uit met behulp van het binomium van Newton, $(a + b)^M$:
$$(VP + 1)^P = (VP)^P + P · (VP)^P – 1 + ... + P(P – 1) · (VP)^2 + P · (VP) + 1.$$
We hebben nu:
$$10^{PN} – 1 = (VP)^P + P · (VP)^{P – 1} + ... + P(P – 1) · (VP)^2 + P · (VP).$$
Alle termen aan de rechterkant bevatten een factor P$^2$, dus is $10^{PN} – 1$ een 9-getal met PN cijfers, dat deelbaar is door P$^2$; precies waar we naar zochten.
Maar is $10^{PN} – 1$ het kleinste 9-getal met factor P$^2$? Stel dat er een kleiner 9-getal is dat al factor P$^2$ heeft. Dit 9-getal heeft dan de vorm $10^{AN} – 1$ (want alleen deze 9-getallen hebben één of meer factoren P) met A < P. Op dezelfde manier als in het vorige artikel gebeurde voor priemfactor P, kun je bewijzen dat dan uitsluitend de 9-getallen $10^{AN} – 1,10^{2AN} – 1, 10^{3AN} – 1$, ... één of meer factoren P$^2$ hebben. In het algemeen: enkel de 9-getallen $10^{QAN}– 1$, met Q = 1, 2, 3, ... bevatten factor P$^2$. Maar we hebben net bewezen, dat in ieder geval $10^{PN} – 1$ een factor P$^2$ heeft, dus die moet in die rij 9-getallen voorkomen. Kan dat?
Dat kan alleen als PN = QAN, dus als P = QA. Maar hier staat dat P het product van twee gehele getallen is, terwijl P een priemgetal is. Dit kan niet, dus is er geen kleiner 9-getal met factor P$^2$ dan $10^{PN} – 1$.
Terugkerend naar het voorbeeld met $\frac{1}{7}$: deze breuk heeft periode 6, dus de noemer is het 9-getal met zes cijfers, $10^6 – 1$. We willen er een factor 7 bij, dus P is 7, dus het eerste 9-getal met twee factoren 7 is $10^{6 · 7} – 1 = 10^{42} – 1$. De periode van $\frac{1}{7·7}$ zal dus 42 zijn. En inderdaad:
$$\frac{1}{49} =0,\overline{020408163265306122448979591836734693877551}.$$
STAMBREUKEN MET MEER DAN TWEE PRIEMFACTOREN
Voor kleine priemgetallen a is de periode van $\frac{1}{a}$ vaak gelijk aan het maximum, a – 1. Zo heeft $\frac{1}{7}$ periode 6 en $\frac{1}{17}$ periode 16. Het hoeft echter niet: $\frac{1}{13}$ heeft periode 6. Voor een groot priemgetal G kun je niet voorspellen of zijn omgekeerde 1/G de maximale periodelengte G – 1 haalt, maar het wordt steeds onwaarschijnlijker naarmate G groter wordt.
Immers, dit gebeurt alleen als G pas in het (G – 1)-de 9-getal voor het eerst als priemfactor optreedt. Bekijk als voorbeeld een G van ongeveer een miljoen. Dan heeft priemfactor G ongeveer een miljoen keer de kans gehad om eerder in de rij 9-getallen zijn debuut te maken. En hoe groter de 9-getallen worden, hoe groter die kans, omdat het aantal priemfactoren, gemiddeld, toeneemt naarmate het 9-getal groter is.
Dus als je een breuk wilt maken met vrij kleine getallen in de noemer, maar met een zo lang mogelijke periode, moet je een klein priemgetal P kiezen met de langst mogelijke periode P – 1. De breuk $1/(P^k)$ heeft dan periode $(P – 1) · P^{k–1}.$
Al het bovenstaande geldt ook voor breuken 1/(a · b · c · ...) met meer dan twee verschillende priemfactoren. Dan moet je het kleinste 9-getal vinden dat factoren a, b, c, ... bevat, en dat heeft $kgv(p_a, p_b, p_c, ...)$ cijfers.
Zo kunnen periodes snel oplopen. Bijvoorbeeld $\frac{1}{17·29·47} = \frac{1}{23.171}$ is een breuk met periode kgv(16, 28, 46) = 2.576.
Je kunt dit zelf controleren door de breuk uit te rekenen met een online rekenmachine voor grote getallen, bijvoorbeeld: https://defuse.ca/big-number-calculator.htm.
Deze – en veel andere rekenmachines – geeft geen cijfers achter de komma, dus zelfs een breuk als $\frac{1}{7}$ geeft antwoord 0. Maar daar kun je simpel onderuit: voor de breuk $\frac{1}{17·29·47}$ voer je in:
$$10^{10000}/(17*29*47)$$
en je ziet als antwoord:
$$431 573 950 196 366 ...$$
Je kunt controleren dat de eerste 2.576 cijfers echt de periode zijn, door met 'control F' (Windows) of 'cmd F' (Mac) op de pagina te zoeken naar de begincijfers, dus naar ‘431 573 950’ (vergeet de spaties niet). Je vindt dit blokje dan opnieuw na 2.576, 5.152 en 7.728 cijfers, maar nergens anders.
HET PRODUCT VAN WILLEKEURIGE PERIODIEKE BREUKEN
Tot slot bekijken we een nog algemener geval: neem twee willekeurige periodieke breuken, zoals $0,\overline{523}$ en $0,\overline{3054478}$, en vermenigvuldig die. Wat is de periodelengte van hun product? We schrijven weer
$$0,\overline{523}·0,\overline{3054478}= \frac{523}{999}·\frac{3.054.478}{9.999.999}$$
en we gaan op zoek naar een 9-getal zodanig dat
$$\frac{523}{999}· \frac{3.054.478}{9.999.999} = \frac{\text{een of ander geheel getal}}{\text{een of ander 9-getal}}.\ \ \ \ \ (**)
Let wel: het product van twee 9-getallen is nooit zelf een 9-getal (ga maar na: $(10^N – 1)(10^M – 1) = 10^{N+M} – 10^N – 10^M + 1$, en dit is niet te schrijven als $10^R – 1$ voor enige R). Anders hadden we simpelweg 999 $\times$ 9.999.999 kunnen uitrekenen, dat 9-getal in de noemer zetten, 523 $\times$ 3.054.478 in deteller, en klaar is Kees.
Om het 9-getal te vinden dat in de noemer moet komen, ontbinden we beide 9-getallen links van het =-teken in factoren:
$999 = 3^3 · 37$ en $9.999.999 = 3^2 · 239 · 4649.$
Om het product als een breuk met een 9-getal als noemer te kunnen schrijven, hebben we een 9-getal nodig met de factoren 3$^5$, 37, 239 en 4.649. In de lijst met ontbindingen van 9-getallen (zie pagina 25-26 in het januarinummer) zien we dat 239 en 4.649 voorkomen in de 9-getallen met 7 en 14 cijfers, dus ook in die met 21, 28, ... cijfers. 37 komt voor in de 9-getallen met 3, 6, 9, ... cijfers. Omdat kgv(3, 7) = 21, komen 239, 4.649 én 37 voor in de 9-getallen met 21, 42, 63, ... cijfers.
Met de factor 3 moeten we net iets anders redeneren, omdat die in beide noemers optreedt, vergelijkbaar met wat er gebeurt als je twee identieke stambreuken vermenigvuldigt. We zagen daar, dat als een 9-getal met N cijfers een factor P heeft, het 9-getal met NP cijfers een factor P$^2$ heeft. Daaruit volgt meteen, dat het 9-getal met NP$^2$ cijfers een factor P$^3$ heeft, enzovoort.
Alle 9-getallen zijn deelbaar door 9, dus hebben een factor 3$^2$. Dan hebben de 9-getallen met 3, 6, 9, ... cijfers een factor 3$^3$, de 9-getallen met 9, 18, 27, ... cijfers hebben een factor 3$^4$, en de 9-getallen met 27, 54, 81, ... cijfers hebben een factor $3^5$. Het kleinste 9-getal dat alle benodigde factoren, 3$^5$, 37, 239 en 4.649 bevat, heeft dus kgv(3, 7, 27) = 189 cijfers.
Bekijk nu weer uitdrukking (**). De noemer, het 9-getal met 189 cijfers, bevat de factoren 3$^5$, 37, 239, 4.649 en nog een stel andere die we symbolisch aanduiden met [overige]. De teller is het getal 523 · 3.054.478 · [overige]. Dus
$$\frac{523}{999} · \frac{3.054.478}{9.999.999} = \frac{523·3.054.478·[overige]}{35 ·37·239·4.649·[overige]};$$
[overige] bevat dus het minimum aan factoren dat nodig is om een getal met factoren 35, 37, 239 en 4.649 aan te vullen tot een 9-getal. Conclusie: het product van een decimale breuk met periode 3 en een decimale breuk met periode 7 heeft hoogstens periode 189.
Let op: we schrijven ‘hoogstens’, omdat je bij een willekeurige breuk met 999 in de noemer niet kan uitsluiten dat die nog te vereenvoudigen is tot een kleinere breuk, en idem voor een breuk met 9.999.999 in de noemer. Bijvoorbeeld: elk 9-getal is deelbaar door 9 (dus ook door 3) , dus als je de teller door 9 (of 3) kunt delen, is zo’n breuk te vereenvoudigen. Alle 9-getallen met een even aantal cijfers zijn deelbaar door 11, dus als je de teller door 11 kunt delen, vereenvoudigt dit de breuk ook. In dat geval hoeft het 9-getal in de noemer van het product van de twee periodieke breuken minder factoren te bevatten, en voldoet mogelijk al een kleiner 9-getal daaraan. Als je voor beide tellers priemgetallen kiest, sluit je dat uit en bereikt de periode het maximum.
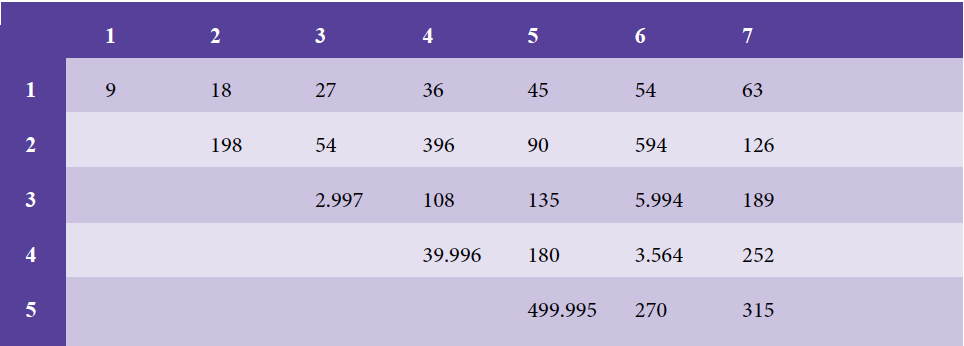
Zo kun je stuk voor stuk de maximale periode bepalen van producten van periodieke breuken met lengte 2, 3, 4, ... Dit is in de tabel onderaan de pagina samengevat. Uit deze tabel blijkt, dat het product van twee periodieke breuken met gelijke periode veel langere periodes oplevert dan een product van twee periodieke breuken met ongelijke periodes. Dat betekent bijvoorbeeld, dat als je twee priemgetallen van slechts drie cijfers kiest, zeg 359 en 617, het product $0,\overline{359}·0,\overline{617}$ periode 2.997 heeft.
Voor twee periodieke breuken met periode 5 kom je al uit op een maximale periode van 499.995, bijna een half miljoen! Priemgetallen van 5 cijfers zijn er zat, er staan lijstjes van op internet. De eerder genoemde online rekenmachine kan getallen tot een half miljoen cijfers aan, dus breuken met zulke enorme periodes kun je zelf maken.
Tot slot: de tabel suggereert dat de maximale lengte voor twee breuken met periode N gelijk is aan $N(10^N – 1)$. Of dit waar is voor alle N, laten we als open probleem aan de lezer...