Op de finale kwamen onder andere opgaven voorbij over getallen waarvan de delers zich bijzonder gedragen, geelrode kaartjes in een $4\times 4$-vierkant, en een sporttoernooi waarbij de gespeelde wedstrijden aan een bepaalde eigenschap voldoen (al deze opgaven zijn terug te vinden op www.wiskundeolympiade.nl in het Wedstrijdarchief). Opgave 3 ging over een kikker die met steeds grotere sprongen op een rooster rond aan het springen is. De vraag is vervolgens na hoeveel sprongen
hij weer terug op zijn beginpunt zou kunnen zijn. In het kader vind je de precieze opgave die de scholieren voor hun neus kregen.

Opgave 3, versie klas 6, finale 2021 Een kikker springt over de roosterpunten van een vlak, van het ene roosterpunt naar het andere. De kikker begint in het punt $(0, 0)$. Daarna maakt hij achtereenvolgens een sprong van $1$ stap horizontaal, een sprong van $2$ stappen verticaal, een sprong van $3$ stappen horizontaal, een sprong van $4$ stappen verticaal, en zo door. Bepaal alle $n > 0$ waarvoor de kikker na $n$ sprongen terug kan zijn in het punt $(0, 0)$.

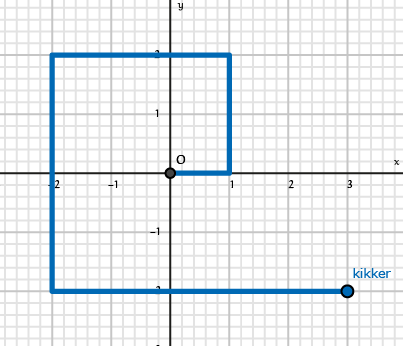
Hoe zou die kikker nu na $n$ sprongen terug kunnen zijn in de oorsprong? Een goed idee is om gewoon wat uit te proberen, door simpelweg een rooster te nemen en een aantal mogelijke kikkersprongen te tekenen. Als de kikker bijvoorbeeld $5$ sprongen ($n = 5$) allemaal tegen de klok in maakt, eindigt hij in het punt $(3 , -2)$, zie figuur 1.

We weten nu in elk geval dat de kikker in $5$ sprongen naar $(3, -2)$ kan springen. Alleen moest hij naar $(0, 0)$, dus daar hebben we niet zoveel aan. Waar komen $3$ en $-2$ uit dit eindpunt nu eigenlijk precies vandaan?

Wel, die $3$ is gelijk aan $1 - 3 + 5$ en die $-2$ komt van $2 - 4$. Als we voor alle horizontale sprongen het aantal stappen naar rechts optellen en hier het aantal stappen naar links van aftrekken, vinden we de
$x$-coördinaat van ons eindpunt. En natuurlijk geldt hetzelfde in de verticale richting, maar dan moeten we de sprongen omhoog optellen en daar alle sprongen omlaag vanaf halen. Hiermee zien we dat we, om de
opgave op te lossen, op zoek zijn naar alle $n$ zodanig dat we plussen en minnen kunnen vinden met $\pm1 \pm 3 \pm 5 \pm 7 \pm \cdots \pm m = 0$ en $\pm2 \pm 4 \pm 6 \pm \cdots \pm (m \pm 1) = 0$, waarbij $m$ het grootste oneven getal kleiner dan of gelijk aan $n$ is ($m \pm 1$ is het grootste even getal kleiner dan of gelijk aan $n$). De opgave valt hiermee eigenlijk uiteen in twee deelopgaven (de horizontale en de verticale richting), die we apart kunnen bekijken. Het lijkt nu misschien alsof we nog helemaal niet zoveel gedaan hebben. Immers, we hebben nog geen enkele n gevonden waarmee de kikker terug kan zijn in zijn beginpunt. Desondanks hebben we al wel degelijk iets erg belangrijks gedaan. Met onze observatie hebben we gevoel voor de opgave gekregen, en we hebben nu ruwweg een idee in welke richting we de oplossing moeten zoeken.

In horizontale riChting

Allereerst bekijken we of we kunnen vinden voor welke $m$ de som $\pm1 \pm 3 \pm 5 \pm 7 \pm \cdots \pm m$ gelijk kan zijn aan $0$. Ook nu is het weer handig om te beginnen gewoon wat uit te proberen. Kunnen we plussen en minnen vinden zodanig dat $\pm1 = 0$? Natuurlijk niet. Ook bij $\pm1 \pm 3$ is dit duidelijk onmogelijk, en na even puzzelen kom je erachter dat ook met $\pm1 \pm 3 \pm 5$ een $0$ als uitkomst onhaalbaar is. Wat trouwens wel opvalt bij dit puzzelen is dat bij deze laatste
alle resultaten oneven zijn. Vrij logisch, want drie oneven getallen optellen en/of aftrekken geeft altijd een oneven uitkomst. Aangezien $0$ even is, wisten we eigenlijk van tevoren al dat er sowieso geen oplossing mogelijk was. We zien hiermee, als $t$ het aantal termen in onze som is, dat het altijd onmogelijk is op $0$ uit te komen wanneer $t$ oneven is. We hebben dus al oneindig veel waardes van $n$ gevonden waarvoor het onmogelijk is voor de kikker om op de oorsprong terug te zijn! Alleen een $n$ waarvoor dit wel lukt hebben we nog steeds niet gevonden. Weer verder met wat kleine gevalletjes uitproberen dan maar.

We waren gebleven bij $\pm1 \pm 3 \pm 5 \pm 7$. Maar wacht eens, $1 - 3 - 5 + 7 = 0$. Dat is fijn: we hebben onze eerste oplossing voor de horizontale richting  gevonden. Laten we eens analyseren waarom we hier plussen en minnen hebben kunnen vinden om de som $0$ te maken. Dit komt omdat de som van het grootste en kleinste getal ($1 + 7$), gelijk is aan de som van de twee middelste getallen ($3 + 5$). Maar voor elke vier opeenvolgende oneven getallen geldt dat de som van de
grootste en de kleinste gelijk is aan de som van de twee middelste, en dus zijn voor vier opeenvolgende oneven getallen altijd plussen en minnen te vinden om hun som
op $0$ te krijgen. Dat kunnen we makkelijk bewijzen, als $p$ een oneven getal is, geldt dat $p - (p + 2) - (p + 4) + (p + 6) = p - p - 2 - p - 4 + p + 6 = 0$. Hierdoor vinden we bijvoorbeeld ook dat $(1 - 3 - 5 + 7) + (9 - 11 - 13 + 15) = 0 + 0 = 0$ en $(1 - 3 - 5 + 7) + (9 - 11 - 13 + 15) + (17 - 19 - 21 + 23) = 0 + 0 + 0 = 0$, etcetera. Oftewel: als $t$ (het aantal termen in onze som) deelbaar is door $4$ dan weten we zeker dat er plussen en minnen te vinden zijn zodanig dat de som $0$ wordt. Omdat we al hadden laten zien dat dit sowieso onmogelijk was als $t$ oneven is, hoeven we enkel nog de optie te onderzoeken dat $t$ wel even is, maar niet deelbaar door $4$.

Het eerstvolgende geval van deze vorm dat we nog niet bekeken hadden is $\pm1 \pm 3 \pm 5 \pm 7 \pm 9 \pm 11$. We zien dat $1 + 3 + 5 + 7 + 9 + 11 = 36$, dus de som van alle positieve termen in een eventuele oplossing zal de helft hiervan zijn, wat $18$ is. Kunnen we uit deze zes getallen er een aantal uitkiezen die samen een som van $18$ hebben? Ja, bijvoorbeeld $7$ en $11$. Hieruit volgt dat $-1 - 3 - 5 + 7 - 9 + 11$ gelijk is aan $0$, dus we hebben een oplossing. Vervolgens kunnen we voor elke vier extra termen weer het trucje toepassen dat voor vier opeenvolgende oneven getallen de som van de kleinste en de grootste gelijk is aan de som van de  middelste twee, om bijvoorbeeld $(-1 - 3 - 5 + 7 - 9 + 11) + (13 - 15 - 17 + 19) = 0 + 0 = 0$ te krijgen. Samenvattend hebben we dus gevonden dat er altijd plussen en minnen te vinden zijn om de som $0$ te maken als $t$ even is, behalve wanneer $t = 2$.

In verticale riChting

Dan nu het verticale geval. Dat lijkt erg veel op de opgave in horizontale richting, dus hopelijk kunnen we de daarvan geleerde technieken hier toepassen. Allereerst lieten we zien dat sommige waardes van n onmogelijk waren door te kijken wanneer de som oneven is. Dat wordt hier een beetje lastig; aangezien alle termen even zijn, krijgen we namelijk altijd een even uitkomst. Omdat alle termen even zijn, kunnen we echter alles delen door $2$. Dan kunnen we wel weer een argumentje op basis van even/oneven maken. We zijn dus op zoek naar wanneer er plussen en minnen te vinden zijn om $\pm 1 \pm 2 \pm 3 \pm 4 \pm \cdots \pm s$, met $s = \frac{m\pm 1}{2}$,
gelijk te krijgen aan $0$. Dit is in feite de opgave als de kikker alleen maar over een horizontale getallenlijn zou springen, wat als voorbereidend onderdeel aan de versie
voor klas 5 en lager toegevoegd was. We zien dat deze som altijd oneven is als het aantal oneven getallen kleiner dan of gelijk aan $s$ oneven is. Dat gebeurt precies als
$s$ van de vorm $4k + 1$ of $4k + 2$ is, voor zekere $k$ (het aantal oneven getallen kleiner dan $4k$ is even, en samen met het oneven getal $4k + 1$ is het totaal dus oneven). 

Dan hoeven we nu enkel te onderzoeken wat er gebeurt als s van de vorm $4k + 3$ of $4k$ is. Bij $\pm1 \pm 2 \pm 3$ is de oplossing $1 + 2 - 3 = 0$ snel  gevonden en ook bij $\pm1 \pm 2 \pm 3 \pm 4$ duurt het niet lang om te bedenken dat $1 - 2 - 3 + 4$ gelijk is aan $0$. Ook voor vier opeenvolgende gehele getallen geldt dat de som van de kleinste en de grootste gelijk is aan de som van de twee middelste, waardoor ieder extra viertal zichzelf weer kan uitschakelen (ga zelf na dat $p - (p + 1) - (p + 2) + (p + 3) = 0$). Zo krijgen we bijvoorbeeld $(1 + 2 - 3) + (4 - 5 - 6 + 7) = 0 + 0 = 0$ en $(1 - 2 - 3 + 4) + (5 - 6 - 7 + 8) = 0 + 0 = 0$. We zien dus dat hieruit direct een plus/
min-verdeling voortvloeit voor alle $s$ van de vorm $4k + 3$ of $4k$, waarmee we alle mogelijke vormen die $s$ zou kunnen aannemen hebben gehad.

Eindantwoord

In de horizontale richting hebben we geconcludeerd dat $t$ even moet zijn (behalve $t = 2$) en in de verticale richting zagen we dat $s$ van de vorm $4k + 3$ of $4k$ moet zijn. Herinner je dat $t$ het aantal oneven getallen kleiner dan of gelijk aan $n$ was. Als $t$ even is, betekent dit dus dat $n$ van de vorm $4j$ of $4j + 3$ is (er is een even aantal oneven getallen kleiner dan $4j$, en $4j + 1$ samen met $4j + 3$ maken dat ook als $n$ van de vorm 4j + 3 is, t even zal zijn). Als $n$ van de
vorm $4j$ is, betekent dit dat $n$ er ofwel als $8l$ ofwel als $8l + 4$ uitziet, en uit $4j + 3$ halen we dat $n$ de vorm $8l + 3$ of $8l + 7$ zal hebben. Verder was $s$ gelijk aan de helft van het grootste even getal kleiner dan of gelijk aan $n$, dus als $s$ van de vorm $4k + 3$ of $4k$ is, zal dit grootste even getal de vorm $8l + 6$ of $8l$ moeten hebben. Hieruit volgt dat $n$ enkel van de vorm $8l + 6$, $8l + 7$, $8l$ of $8l + 1$ kan zijn. 

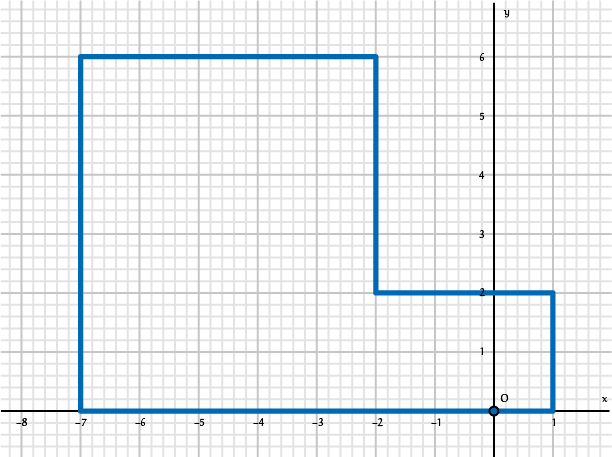
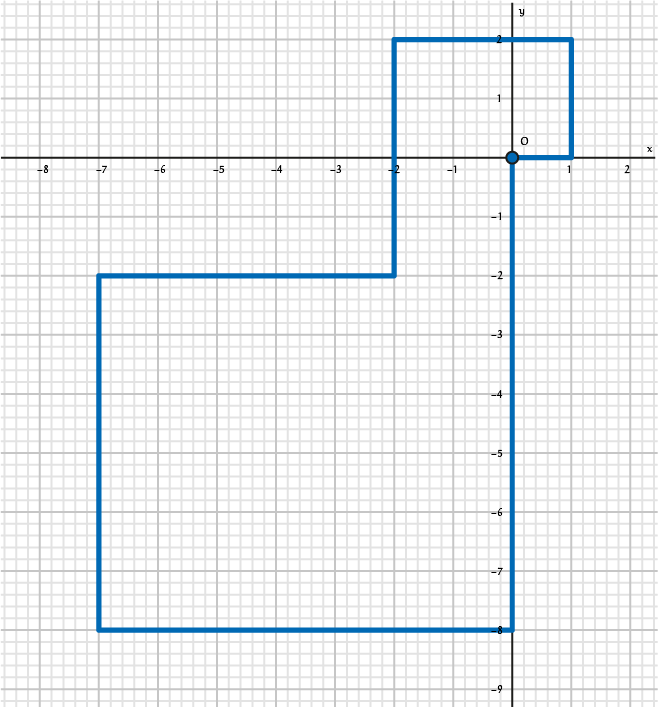
Deze observaties samenvoegen geeft dat $n$ de vorm $8l + 7$ of $8l$ zal moeten hebben. Verder hebben we in bovenstaande redenering ook al laten zien dat telkens wanneer $n$ inderdaad van de vorm $8l + 7$ of $8l$ is, de kikker zowel op de $x$-as als op de $y$-as terug zou kunnen zijn, en dus de oorsprong nogmaals een bezoekje zou kunnen brengen. In figuur 2 en 3 staan als voorbeeld de routes die de kikker kan afleggen als $n = 7$ en $n = 8$, om weer naar zijn beginpunt terug te keren. Nu we de opgave volledig opgelost hebben, moeten we ons gehele bewijs nog overzichtelijk in een netversie op schrijven, en dan maar hopen dat we de volle tien punten krijgen...

Terugblik

Dit was een vrij bijzondere opgave over een kikker die sprongen op een rooster maakt waar we eigenlijk niet zoveel vanaf weten. Immers, na $n$ sprongen zou de kikker al $2^n$ verschillende routes afgelegd kunnen hebben, en dan zouden wij moeten bepalen welke hiervan terug naar de oorsprong leiden. Zoals we zagen, is het bij zo'n vreemde opgave een goed idee je in eerste instantie niet zoveel te bekommeren over het gevraagde en maar eens te gaan experimenteren, zodat je een beter idee hebt wat van er aan de hand is. Daarnaast hebben we ook gezien dat het altijd erg verstandig is om een aantal kleine gevalletjes te bekijken en  grondig te analyseren, zodat duidelijk is welke bewijstechnieken je in het algemene geval zult moeten inzetten. In elk geval was dit een vrij pittige opgave. Dat bleek ook uit de statistieken: van de $10$ punten die je kon krijgen, hebben de zesdeklassers gemiddeld $3{,}4$ punten gescoord en de vijfdeklassers en lager kregen ongeveer $2{,}9$ punten gemiddeld.

Bij dit soort opgaven is er altijd een aantal variaties op de precieze weg die je naar de oplossing zou kunnen nemen. Zo hoefde je bijvoorbeeld niet te delen door $2$ in het verticale geval. In plaats daarvan had je een redenering over deelbaarheid door $4$ moeten maken. Als je trouwens de verticale richting eerst had gedaan (zoals de finalisten van klas 5 en lager sowieso moesten doen), werd de horizontale richting net een stukje makkelijker. Het was namelijk sowieso al uitgesloten dat $n$ van de vorm $8l + 3$ en $8l + 4$ zou kunnen zijn door het verticale geval, waardoor het argumentje dat we daar op het einde maakten eigenlijk niet nodig zou zijn geweest. Wat je in elk geval mee kunt nemen van deze uitwerking is de kracht van kleine doch belangrijke vorderingen. In feite is deze opgave slechts een aaneenschakeling van dit soort mini-succesjes, maar die moeten dan allemaal maar net lukken. Zoals wel vaker geldt: als je maar genoeg kleine stapjes zet, maak je binnen de kortste keren grote sprongen.